go to homepage
The Light Clock
In this short paper I will do a close analysis of the most current visualization of time dilation, which is the "light clock". This visualization is now included in most up-to-date explanations, since it appears to give the shortest road to the time transform. The diagram below of the light clock is the same in most respects to a diagram I used in my long paper on Special Relativity, which was a diagram of a spaceship passing the earth. In both diagrams we have the Pythagorean theorem used to find the third leg of a right triangle, and this equation yields the dilated time. If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.
by Miles Mathis
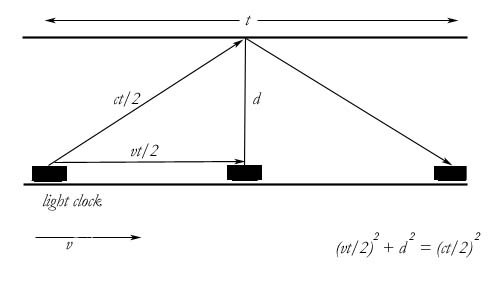
But like the spaceship diagram, this diagram creates a false visualization. A light clock works by emitting a light ray. This ray reflects from a mirror opposite the clock and returns. One round-trip of the light is a tick of the clock. The diagram is meant to be a visualization of what a distant observer would see. This distant observer sees the clock moving at velocity v. The diagram must be from the point of view of a distant observer, since a local observer would not see the clock moving. The clock itself could not possibly see itself moving, since it has no velocity relative to itself. But the creator of the diagram assumes the distant observer would see light moving as it is diagrammed. In fact, he would see nothing of the sort. A distant observer would not see the light at all. The light is moving perpendicular to his line of sight, and is invisible by definition. The vector ct/2 is imaginary. It cannot be anyone’s data. It is an assumption, and it is a false assumption. The light does not travel in that way, as I have shown and will show again below.
It is true that the time will be dilated for the distant observer, but not for the mathematical reason diagrammed here. The time will be dilated due to differences in the data we receive from the clock directly. To know what is going on with this light clock, the light clock must send us information in some way. Most of the time this information will arrive on light rays, whether it is visual or not. It is these light rays that actually come to us that we must do the transforms with.
In the light clock diagram, the creator of the diagram has shown us three separate positions of the clock. If we assume that the third position is farther away from us—as distant observers—than the first position, then it must take light longer to reach us from that third position. This, by itself, will create time dilation, since the period of the clock will be stretched out.
The transforms of Relativity must be done on light rays that are part of our data. We cannot do transforms on imaginary light rays. Special Relativity applies to real data, to real observations, and cannot be applied to non-verifiable assumptions or imaginary vectors.
As further proof of this, let us analyze the diagram with a bit more depth. Notice that the clock in the first position needs to send the light ray off at an angle. How does the clock know which angle to send the light off at? You will say that we are using light that is emitted in all directions, so that some of that light will reach the clock at the third position. But what if we imagined a light clock that did not emit light in all directions. What if we assume a light clock that sends out a laser? Does the creator of this diagram mean to imply that if our clock sends out a laserbeam straight across to the far mirror, it will come back and miss the clock, since the clock will have moved on? Unlikely.
You may answer that the laserbeam emitted from the clock will act like a ball bounced by a boy on a bicycle. If a boy bounces a ball while riding a moving bicycle, the ball comes back to his hand. This is because the ball has a forward motion as well as a bouncing motion. If you answer this or assume this, you have broken Einstein’s Postulate 2. To paraphrase: “The speed of the light is independent of the motion of the source or the receiver.” The laser is emitted at speed c at one and only one angle. It cannot also have a forward motion. This forward motion would be a forward velocity, which would take its total velocity above c.
You may now answer, “OK, so the diagram has problems. But you yourself admit that the laserbeam will end up at the third position. How else can you diagram it?” The answer is, you cannot diagram it properly. It is impossible to diagram three separate events on one piece of paper, especially when one of those events is light traveling in a foreign field. The false light vector is caused by trying to compress three events into one diagram. You end up getting a pretty good idea of how the sequence of events would look to a distant observer, but you get a very skewed idea of the way that light is traveling. This is because the light traveling is not an "event" to the distance observer. As I keep saying, that vector is invisible, it is not a possible part of his data. That vector exists only in a diagram like this, which is a compressed and false diagram. The real event is not taking place at a distance. The event of light traveling across to the mirror and back is a strictly local event. Light can be seen only where it is. It cannot be seen where it is not. Light cannot be seen at a distance. Therefore you cannot transform the light itself. You can only use the data given you by light to transform other things.
Einstein himself admitted this, and warned us of it. He told us that light is a special case. It is not an object like any other object. When we use light in Relativity, we must take special care not to make false assumptions. This is what Postulate 2 means: "Take care! Light is not just another object. It is emitted at velocity c from all objects, no matter how they are moving themselves. You may not add your velocity to the velocity of light, not if you are travelling in the same line as the light, and not if you are travelling at an angle to the emission."
This last bolded phrase should warn us that we cannot make the assumption the diagram above has made, which is that light can be emitted at different angles relative to different observers. It can't, because if it could this would imply that it had different resultant velocities. Just by drawing light in this way, you have set up a situation that cannot help but produce paradoxes. The bottom line is that you cannot draw or diagram or imagine "light at a distance." There is physically no such thing as light at a distance. Light is a local event and only a local event—this is what Postulate 2 means and must mean.
Therefore, the question, "where is the light right now?" is always a local question. If the light is in your eyes, you can say, "it is here." Otherwise, you can say nothing. You cannot propose to diagram light from a distance, since your diagram is supposed to be a diagram of your data. You cannot diagram light from a distance, since there is no such data. You know only the information that light brings you, and when you receive this information, the light is right in your eyes. Light in other fields is imaginary data, and if you try to diagram it you are sure to get into trouble. As a matter of data or of operation or of experience or of science, there is no such beast as "light in another field." Light is always in the local field. That is what Einstein's Second Postulate means.