return to homepage

A Disproof of Newton’s
Fundamental Lemmae

by Miles Mathis

First written November 2005

Newton published his Principia in 1687. Except for Einstein’s Relativity corrections, the bulk of the text has remained uncontested since then. It has been the backbone of trigonometry, calculus, and classical physics and, for the most part, still is. It is the fundamental text of kinematics, gravity, and many other subjects.
      In this paper I will show a simple and straightforward disproof of one of Newton’s first and most fundamental lemmae, a lemma that remains to this day the groundwork for calculus and trigonometry. My correction is important—despite the age of the text I am critiquing—due simply to the continuing importance of that text in modern mathematics and science. My correction clarifies the foundation of the calculus, a foundation that is, to this day, of great interest to pure mathematicians. In the past half-century prominent mathematicians like Abraham Robinson have continued to work on the foundation of the calculus (see Non-standard Analysis). Even at this late a date in history, important mathematical and analytical corrections must remain of interest, and a finding such as is contained in this paper is crucial to our understanding of the mathematics we have inherited. Nor has this correction ever been addressed in the historical modification of the calculus, by Cauchy or anyone else. Redefining the calculus based on limit considerations does nothing to affect the geometric or trigonometric analysis I will offer.
      The first lemma in question here is Lemma VI, from Book I, section I (“Of the Motion of Bodies”). In that lemma, Newton’s provides the diagram below, where AB is the chord, AD is the tangent and ACB is the arc. He tells us that if we let B approach A, the angle BAD must ultimately vanish. In modern language, he is telling us that the angle goes to zero at the limit.



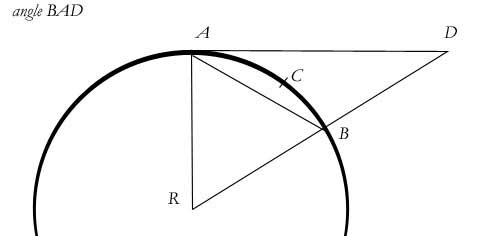
This is false for this reason: If we let B approach A, we must monitor the angle ABD, not the angle BAD. As B approaches A, the angle ABD approaches becoming a right angle. When B actually reaches A, the angle ABD will be a right angle. Therefore, the angle ABD can never be acute. Only if we imagined that B passed A could we imagine that the angle ABD would be acute. And even then the angle would not really be acute, since we would be in a sort of negative time interval. Newton is using A as his zero-point, so that we cannot truly cross that point without arriving in some sort of negative interval, especially since we are talking about the motion of real bodies.

[I have added this paragraph after talks with many readers, who cannot visualize the manipulation here. It is very simple: you must slide the entire line RBD toward A, keeping it straight always. This was the visualization of Newton, and I have not changed it here. I am not changing his physical postulates, I am analyzing his geometry with greater rigor than even he achieved. You may take this link, where his second animation is the correct one.]

If we are taking B to A and may not go past A, then the angle ABD has a limit at 90^o. When ABD is at 90^o, the angle BAD may not be zero. This will be crystal clear in a moment when we look at the length of the tangent at the limit, but for now it is enough to say that if angle BAD were zero, then ADB would also have to be 90^o, which is impossible to propose. A triangle may not have two angles of 90^o.

In Lemma VII, Newton’s uses the previous lemma to show that at the limit the tangent, the arc and the chord are all equal. I have just disproved this by showing that the angle ABD is 90^o at the limit. If ABD is 90^o at the limit, then the tangent must be greater than the chord. Please notice that if AB and AD are equal, then ABD must be less than 90^o. But I have shown that ABD cannot be less than 90^o. B would have to pass A, which would put us in a negative time interval. If B cannot pass A (A being the limit) then the tangent can never equal the chord, not when approaching the limit and not when at the limit.
      This verifies my previous assertion that the angle BAD cannot go to zero. If the tangent is longer than the chord at the limit, then this is just one more reason that the angle BAD must be greater than zero, even at the limit. If AD is greater than AB, then DB must be greater than zero. If DB is greater than zero, then the angle BAD is greater than zero.
      All this is caused by the fact that the angle ABD goes to 90^o before the angle BAD goes to zero. The angle ABD reaches the limit first, which keeps the angle BAD from reaching it. BAD never reaches zero.

Of course this means that B never reaches A. If B actually reached A, then we would no longer have a triangle. The tangent and the chord are equal only when they both equal zero, and they both equal zero when the interval between A and B is zero. But the 90^o angle at ABD prevents this from happening. When that angle is at 90^o, the tangent must be greater than the chord. Therefore the chord cannot be zero. If the chord is zero, then the tangent and the chord are equal: therefore the chord is not zero. To put it into a more proof-like form:

1) If the chord AB is zero, then the tangent AD is also zero.
2) zero = zero
3) If AB = AD, then the angle ABD must be less than 90^o.
4) The angle ABD cannot be less than 90^o.
QED: AB does not equal AD; AB does not equal 0.

In fact, this is precisely the reason that we can do calculations in Newton’s “ultimate interval”, or at the limit. If all the variables were either at zero or at equality, then we could not hope to calculate anything. Newton, very soon after proving these lemma, used a versine equation at the ultimate interval, and he could not have done this if his variables had gone to zero or equality. Likewise, the calculus, no matter how derived or used, could not work at the limit if all the variables or functions were at zero or equality at the limit.

Some will say that my claim that B never reaches A is like the paradoxes of Zeno. Am I claiming that Achilles never reaches the finish line? No, of course not. The diagram above is not equivalent to a simple diagram of motion. B is not moving toward A in the same way that Achilles approaches a finish line, and this has nothing to do with the curvature. It has to do with the implied time variable. If we diagram Achilles approaching a finish line, the time interval does not shrink as he nears the line. The time interval is constant. Plot Achilles’ motion on an x/t graph and you will see what I mean. All the little boxes on the t-axis are the same width. Or go out on the track field with Achilles and time him as he approaches the finish line. Your clock continues to go forward and tick at the same rate whether you see him 100 yards from the line or 1 inch from line.
      But given the diagram above and the postulate “let B go to A”, it is understood that what we are doing is shrinking both the time interval and the arc distance. We are analyzing a shrinking interval, not calculating motion in space. “Let B go to A” does not mean “analyze the motion of point B as it travels along a curve to point A.” It means, “let the arc length diminish.” As the arc length diminishes, the variable t is also understood to diminish. Therefore, what I am saying when I say that B cannot reach A is that Δt cannot equal zero. You cannot logically analyze the interval all the way to zero, since you are analyzing motion and motion is defined by a non-zero interval.
      The circle and the curve are both studies of motion. In this particular analysis, we are studying sub-intervals of motion. That subinterval, whether it is applied to space or time, cannot go to zero. Real space is non-zero space, and real time is non-zero time. We cannot study motion, velocity, force, action, or any other variable that is defined by x and t except by studying non-zero intervals. The ultimate interval is a non-zero interval, the infinitesimal is not zero, and the limit is not at zero. The limit for any calculable variable is always greater than zero. By calculable I mean a true variable. For instance, the angle ABD is not a true variable in the problem above. It is a given. We don’t calculate it, since it is axiomatically 90^o. It will be 90^o in all similar problems, with any circles we could be given seeking a velocity at the tangent. The vector AD, however, will vary with different sized circles, since the curvature of different circles is different. In this way, only the angle ABD can be understood to go all the way to a zero-like limit. The other variables do not. Since they yield different solutions for different similar problems (bigger or smaller circles) they cannot be assumed to be at a zero-like limit. If they had gone all the way to some limit, they could not vary. A function at a limit should be like a constant, since the limit should prevent any further variance. Therefore, if a variable or function continues to vary under a variety of similar circumstances, you can be sure that it is not at its own limit or at zero. It is only dependent on a variable that is.

If AB and AD have real values at the limit, then we should be able to calculate those values. If we can do this we will have put a number on the “infinitesimal.” In fact, we do this all the time. Every time we find a number for a derivative, we put a real value on the infinitesimal. When we find an “instantaneous” velocity at any point on the circle, we have given a value to the infinitesimal. Remember that the tangent at any point on the circle stands for the velocity at that point. According to the diagram above, and all diagrams like it, the tangent stands for the velocity. That line is understood to be a vector whose length is the numerical value of the tangential velocity. It is commonly drawn with some recognizable length to make the illustration readable, but if it is an instantaneous velocity, the real length of the vector must be very small. Very small but not zero, since we actually find a non-zero solution for the derivative. The derivative expresses the tangent, so if the derivative is non-zero, the tangent must also be non-zero.
      Some have said that since we can find sizeable numbers for the tangential velocity, that vector cannot be very small. If we find that the velocity at that point is 5 m/s, for example, then shouldn’t the velocity vector have a length of 5? No, since by the way the diagram is drawn and defined, we are letting a length stand for a velocity. We are letting x stand for v. The t variable is not part of the diagram. It is implicit. It is ignored. If we are letting B approach A, then we are letting t get smaller. A velocity of 5 only means that the distance is 5 times larger than the time. If the time is tiny, the distance must be also.

There is another way to analyze Newton's problem, and it may be the most interesting of all (for some). In the Principia, Newton's actual language in describing this problem (Lemma VI) is this: "if the points A and B approach one another. . ." Two things bear closer attention here. One, A cannot approach B without messing up the geometry. If we start moving the point A, we destroy our right triangle. What he means is what I have said above: Let B approach A. To be rigorous, we should let one point remain stationary and let the other point move. If we let both move, we create unnecessary problems. The other thing to notice is the word "approach". Newton is postulating motion. As confirmation of this, we need only look at his title for this section: "Of Natural Philosophy". Natural philosophy is not pure math, it is physics. Newton is describing a philosophy or study of nature, which we now call physics. Nature is not pure, it is physical. Therefore this lemma must be a part of what we now call applied mathematics. If this is so, then time must be involved. As I have asserted above, Newton is studying a diminishing interval in order to analyze curved motion. He uses this analysis immediately afterwards to apply to an orbit, for instance. So both motion and time are involved in Newton's analysis. For this reason alone, his angle BAD cannot vanish. That would be taking the problem to a zero time interval, and there is no such thing as a zero time interval in physics. You cannot study motion and then postulate a zero time interval, since motion is defined by a non-zero time interval. If you have a zero time interval, you have no motion, by definition. Simply by using the word "approach", Newton has ruled out a zero time interval. His interval can get smaller and smaller, to any extent he likes, but it cannot vanish. By definition, "approach" and "vanish" are mutually exclusive.

But it gets even more interesting. Using the limit concept alone, this problem cannot be solved at all. Meaning, if we let our angle at R equal θ, then BAD = θ/2 and ABD = π/2 + θ/2.



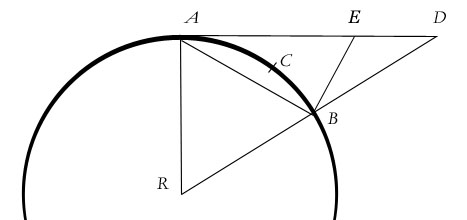
If we let θ go to zero, then BAD and ABD approach the limit in the same way. The limit concept does not support my analysis. No, it supports Newton's analysis, since historically it grew out of his analysis. The limit concept fails to explain why we find non-zero solutions at the limit for both the chord and the tangent, and it fails because its analysis is faulty just as I have shown Newton's analysis is faulty. The limit analysis treats the entire problem as an abstract or pure-math problem, whereas it is a physical problem. Motion and time are both involved here. What that means is that we must have a necessary time separation between A and B. Since we have motion, we cannot have a zero interval. If we do not have a zero interval, then we must have a time separation. Stated that way, we arrive at. . . yes, Relativity. If this is a physical problem, then A and B cannot exist the same time, operationally. An event at B cannot be fully equal to that same event as seen from A. If we think of the measurement of an angle as a physical event instead of an abstract geometric quantity, then angles in a diagram like this must be analyzed from a physical point of view.

Some will think I am overcomplicating this problem, or inventing esoteric solutions, but consider this fact: Newton's gravitational studies and proportionalities came out of this same book, the Principia, indeed this same section. Is it not strange that Einstein's Relativity corrections have been applied to gravity but not to the orbit? The diagram above is a preliminary study of the orbit, and underlies a=v²/r, and yet it has never benefitted from a Relativity analysis until now. We think that gravity causes the orbit, and yet we do a Relativity analysis of gravity but not of the orbit. Very strange.

The way that Relativity solves this problem once and for all is that it gives us a way of separating θ/2 at B and θ/2 at A. According to the limit analysis, both angles should diminish in the same way. But because they are spatially separated, they cannot act the same. According to Relativity, we must pick a point and measure everything from there. We must study the problem from A or B, but we cannot study the problem from both places simultaneously. Since we have given the motion to point B, we must let that be our point of measurement. In other words, in this problem, we exist at B. The event is at B. Let that event be π/2 + θ/2 going to the limit. θ goes to zero, so ABD goes to 90^o. Of course BAD is also going to zero, but there is a time lag. As seen or measured from B, information from A must be late, and vice versa. Therefore, as measured from B, the limit at B must be reached before the limit at A. Or, since I have shown that limits are never really reached anyway, especially when those limits are at zero, it would be more rigorous to say that θ/2 is smaller at B, as measured from B, than θ/2 at A. Given time separation, equal angles are not quite equal.

Of course, many people will not like this analysis. Some will find it fascinating and others will find it to be gibberish. Honestly I prefer the simpler explanation myself: we cannot propose a zero time interval, therefore the angles cannot vanish, therefore the lines cannot be equal. No matter how small we go, in order to talk of motion we must have a real time interval. As long as we have a real time interval, we have a triangle. As long as we have a triangle, we have a tangent that is longer than the chord. We "approach" the limit, we do not "reach" the limit. That said, I believe the Relativity analysis is also correct. Either analysis gets the right answer, using ideas that are physically correct and physically real. To be consistent, if we apply time separations to the gravitational field, we must also apply them to the orbit. Gravity cannot physically cause the orbit, Relavity applying to gravity but not to the orbit. Since Newton's whole section in question here is physical, we must either apply Relativity to all of it, or to none of it. Einstein updated Newton's analysis of gravity, and I have just done the same for the orbit.

Conclusion

My finding in this paper affects many things, both in pure mathematics and applied mathematics. I have proven, in a very direct fashion, that when applying the calculus to a curve, the variables or functions do not go to zero or to equality at the limit. This must have consequences both for General Relativity, which is tensor calculus applied to very small areas of curved space, and quantum electrodynamics, which applies the calculus in many ways, including quantum orbits and quantum coupling. QED has met with problems precisely when it tries to take the variables down to zero, requiring renormalization. My analysis implies that the variables do not physically go to zero, so that the assumption of infinite regression is no more than a conceptual error. The mathematical limit for calculable variables—whether in quantum physics or classical physics—is never zero. Only one in a set of variables goes to zero or to a zero-like limit (such as the angle 90^o). The other variables are non-zero at the limit. For QED, this means that when the Planck limit is reached, length and time limits are also reached. Neither time nor length variables may go to zero when used in momentum or energy equations of QED. In fact, beyond the logic I have used here, it is a contradiction to assume that values for energy would not have an infinite and continuous regression toward zero, but that values for length and time would.
      This is not to say that length and time must be quantized; it is only to say that in situations where energy is found empirically to be quantized, the other variables should also be expected to hit a limit above zero. Quantized equations must yield quantized variables. Space and time may well be continuous, but our findings–our measurements or calculations—cannot be. Meaning, we can imagine shrinking ourselves down and using tiny measuring rods to mark off sub-areas of quanta. But we cannot calculate subareas of quanta when one of our main variables—Energy—hits a limit above these subareas, and when all our data hits this same limit. The only way we could access these subareas with the variables we have is if we found a smaller quantum.

As I said, there has also been confusion on this point in the tensor calculus. In section 8 of Einstein’s paper on General Relativity, he gives volume to a set of coordinates that pick out a point or an event. He calls the volume of this point the “natural” volume, although he does not tell us what is “natural” about a point having volume. General Relativity starts [section 4] by postulating a point and time in space given by the coordinates dX₁, dX₂, dX₃, dX₄. This set of coordinates picks out an event, but it is still understood to be a point at an instant. This is clear since directly afterwards another set of functions is given of the form dx₁, dx₂, dx₃, dx₄. These, we are told, are the “definite differentials” between “two infinitely proximate point-events.” The volume of these differentials is given in equation 18 as
dτ = ∫dx₁dx₂dx₃dx₄
      But we are also given the “ natural” volume dτ₀, which is the "volume dX₁, dX₂, dX₃, dX₄". This natural volume gives us the equation 18a:
dτ₀ = √-gdτ
      Then Einstein says, “If √-g were to vanish at a point of the four-dimensional continuum, it would mean that at this point an infinitely small ‘natural’ volume would correspond to a finite volume in the co-ordinates. Let us assume this is never the case. Then g cannot change sign. . . . It always has a finite value.”
      According to my disproof above, all of this must be a misuse of the calculus, a misuse that is in no way made useful by importing tensors into the problem. In no kind of calculus can a set of functions that pick out an point-event be given a volume—natural, unnatural, or otherwise. If dX₁, dX₂, dX₃, dX₄ is a point-event in space, then it can have no volume, and equation 18a and everything that surrounds it is a ghost.
      In the final analysis this is simply due to the definition of “event”. An event must be defined by some motion. If there is no motion, there is no event. All motion requires an interval. Even a non-event like a quantum sitting perfectly still implies motion in the four-vector field, since time will be passing. The non-event will have a time interval. Every possible event and non-event, in motion and at rest, requires an interval. Being at rest requires a time interval and motion requires both time and distance intervals. Therefore the event is completely determined by intervals. Not coordinates, intervals. The point and instant are not events. They are only event boundaries, boundaries that are impossible to draw with absolute precision. The instant and point are the beginning and end of an interval, but they are abstractions and estimates, not physical entities or precise spatial coordinates.
      Some will answer that I have just made an apology for Einstein, saving him from my own critique. After all, he gives a theoretical interval to the point. The function dX is in the form of a differential itself, which would give it a possible extension. He may call it a point, but he dresses it as a differential. True, but he does not allow it to act like a differential, as I just showed. He disallows it from corresponding to (part of) a finite volume, since this would ruin his math. He does not allow √-g to vanish, which keeps the “natural” volume from invading curved space.
      Newer versions of this same Riemann space have not solved this confusion, which is one of the main reasons why General Relativity still resists being incorporated into QED. Contemporary physics still believes in the point-event, the point as a physical entity (see the singularity) and the reality of the instant. All of these false notions go back to a misunderstanding of the calculus. Cauchy’s "more rigorous" foundation of the calculus, using the limit, the function, and the derivative, should have cleared up this confusion, but it only buried it. The problem was assumed solved since it was put more thoroughly out of sight. But it was not solved. The calculus is routinely misused in fundamental ways to this day, even (I might say especially) in the highest fields and by the biggest names.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.