return to homepage
return to updates

Rainbows, Prisms, and non-edge Diffraction:
A Rehabilitation of Goethe

by Miles Mathis

Abstract: I will explain diffraction mechanically, using the unified field, a historical first. I will also explain prism refraction using the unified field, something that has also never been done. Finally, I will show mechanically how bands of dark and light can cause diffraction without any material edges. This extension of historical theory will prove that Goethe and Newton were both wrong and both right. Goethe was right about green and non-edge diffraction, while Newton was right in giving his corpuscles spin to explain their motion through the prism. In this way I will continue to turn history on its head: not only will Goethe, who is thought to be wrong about most things, be shown to be right about many of them; but Newton will be shown to be right about one of the (few) things he is still considered to be wrong about.

I will begin by quoting Goethe's criticism of Newton. I do this despite the fact that I am here to correct Newton, not to bury him. I have the highest regard for Newton and am quite sure his optics was a necessary step in history. That said, I feel that Newton is just as fair a target as Goethe. Goethe has taken more than his share of hits in past 200 years, and it is past time Newton was subjected to another thorough analysis. No one should be protecting Newton from fire, either mine or Goethe's. Beyond that, Goethe's criticism, although dismissed by modern physicists, is quite simply glorious. To see that, you do not need to be a hater of Newton, only a lover of polemics. Couched in the language of Goethe, this criticism would be glorious even if it were false; but it is not. Unfortunately, the modern translations ditch a large part of Goethe's criticism, leaving us only with the gems in the preface to part 1, such as this one:

Thus there is no question here respecting a tedious siege or a doubtful war; no, we find this eighth wonder of the world already nodding to its fall as a deserted piece of antiquity, and begin at once without further cememony to dismantle it from roof and gable downwards, that the sun may shine at last into the old nest of rats and owls, and exhibit to the eye of the wondering traveler that labyrinthine, incongruous style of building with its scanty makeshift contrivances, the result of accident and emergency, its intentional artifice and clumsy repairs. Such an inspection will, however, will only be possible when wall after wall, arch after arch is demolished, the rubbish at once being cleared away as well as it can be.

As I said, glorious to the last word, and the more glorious because true. And the even more glorious in that it can be led forward in history and made to apply to all of physics since then, in all sub-fields. That one paragraph mirrors my entire critique of the 20th century, though it was written in 1810. Goethe's polemics had to be jettisoned and reviled, since it could not be answered. Who was available then to launch a counter-attack? Who is available now? You might as well attack a threshing machine with a pocket knife. No, the only way to answer is to censor and ignore and fail to translate. Physics was still following this method in the 1960's, when it “debated” Velikovsky, but conveniently forget to invite him to the debate. It is still following this method by limiting the current debate to a few minor variations of the standard model, and the debaters to a handful of insiders who have been pre-chosen by years of rule-following.

Although my explanations of diffraction and refraction go beyond both Goethe and Newton, and basically falsify both, my explanations also confirm large parts of each man's theories. Depending on your perspective, this paper can either be seen as a synthesis or an analysis. In my personal opinion, it is both synthesis and overcoming. I pull together the best parts of both theories and then, using the charge field, go well beyond them. I see it as synthesis because I admire both men. I think they were both geniuses of the first order. If I lean to Goethe here in my title, it is mainly to balance the scales. Newton has gotten his full due on this problem, and then some. Goethe has not. Goethe was immediately leapt upon as an outsider, and he still is. Then, as now, physics was protective of its game. For obvious reasons, I find that repugnant. It is all-too-human, and therefore understandable, but it is non-scientific. Besides, Newton has no lack of defenders; but Goethe is in need of my tongue. It may not be as pretty as his was, but it is often nearly as sharp, and is always just as ready.

But to move on. I only wished to point out this very interesting side-street; I do not wish to walk it in this paper. I intend to talk about physics, not about politics. As a first physical and optical topic, we will talk about the color green. I remind you that Goethe had very little respect for green. He thought it was close to grey, and put it at the bottom of his six color rankings. Yes, he ranked his colors, and mixed a small dose of mysticism into his theories. This is how people like Steiner were able to run with these theories, expanding on the mysticism and mostly ignoring the science of it. But, from what I have read, it appears Goethe's optics were ripe for this sort of expansion, since his science is already tinged with this non-science. He might have left off the moral chapters of his book, and suited me just as well.

However, I am not here to evaluate all that, either. Everybody's science was tinged with non-science in the 18th century, and it still is. Newton's science was also heavy with non-science, but his proponents have conveniently hidden all his most embarrassing statements. I simply want to look more closely at green, in light of my recent discoveries about the photon. Reading about Goethe's theory of color allowed me to do that, and his illustrations and experiments allowed me to discover some of the things I will relate to you here.

As an artist, this problem has a natural fascination for me. I have always painted as an intuitionist, never getting too involved in color theory, but any problem that combines art and physics will have my full attention. It turns out that some colors that artists use aren't found on the normal “prismatic” wavelength spectrum. That spectrum runs violet, indigo, blue, green, yellow, orange, red. Magenta is not on that list, as you see, and you can't create it by mixing any of those adjacent colors. You can create it from mixing violet and red, but those colors are on opposite ends of the visible spectrum. It turns out that is a big clue here. The very fact that we have non-prismatic colors is very strange in itself, and modern color theory really tries to sweep it under the rug. Just do a websearch on “non-prismatic color” and you will see what I mean.

According to current theory, magenta is a mixed tone, created in the eye. No photons are magenta. To see magenta, you need a field of mixed red and violet photons. Both impinge on your eye, and your eye superimposes them, like transparencies. Well, kind of. According to About.com**

All of the colors of light have complementary colors that exist in the visible spectrum, except for green's complement, magenta. Most of the time your brain averages the wavelengths of light you see in order to come up with a color. For example, if you mix red light and green light, you'll see yellow light. However, if you mix violet light and red light, you see magenta rather than the average wavelength, which would be green. Your brain has come up with a way to bring the ends of the visible spectrum together in a way that makes sense. Pretty cool, don't you think?

No, I don't think. What I do think is that is a terrible answer. How can anyone think that is worth putting up on the web, or putting into print? It doesn't answer the question asked, and begs about ten different questions. According to this PhD, your brain creates a color from whole cloth, simply to fill a gap, and it just happens to be one of the primaries of CMY. Talk about a circular argument!

Problem is, current theory doesn't think this about green, although it is also true of green. Goethe appears to have known this about green, which is why I am giving him credit here. He knew that no pure light is green. Green light is a mixture of yellow and cyan light, and it is created in the eye. Technically, you can say that green exists outside the eye, as long as you are careful to define it as a field of both photons. But, more rigorously, the color green isn't really created until your eye superimposes both responses. An eye that couldn't read two colors at once in this way, and superimpose them, couldn't see green. This is why people who are colorblind can't see green. All three major types of colorblindness are green-blind, and that is another big clue. If green is a pure wavelength or a primary, then why would lack of red receptors cause green blindness? According to current theory, a lack of red receptors should cause yellow blindness, since yellow is red plus green. Most colorblind people should see green but not red or yellow. Instead, they see yellow but not red or green.



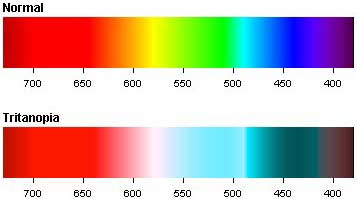
To be rigorous from the beginning, what I will show here, among many other things, is that green is not a wavelength of the photon. Since the term “light” is normally used to refer to averaged light, or a field sample, green certainly exists as a wavelength of light, just as do blue or red. But in this paper I am not concerned so much with light or with color: I am concerned with the wavelength of the photon itself. Yes, I have shown in a series of other papers that each individual photon has a wavelength. In this paper, I will show why the photon cannot be green. I will show that it cannot be blue, either. It cannot be orange. It cannot be indigo. It cannot be magenta.

You will say that is because color is a physiological phenomenon, so that the photon cannot truly be any color. But that is not my point here. I have never been too interested in that kind of speech, and I still am not. No, I will show that the photon cannot be green or blue or orange, but I will show that the photon CAN be emitted at wavelengths that corresponds to violet and dark red, and that it CAN be shifted by the charge field to a wavelength that corresponds to yellow or cyan. In this way I will show that we have four pure colors or primaries existing in the visible spectrum (or very near it), and that two of those are fundamental emitted primaries.

This is the first way that I can show that Goethe was right and Goethe was wrong. Goethe was right in that he believed there were four primaries, of this sort. He did not speak of photons, but otherwise his analysis was very similar to mine. He had the same colors, and called them primaries for the same reason. His only problem was getting them reversed. He thought yellow and cyan were the originals, and red and violet were the shifted colors. The only reason I knew he couldn't be right, as I show below, is that I knew the two original colors or wavelengths had to be further apart on the spectrum than yellow and cyan. Yellow and cyan are too close to each other, simply as a matter of wavelength, and cannot be created by freshly emitted photons.



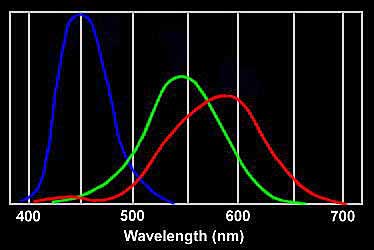
If you look at this illustration, you will see that although they tell you light receptors in the eye are for red, green, and blue, they spin this information to match modern colorimetry. Of the three types of cones in the eyes, all receive over a broad band. The green receptors also receive yellow, blue and orange, as you see, and the red receptors also receive yellow and green. Both the red cones and the green cones peak very near yellow; and if we average the two peaks, we are right above yellow. Look where the green lines and the red lines cross. Amazingly, the red and green lines also cross at cyan. They never tell you that: you have to take it from their own graphs yourself. But it is quite important, and it ties into my comments on yellow and cyan below. [Also, note how the red line has a strange second peak in the violet wavelength, almost as if it is trying to detect magenta.] Beyond that, they have colored the red line red, despite the fact that it doesn't even peak in red. As you can see, it peaks at 580, which is still yellow. Why color that line red then? Also, green normally peaks at 510, but here we see the peak at 545. That's a very yellow-green, but they don't tell you that. Finally, they color the blue line blue despite the fact that blue actually peaks at 475. According to this illustration, the cone peaks at 450, which is indigo, not blue. They are pushing the interpretation toward RGB, despite the fact the cone peaks don't show RGB. They show indigo, yellow-green, and yellow, which would be I/G-Y/Y.

The standard answer to this crossing of the green and red lines above yellow is that the eye creates yellow by stacking red and green, or stacking red and green responses. But that explanation is pushed. The eye cannot create colors by stacking that way, since the retina is not white. You can only create yellow by the additive method when your background is both white and reflective, as with the projected light in the illustration below. So red and “green” cones must be firing together with yellow for another reason. I suggest they are firing to determine how orange or green the yellow is, not to “create” it.



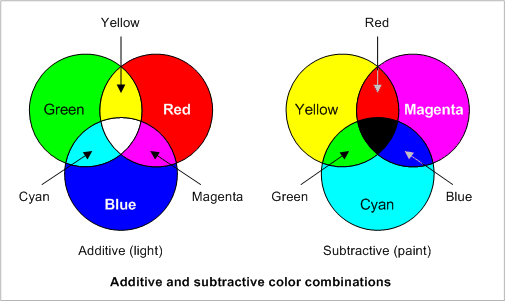
An expert on light mixing will say that Helmholtz proved that cyan light and yellow light do not mix to create green light, but that is false. Helmholtz did not disprove Goethe's mixing by rerunning Goethe's slit experiment and showing it was false, he tried to disprove it by running a different experiment with colored lights. Helmholtz got grey light, and concluded Goethe was wrong. The same sort of argument is made today by combining yellow light and blue light to get white light. But, although this combining is true and is easy to show, it isn't the same sort of combining Goethe was doing with his slit, so it doesn't disprove Goethe's experiment or illustration. All it does is prove that in some experiments, blue light and yellow light creates white light, while in others it creates green light. We are then left to explain why the experiments get radically different results. I will do that below.

Many people in history have thought that green light was a mixture, and some people still think this, thanks to Goethe and Steiner and Brewster, but until now no one was able to prove it one way or another. These people who think green is a mixture have always been dismissed contemptuously as “artists” or Aristotelians. Who now wants to be called an Aristotelian? Not even artists want to be called Aristotelians. But my paper called “How do Photons Travel?” has allowed me to do the pretty simple math and mechanics, showing that the green wavelength is impossible to create with photons themselves, due to quantum and spin considerations. Interestingly, Newton never claimed that green was a primary. Newton showed the prismatic split, but was never much interested in colorimetry. As I will show below, the preference for green over yellow didn't happen until Young chose green over yellow (on his second try) in the beginning of the 19th century, and this choice was put in stone by Maxwell in the middle of the same century.

Of course, we can find proof against green as a primary straight from the figure above. Remember that About.com, a voice of the mainstream, has already admitted that magenta is a mix. That means it can't be a primary. Magenta is composed of red and violet, which gives us red, violet, yellow, and cyan as the four primaries of CMY. Four primaries, which proves my theory without any more argument. But if we look at the two charts together, we see that green is the analog (or opposite) of magenta. Green holds the place in RGB that magenta holds in CMY. Therefore, if magenta is not a primary, green cannot be a primary. They call green a color-mixing primary for the same reason they call magenta a color-mixing primary: it can be made to hold a place in these manufactured trios. But neither magenta nor green is a real primary, since they can both be split. RGB is a misdirection, since it relies on reflection from a white wall, where all the colors already exist. When talking of colorimetry or real primaries, we should always look at the so-called subtractive method, or CMY. There we see that yellow and cyan cannot be split, making them true primaries. There is no subtractive method of making yellow or cyan out of other colors. Only magenta is capable of further splitting. This gives us four primaries, none of which is green. Green, like magenta, is a mix.

Before I show the proof against green from photon mechanics, let me try one last time to deflect criticism before it gets loud. I am not claiming that modern colorimetry based on Maxwell is completely wrong or that light with an average wavelength of 500nm does not exist or that the retina does not process light of that wavelength. Both our eyes and our machines see or measure the wavelength of a set of photons, not the wavelengths of individual photons. This measurement is always an average (About.com was partially correct). So while green certainly exists as an average, and it exists in colorimetry, and receptors for it exist in the eye, it does not exist as expressed by individual photons. That is my only claim here. That claim may be accepted with more or less grace when I add to that claim that this is also true of blue light, most red light, and most violet light. Almost all prismatic light is a mix, and only narrow bands of the spectrum can be called pure. I will show that four bands can be called pure, and only two of those can be called emitted. Yes, only two wavelengths are actually emitted. The other two pure bands are caused by refraction or diffraction by the charge field, and the rest of the prismatic spectrum is caused by mixing.

In my photon papers, I have shown that the wavelength we see is actually a local wavelength of the individual photon that has been stretched out by its linear motion. The local wavelength is caused by spin, so the spinning photon will have a very fast local frequency. This frequency is about 10¹³ cycles per second (for an infrared photon). The local wavelength is just the radius of spin, which is about 10^-24m. The orbital velocity of this spin is 1/c, and the linear velocity of the photon is of course c. Therefore, the local wavelength is stretched out or increased by c². That is where the c² comes from in Einstein's famous equation.

Using this simple analysis, we see that the quantum or integer value here is the radius of the spin, which is also the local wavelength. In other words, that is our baseline, our number 1. To get a larger wavelength, we have to increase the radius of spin. But we can't do that unless we double the quantum spin number: we have to jump up to the number 2. That is how the wavelength is quantized. I showed the mechanical reason for this in my paper on superposition. To increase the size of a spin, and therefore the local wavelength, you can't just expand the spin radius like a balloon. You have to stack a second spin on top of your first spin, and this outer spin then creates your new larger spin radius.

To stack a spin on top of an existing spin, you have to obey gyroscopic rules, which means you have to go beyond the influence of the inner or existing spin. In other words, your second spin has to be an end-over-end spin, beyond the reach of the first spin. If our first spin was an axial spin, for instance, our second spin will have to be an x-spin. You can't have two axial spins, since the second would interfere with the first.

Given that, if the radius of your first spin was 1, the radius or your second spin must be 2. If you need a third spin, it will be of value 4, and so on. You can have a spin value of 1, 2, 4, 8, etc, but you cannot have a spin value of 1.5, 3, 5, 7, or any other value that is not a multiple of 2.

If we apply that to the visible wavelength of light, we see that many wavelengths will be impossible. To create a visible wavelength, you take a local wavelength and multiply by c². So, if we take our spin quantum to be 10^-24m, then our detectable wavelengths will be 9 x 10^-8, 1.8 x 10^-7, 3.6 x 10^-7, 7.2 x 10^-7, etc. If the spectrum we can see is only about 3 x 10^-7m wide, then we cannot have 7 different photons creating it. In fact, we cannot have even four. We can have only two (and one of those is just off the spectrum).

Yes, from this analysis, it would appear we must create all known colors from only red and violet photons. That will shock even the followers of Goethe and Steiner, since according to them the two primary colors should be blue and yellow, the color of sun and sky. And, admittedly, it shocked me, too. I came into this paper expecting to have four photons in the spectrum: red, yellow, blue, and violet. How can we create all the colors from just red and violet? Green, orange, and indigo are easily lost, since they are clearly mixes, but how can we use red and violet to get yellow or blue?

Before the computer age, I would not have believed it, but after working with photoshop, I now think I understand it. Remind yourself that the two color mixing charts are now RGB and CMY. Red, green, blue and cyan, magenta, yellow. To a painter, neither of those charts makes any sense. In painting, the primaries are red, blue and yellow; but paint mixing is not like photon mixing. In RGB, you stack green and red to get yellow. If you stack green and red in paint mixing, you get grey, because the two are opposites. You can never achieve yellow from a mix of other colors.



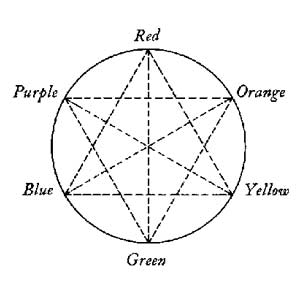
Goethe's six sided star or circle of hues matches RGB and CMY much better than Newton's seven prismatics. The blue of RGB is a purplish blue, for instance, and by red it is known that Goethe meant magenta. His blue is a cyan blue, so his color star is basically equivalent to the current designer's wheel. Using colored light, we see that the outer large circles are RGB, with the inner colors being CMY, with cyan opposite red and so on. In this limited sense, we may say that Goethe knew more about color than Newton. Not about light, but about color. This is not surprising, since Goethe had studied painting. He knew more about color going in than Newton ever did.

This entire problem doesn't begin to make sense until we differentiate between light and color, between photons and colors. Neither Newton nor Goethe were rigorous in their separation of light and color, and the rigor is still lacking in modern optics. We get a lot of talk about physics versus physiology, but the solution is not in any separation or distinction of that sort. The solution is in looking at photons, and no one has been in a position to do that until now. Wave theory pushed Newton's corpuscles to the side until the early 20th century, when the photo-electric effect and the Compton effect revived them in a big way. But even then the photon was buried under the ridiculous wave/particle duality and the Copenhagen interpretation, which forbade anyone from looking closely at the photon. In the 20th century, and up to the present time, the photon has been a point particle, with no mass and no radius. It couldn't be given a real spin under those circumstances, and so no one has been able to apply the math and mechanics I am now applying to the problem of color and wavelength. Physicists were prevented from doing what I am doing both by the Copenhagen interpretation and by the gauge math of QED. Although my giving the photon spins is great for solving superposition and entanglement problems, it is a terrible threat to the entrenched maths of the standard model. Giving the photon mass and spin endangers most of the ad hoc mathematical manipulations of the past half-century, and all the Nobel Prizes perching on this math, so you can expect the mainstream to resist my simple solutions to their last breaths.

Again, we have four basic colors to work with (the others being mixtures), but those four colors are created by only two photon wavelengths. To see this more clearly, we just have to look at the common split using a small slit, as both Newton and Goethe did. Light comes into a darkened room through this slit and is split like this:



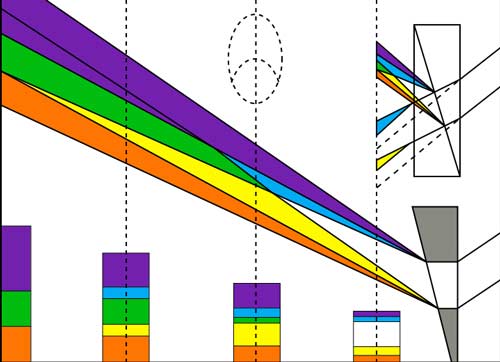
This is Goethe's illustration, but even Newton would not necessarily disagree with it. Newton simply used a prism to make a further split between violet and blue and between red and yellow, achieving orange and indigo. Remember that Newton's and Goethe's experiments were roughly the same: both used a hole or slit to let light into a darkened room (si per foramen exiguum: if through a small hole). But Goethe showed that Newton's prismatic spread, including green, could only be achieved at a certain distance from the hole in the wall. That is what we see in the illustration. If we move further from the slit, we get different spectra. At a shorter distance, we don't get green at all.



We see from the illustration precisely why Goethe considered green to be a mix. But we get somewhat less theory from him on the other four colors. Goethe says that these colors are caused by the edges between darkness and light, but he never takes the mechanics much beyond that. Why do the edges create two colors instead of one, and why does the lower edge create one pair and the upper edge create the other?

The answer is fairly simple, although I have never seen it from Goethe, Newton, or anyone else. Newton never addressed the question of dark and light bands creating a color split by themselves, without physical edges to diffract or refract; and Goethe, although he did precisely this, always kept to the effects and never addressed the causes. Goethe never talked photons, or tried to find any other mechanism for the effect. Notice that in Goethe's illustration, the red pair is on the short side of the gap. In fact, the gap is like an upside down prism. The blue light has a longer edge to pass. We find the same thing from a prism, since if the point is on top, the red is also on top. The red always chooses the short side. Newton tells us that violet is bent more by the prism, and that this explains the apparent “choice”, but he never tells us why the violet light is bent more. We still aren't given a sensible answer to this day. Newton was right: the violet appears to be bent more. But I can tell you both how and why.

Newton initially tried to explain it with spin, but he was shouted down by Hooke and Huygens, and his spin model is still being repressed as an embarrassment. Without spin, the modern explanations are not really mechanical explanations at all. They are just descriptions. A substance is given a refractive index, and this index causes the bend. But of course that is heuristic, not mechanical. It explains nothing. It is to say that violet is bent more because the substance bends it more. The refractive index causes the bend and the bend determines the refractive index: mechanics=zero.

According to Goethe, the light had already been split by the hole in the wall, and this would explain it because red was already on top to begin with. Goethe didn't try to explain refraction by bends, but those who came after thought that maybe the greater bend of blue could then be explained because it is in the prism longer. That wasn't Goethe's answer, but it has been suggested by some. That answer isn't right, either, but we will leave that question open for now and go back to the wall. We will try to explain diffraction before we hit refraction. So why does the red light choose the short side at the wall? If the length of the gap causes the split, the longer side would be expected to change the light more, in whatever way it is changing it; but that still doesn't explain why we get red on the short side from the very beginning.

My answer is that the photons are pushed by the charge field, and red photons get pushed more because they have less energy. In Goethe's diagram, the photons are pushed down in the gap because the wall is thicker on top. The mass up there is recycling more charge, so the photons get pushed down. The red ones get pushed more, so they are below the others. In the prism, the distribution of mass reverses: more mass is below in the prism, so the charge field is moving up. So red moves up more than the other colors. We will study the prism in more detail below.

As I have already discussed in my paper on the two-slit experiment, in coming through the slit, the light must interact with the charge field emitted by the material in the wall. The charge field is photonic itself, and the field interacts with the light in a strictly mechanical way, via real collisions. This charge field cannot slow the linear velocity of the light appreciably (unless the light is going through the material itself), but it can certainly affect the spin velocity. In doing this, we could even say it has a magnetic effect on the light, since any spin effect on a photon can be defined as magnetic.

As the charge field emitted by the wall affects the spin velocity, it also affects the color. I have recently shown that the idea of wavelengths is skewed in current theory, so here I will talk of energy or color instead of wavelength. So what the small hole does is force the light very near the material in the wall. To get through the hole, the light has to pass very near the material, and therefore it passes through a fairly dense charge field. It is somewhat like bringing a magnet very near a refrigerator. At most distances, the refrigerator has no effect on the magnet, or vice versa. But at small distances, the effect increases dramatically. Same with light forced to go near matter. It encounters the charge field of matter much more strongly than usual, since the charge field emitted by the material has had no space to dissipate. Our light is being forced through a small charge field in the gap.

As you see, the splitting of red and violet into yellow and blue is also explained in the same way. The charge field in the gap simply acts to sort the light by energy, with the lowest energy traveling lowest and the highest energy traveling highest. The gap works exactly like an upside-down prism, and we now see that diffraction and refraction are basically the same thing. They are a sorting of light by a charge field.

This can be proved by looking at the second experiment Goethe did. Instead of running light through a slit, he ran it around a small object, causing diffraction at the outer edges of the object. The dark gap in the illustration represents the width of the object. As you can see, we get a very strange prismatic band, one that is not even Newton's band upside down. Red and violet are in the middle and yellow and blue are on the outside. Magenta is created in the middle instead of green.



Another equally large problem is that red is bent more than violet here. Refrangibility is a fancy word for this bending of light, and Newton proposed that the bend of each color was a constant. This "truth" is still the centerpiece of modern optics, and it used to explain rainbows, why the sky is blue, and most other phenomena. Unfortunately, modern physicists have no explanation for refraction around an object like this, or of refraction of a dark band passing through a prism, as shown in this GIF.

They do not deny that this happens in experiment, but they just ignore it whenever they attack Goethe or cheer for Newton. They say that Goethe ignored evidence, then they go on to ignore Goethe's evidence without comment. Bruce MacEvoy at Handsign¹ is among the worst in this regard, since he even prints Goethe's figure, while ignoring it.

One important mathematician who was not able to ignore this second illustration of Goethe's is Mitchell Feigenbaum, one of the fathers of chaos theory. We always hear that only artists fall for Goethe, but apparently that isn't so. My readers know that I don't have much use for non-linear math or chaos theory, but I take my allies where I find them. I was not able to find any indication whether Feigenbaum has upheld this defense of Goethe against what I know are ferocious odds, but I assume he has not backed down; otherwise he would have instructed Wikipedia to publish a disclaimer or update.

This experiment is always highlighted by proponents of Goethe, and it is indeed very important; but never before has anyone pointed out what I am about to point out to you. Notice that it proves my previous assertion concerning the role of charge here, since at both the top and bottom, the less energetic photon has gone above the more energetic one. In both cases, red is above yellow and blue is above violet. Light is not being at all careful to maintain its prismatic wavelength sequence, is it? It is not being at all careful to maintain its refrangibility. It is only being careful to maintain its relationship to the charge field. And although this animation doesn't show it properly, in the second case red/yellow are trying to go back above blue/violet. This is because the charge field of the Earth still exists beyond the far side of the prism, and the photons are trying to resort themselves relative to that field.

But back to the regular prism. The charge field will be emitted perpendicular to the face of the prism, so that if we have a 45^o prism, the charge field will be emitted 45^o up, and at a 45^o angle to the incoming light (if the light is flat). So, basically, the incoming light has encountered 45^o cross traffic at the boundary. But inside the boundary, the charge field is no longer at a 45^o angle. At the center of the prism, the charge field would be expected to be flatter, relative to the light, due simply to shape considerations. There is more emission below than above, because there is more matter below, so there must be more charge up at the boundary than in the middle of the prism. You may have to draw some vectors to see this, but it will become apparent pretty fast, I think.

Given that, there must be a charge force up on the light the whole way through the prism. It is bigger at the boundaries, but even at the center, the resultant force from the charge field is up. To prove that, imagine the incoming light hits the prism halfway up. Then let the light move through on a flat trajectory. It will hit the middle of the prism well above the center of mass of the prism, you see. If you are above the center of mass during your entire trip through the prism, then the charge force will be up the whole way.



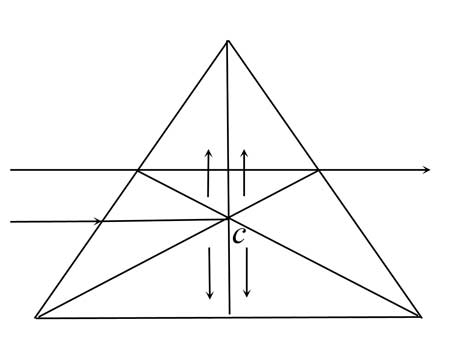
To make the light pass through the center of mass of the prism you would have to let the light hit the face of the prism about 2/3rd's of the way down. In fact, this is why the prism won't split light that impinges on it too low. If you let the narrow beam hit below the 1/3rd level, in the fat part of the prism, the charge field won't work as I am explaining. This is another one of the things they always hide from you, since they can't explain it.

This also explains the slowing of light in a material. If the emission at the surface of the prism is 45^o, then only half the energy of that emission is up. Half of it is against the incoming beam. The light is not just encountering cross traffic pushing it up, it is encountering head-on traffic, slowing it. This means that light is slowed only in the first half of its trip through the prism. After it passes the center, it is re-accelerated back to its initial velocity, which is why it comes out of the prism at speed. Light passing through a prism, or any other transparent material, is not slowed all the way through, then accelerated instantly to its original speed at the far surface. That has never been logical. No, its speed is affected by the charge field, and the charge field sums out from the center of any object, getting greater near the surface. Newton thought that all effects happened at surfaces, but that is false. As I showed in my third paper on Feynman [see last part], surfaces are important, but only in that they limit the math and the effect. Mechanically, the surface is not so important. It is not the surface that causing the refraction, it is the charge field.

Now, the charge field of the prism is in the charge field of the Earth, and the charge field of the Earth was already going up, but the incoming beam of light was balanced relative to gravity and E/M before it hit the prism. That is why it hit the prism. That is how we aimed it. We created the balance. But when the light beam gets to the prism, the charge field of the prism is added to the charge field of the Earth, throwing off this balance. Since the prism has more mass low and less mass high, its internal charge field moves mainly up, especially in the top half of the prism. This is why the beam of light is always aimed at the top half of the prism.

Anyway, this explains the varying "bends" because the red light is driven up more than the violet light. So far I have simplified the mechanics by having charge lift red more, and while that is the result, the actual photon-photon interaction is somewhat more complex. It is a spin interaction, not a linear interaction. What this means is that all the different color photons are gaining energy in spin transference from charge, but the red ones are gaining the most. They gain the most energy because they are closest in size to the infrared photons that make up charge. See my more recent papers for more on this.



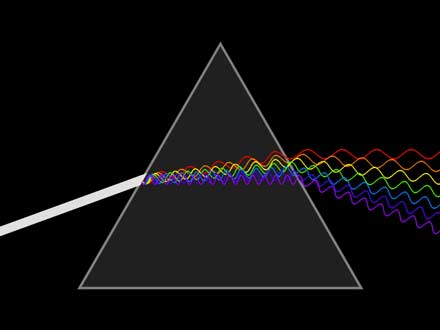
Just look at this illustration from Wiki, which confirms my analysis. It is not violet which falls, it is red which rises. This is of extreme importance, but no one has ever bothered to notice it. Many or most illustrations ignore or falsify this truth by letting violet fall. But violet never falls in a prism where the point is up. No, violet actually rises a tiny bit, and red rises more, due to bombardment from the charge field.

Before I move on, let me point out that the prism, as we are studying it here, is just a two-dimensional pyramid, pushed along the y-axis. In this way, this paper ties into my paper studying the charge field of the pyramid. Prisms, like pyramids, act to accelerate the charge field of the Earth up, by adding their own charge field to it.

I will pause to answer a question from my very astute critic. He or she will say, “If refraction is caused by this mechanical bombardment by the charge field, why doesn't red get slowed more than violet. If red responds more to charge, it should be slowed more, no?” No. We know that different colors and energies are not slowed more or less. NASA proved this only last year, as I showed in a recent paper about Hulu videos. Not only does the prism not slow different colors differently, millions of light years of space cannot slow them differently either. The action of the charge field on photons is mechanical, but the mechanics of it has to be studied closely. As I have shown in other papers, and as I show again below, photons do not slow eachother as a matter of linear velocity. They can deflect one another, and change eachother's energies, and cancel spins, but they cannot slow one another. This is because all photons that we can see or detect have spin. The spin is like an outer energy shell, and in any collision, it is this shell that is preferentially affected. As with baryons or leptons or any other quanta, photons have to have their spins stripped first, before anything can happen to the particles themselves. The spins act as protective shells. For this reason, individual photons are never slowed, even by dense material. What is slowed is the collection of photons, and they are slowed by deflection. This means that each individual photon is made to take a longer path to get through the material. A longer path implies an apparent slowing. Even Feynman understood this, since this is what his averaging or summing is about. Light cannot be slowed for any reason without breaking several good rules that I have no desire to break. It cannot even be slowed by going through material. This simple explanation allows us to keep the data we have that shows slowing, while giving the slowing to the path rather than to a lower velocity.

Now let us look at the light coming out of the prism. We have been talking about red and violet, but when the beam comes out of the prism, it is split further. We start to see yellow and green and so on. Why? Newton and Goethe couldn't tell you why, they could just point to the fact. Newton, deprived of his spinning corpuscles, can explain it only by ad hoc boundary conditions, and he got even these wrong. He thought that a refraction toward the normal was an increase in speed, when the reverse is true. Huygens used this major mistake to attack the corpuscle theory, but the mistake had nothing to do with corpuscles. It was a mistake in fundamental field mechanics, and could have been made with waves just as easily as with corpuscles. Huygens only avoided the error by theorizing nothing at this juncture.

Goethe, although disagreeing with Newton on the bend at the boundary, did not offer a better explanation. He did not replace Newton's description with a better description, he just replaced it with a different description. Neither man provided us with the fundamental mechanics.

Same for modern theory. Lacking a charge field, they can explain none of this. But with the charge field, it becomes pretty simple to explain. The red no longer gets the lift it was getting from the charge field in the prism, so it wants to fall back to its initial position. So it begins to do so. This is what causes the bending at that surface. However, it isn't that surface that causes the split into yellow. As with the gap we studied above, the split already occurred in the prism. We simply see the split after the light leaves the prism, because the air in the room diverts some of the light to us.



As another interesting example, study this illustration*. I assume it is an illustration rather than a photograph, but if we assume it is done correctly we must notice something odd. The second prism (on top) appears to have switched the red from bottom to top. The red has reversed its relative position. The two prisms are used in the first instance to increase the split, but notice that more than an increase is happening. The second prism is not only spreading the split, it is reversing it! Red exits above, even when it enters the prism on the down side.

If you don't see what I mean, turn the illustration on its side, like this:



Now you can see that the red is on the bottom going in and on the top going out. This is realy extraordinary, and it refutes current theory while confirming mine.

Let me summarize what we have found so far. We have seen that visible light is emitted at only two wavelengths. All visible light is originally red or violet. It can then become yellow or cyan when its spin speed is slowed by diffraction or refraction—by close contact with a charge field. Magenta and green are then created by a mixing of these four colors. This means that yellow and cyan wavelengths do exist, but they have to be created by charge interaction, since they can't be emitted.

By this analysis, red and violet photons are pure or fundamental photons, being emitted that way by matter. Yellow and cyan photons are secondary photons, since they are created by charge fields. Green and magenta photons do not exist, so these colors can be called optical tertiaries. Green is yellow plus cyan.

But this still doesn't explain why yellow and cyan are so special: why they have narrow bands to themselves; why they make up two-thirds of the CMY trio; and why I should treat them as semi-primaries. Can't the charge field push red short of yellow, or past it? Can't the charge field push violet short of cyan or past it? It would appear that in most cases, the answer is no. If a narrow slit in a wall can push red to yellow, then it must take a small charge field to maximize the push. And I cannot let that push go past yellow into green without jeopardizing my title and my whole argument here. So why does the charge field push red to yellow, and no further?

Well, unless light is meeting charge head-on, charge tends to increase the energy of light. That is what is happening here. Huygens was wrong regarding diffraction, because he ignored the charge field. The charge field simply deflects photons in the gap down here, and it deflects red ones the most. But this doesn't explain the amount of shift. "Why is red shifted to yellow?” Why not orange? Why not green?

The whole explanation is in the relative energies of charge field photons and visible light photons. We know the energy of visible light photons: it is in a narrow band in the E/M spectrum, centered around 500nm. Well, charge photons are also real photons, with real energies, real wavelengths, and real frequencies. I have shown that charge photons have an energy that peaks in the infrared region, with a wavelength of about 2 x 10⁵nm. This means charge photons have an average energy about 1,000 times less than our visible light photons. Because charge field photons have a definite energy relative to red photons or violet photons, they will move those photons a certain amount, but no more. It doesn't matter how long they are in the field.

We will pause to notice that this explains why red is diffracted more than violet [in Goethe's first illustration, the yellow band is wider than the blue band: this was noticed by some but never explained]. Charge photons are nearer in energy to red photons, so they can affect them slightly more strongly.

The charge field cannot push red past yellow, because the charge field photon has a definite energy with respect to the red photon. The charge photon therefore has a calculable maximum field effect on the red photon. Since the hole in the wall creates this maximum effect, we may establish that the maximum is easily reached, and, in almost all cases, will be reached.

Now let us do the same analysis on the top edge and the violet photon. We can see that, mutatis mutandis, the charge field will also have an effect on the violet photon. But why are the upper photons deflected up in Goethe's illustration? Shouldn't the charge field of the wall push them down? No one, including Goethe, can tell us. The charge field gives us the simple answer once again. The charge field emitted by the edge above is emitting down. This makes that charge field in opposition to the charge field of the Earth, which is moving up. But when the photons clear the gap, they are back in the charge field of the Earth, which pushes them up. They have more charge beyond the gap than they had in it, so they bend up.

But using this logic, shouldn't the photons also go up after they clear the prism? Aren't they re-entering the Earth's charge field there, which is moving up? Yes, they are re-entering the charge field of the Earth only, without the charge field of the prism. But they are moving from a field with more charge to a field with less charge. In the prism they had Earth+prism charge. Beyond it they have only Earth charge. So the photons are moving into less charge, and fall.




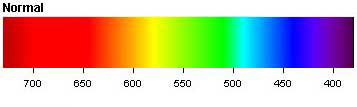
Let's study this illustration once more. This is what proved to me that yellow and cyan were special. This second illustration from Wiki also shows it clearly. First, notice how narrow the yellow band is in both. It has always been known that yellow is much narrower than the other primaries or prismatics, but we never hear about it. We have to discover it for ourselves. Many charts or illustrations actually falsify the yellow band, showing it much wider than it really is. While green and blue spread across 60nm each, and red spreads across at least 100, pure yellow is found only at 570, in a band little wider than an absorption band. Even more strange is cyan, since we are never even told it is on the spectrum. Newton didn't list it as one of his seven prismatics, and Wikipedia still ignores it as if it isn't there. All lists go straight from green to blue, but cyan is sitting there plainly, a perfect bookend to yellow. Like yellow, it also has the appearance of a narrow band, almost like an absorption line at 490. These two illustrations show it clearly, but most charts falsely omit it, not only by mention but by fact: they don't even paint it in.

Another thing to notice is that the spectrum from Wiki creates a false circle, as if red were both at the top and bottom of the spectrum. This allows them to create magenta by combining red and violet, but in the real spectrum, magenta is not included. The violet of the natural spectrum is a dark violet, as in the first illustration, and so magenta cannot be created. The third leg of the cyan/yellow/magenta triad is not on the prismatic spectrum, which is a real problem in connecting colorimetry to the prismatic spectrum. Colorimetry can only be achieved by creating a circle where in nature there is only a line.

Goethe showed that nature actually helps us here, since what I am calling nature is only Newton's nature. The linear prismatic spectrum of Newton is just one possible spectrum out of several. We saw above that nature does create magenta: it just needs objects to do it instead of gaps. We need to consult and combine all these natural spectra to create the color circle and colorimetry. Newton's prismatic spectrum won't do it alone.



One last question to answer before I conclude this section. Why is blue plus yellow sometimes white and sometimes green? We already know the answer, in part. When our color fields are additive, we get white; when they are subtractive, we get green. The only problem here is that both Goethe's experiment and Helmholtz's seem to be additive. If we project yellow light and blue light, we get white light. What is the difference between that projected light and the light diffracted by Goethe's slit? Well, let us return to the Wiki photo of the projected light. We are in a dark room and the light is projected onto a WHITE wall. We aren't looking at the rays of light themselves, as we would be in a diffraction. We are looking at the light reflected from the white wall. The wall, being white, is capable of reflecting all the light. It doesn't absorb it. That's why the situation is additive. But with Goethe, we are seeing the light in the air itself. The air is like a clear transparency. When you superimpose transparencies, the situation is subtractive, as we see from the other photo at Wiki. So Helmholtz's experiment was not a disproof of Goethe's. In reflection from a white wall, blue and yellow make white. In refraction and diffraction in air, blue and yellow make green.

After all this, I will be told that we know green is a primary from the light mixing experiments. We can see green come out of the projector, mix with red, and yellow is created. Therefore we know immediately that green is primary and yellow is secondary. But that is jumping the gun. Why should that experiment take precedence over Goethe's? Because his experiment was done 200 years ago with simple objects, and this newer experiment takes place with a fancy projector, does not mean the newer experiment is right. Goethe would simply point out that the light coming out of the projector is already a mix of yellow and cyan. When it is crossed with red, the red cancels the cyan, and the primary yellow is left standing alone. Modern theorists always stop the analysis when it suits them.

It is claimed that Goethe would reject both the particle and wave theories of light, but this is not true. Goethe said that color was neither wave nor particle; he did not say that light was neither. Goethe's theory was not mainly a theory of light, it was a theory of color, and he never attempted to use his data to show that light was a particle or wave. His differences with Newton were nothing to do with the composition of light as material; his differences were to do with the way light interacted with material and with the eye. Goethe had no need to either reject or confirm waves or particles, since the composition of light was not his concern. His concern was the action of light, and he wanted to show that light did not even act as Newton had claimed, regardless of its composition.

Since I have made apologies for Goethe, I will also make them for Newton. Interestingly, Newton explained the different bends in the prism by the varying spins of his corpuscles. Huygens and Hooke both took exception to this, since it seemed to contradict a wave model they felt had already proven. Turns out Newton was right, though, since I have shown that the wavelengths of photons are indeed caused by spin. Both Huygens and Newton were right, since the wave model is also true, and Newton was correct in his demonstrations that his theory worked equally well for light as waves. It worked equally well for spins and waves, since it was the spins that were causing the waves. There was a wave/particle duality even then, and if it had been well understood that the wave belonged to each photon, instead of to some medium, we could have avoided centuries worth of feuding. Unfortunately, the feud continues, since mainstream physics still has not recognized that the wave/particle duality is not really a duality. The photon is not “sometimes a wave and sometimes a particle,” it is always a particle with an intrinsic wave, caused by a simple stacking of spins.

Although I have shied away from modern colorimetry in this paper, one of the proofs of my new theory comes from Maxwell. Maxwell is in many ways the father of modern colorimetry, and our trust in RGB, and therefore in green, comes from Maxwell. Maxwell based his theory on the work of Young and Helmholtz. At first Young had chosen yellow as his third primary, but he changed his mind and picked green in the end. Maxwell also chose green as his third primary, due mainly to an acceptance of Young's earlier choice. The argument of green or yellow has been made moot in the 20th century, with the understanding that all colors can be made from either RGB or CMY. Green works because it contains yellow. As we have just seen, RGB are the big patches on the spectrum, and CMY are the thin lines between them. Either can be used to represent the full spectrum. But the problem Maxwell came across is that certain colors, although matchable in hue, were not matchable in saturation. For example, it was found that gamboge yellow could not be be matched no matter how much green and red you stacked. Modern theories try to hide or downplay this finding, but it is clear evidence in favor of yellow over green. Modern theorists explain it this way:

This was a crucial step in the development of color science, because primary colors no longer had to be real colors, that is, paints you can actually spin on a color top or lights you can actually extract from the spectrum. Even though this seems to make no physical or perceptual sense, it reflects the fact that the mind never sees the cone outputs and therefore our visual primaries are imaginary colors to begin with.²

That is a clear dodge, since it doesn't begin to address why we see higher saturation. Remember, the imaginary colors are less saturated, since they are the ones we can create with Maxwell's mixes. But we don't see these imaginary colors, we see the highly saturated real colors. Therefore it must be false that “our visual primaries are imaginary colors.” If our visual primaries were imaginary colors, then we could not see the high saturation of gamboge, for the same reason colorimetry cannot create it.

It is easy to explain gamboge if we can just keep adding yellow. Gamboge is a problem only for those who have green as a primary. This same author also says,

But faulty artists' ideas were only a sideshow in the history of primary colors.

You know I cannot let that pass. It is true that faulty artists' ideas were only a sideshow in the history of primary colors, since it is faulty scientists' ideas that have caused all the major problems, and that have defined the flawed theories we currently keep.

But to get back to it. Yellow is not the only color whose saturation cannot be matched by RGB. Two others, not surprisingly, are cyan and magenta. Using RGB, we find that even some greens cannot be matched. Why? No one knew before now, but I can tell you it is because you don't have yellow to add by itself. High saturation can only be achieved by CMY, not by RGB. You need the pure colors to start with, and RGB colors are already mixes. A correct colorimetry would be based on CMY, not RGB.

I have rehabilitated Goethe to a certain degree, but I must look at some ways that he fails. It has been said even by his detractors that you can always trust Goethe's experimental reports, but I did not find that to be true. It may be that my eye is more practiced than that of most people, but I could not convince myself that the black circle in the white frame looked smaller than the white circle in the black frame. This is Goethe's first illustration, and it is still reproduced today on the web as a common optical illusion. But that is relatively unimportant compared to another fault I found. Goethe states that the blue at the bottom of a candle flame will not appear blue against a white background [159]. I performed the simple experiment and found that I could still see the blue. This is important because it falsified the classical explanation of blue and yellow as produced by a “semi-transparent medium.” Goethe repeats [156] the claim of Leonardo that distant mountains appear blue because we have a semi-transparent medium on a dark background. A semi-transparent medium on a light background is yellow. Leonardo and Goethe use this same explanation for the blue of the sky: space is the background of this semi-transparent medium, and space is dark. It is wonderful that Leonardo understood that space was dark behind the daylight sky, but his explanation (and therefore Goethe's) fails. If it were true, then the candle-flame experiment would be as Goethe said: we would no longer see the blue. Since we do see the blue in the candle even on a white background, the blue cannot be caused by the transposing of the foreground and background. The blue is caused by the flame itself.

Basically, this one fact dooms a large part of Goethe's theory of dioptrical colors. We cannot give the nod to Newton here, or to current theory, since current theory still cannot supply us with the correct answer to why the sky is blue or why distant mountains look blue. We are sent to the Rayleigh or Mie equations, and given some squishy answer about scattering, but but the real answer has to do with green again. Actually, distant mountains can look either purple or blue, depending on whether they are covered with trees or not (“purple mountain majesty,” you know). If the mountains are covered with trees, then they are green locally. They may already be blue-green locally, if we are dealing with conifers. In that case, they look blue from a distance simply because the yellow in the green has been scattered. I have shown that longer wavelengths are scattered preferentially by the atmosphere, not shorter wavelengths. We see color because it hasn't been scattered, not because it has. Therefore, if we are looking at light that was originally green, the more it is scattered the less yellow it contains.

Likewise for mountains that aren't covered in trees. In that case, we are looking at rock, which is grey or brown. If you scatter the longer wavelengths out of grey, you get purple.

I have shown where Goethe was wrong, but where he is was right is even more interesting. I have shown how to analyze light entering a dark room through a slit and so on, but Goethe's primary critique of Newton concerned light being split without any edges at all. He showed that dark and light areas seen through a prism could create rainbows, and no theory up to that time ever addressed that fact. No theory up to THIS time addresses that fact. Goethe shows it, but does not explain it with any photon or wave mechanics. And even my analysis above has not yet explained it. So we need another section to address it.

To prove that it is real, and not some illusion of Goethe, we may use more modern examples. We can use images on a computer screen to prove it, since no one denies that a computer screen is flat. A computer screen cannot have any edges within it: all apparent edges are boundaries of light and dark only. This can be seen most easily by looking at print on a computer screen. If you look at this black print through a prism, you find it turns magenta. Depending on the orientation of the prism, you also get two ghosts. If the point of the prism is up, you get a yellow ghost above and a cyan ghost below, with the yellow ghost higher than the cyan ghost is low: the yellow ghost is about a full character above, while the cyan ghost is about a half character below. If the point of the prism is down, you get a reversed effect.

If black is the absence of color, how does the prism turn it magenta? And where do the ghosts come from? How can black be split three ways, or at all, according to Newton? And why only three, and these three? Where is red? Where is green? Where is blue? If colorimetry is based on RGB, why is this split so obviously CMY? And how in the world can your brain “average” black into magenta? According to the About.com site I ridiculed above, magenta is a creation of the brain from red and violet. But we don't have any red and violet here. There is no red or violet, either before or after the prism splits the light. Without the prism, we have black and white letters. With the prism, we have magenta, cyan, and yellow. So the brain isn't apparently doing anything with red or violet. About.com can only claim that the prism is splitting black somehow into red and violet, which our brain then mixes into magenta. But that argument is easily falsified by the fact that we can see violet and red next to eachother without the brain mixing them. A prism normally splits into bands, and the brain does not normally mix or conflate bands that are next to eachother. It sees them as distinct.



Another good example is found by looking at a line of prismatics through a prism. This is best seen with small color squares surrounded on all sides by white. Looked at through a prism, all the prismatics are split into CMY. If the point of the prism is up, yellow is on top. If the point of the prism is down, yellow is below. Yellow, cyan and magenta cannot be split by the prism or any number of prisms in a row. Green is cyan and yellow. Red is magenta and yellow. Blue is cyan and magenta. Violet is cyan and magenta, heavy on magenta. If nothing else, this proves that CMY is more primary than RGB.

These two experiments are crucial, and they prove that Goethe was on to something very important. They also prove that current theory is way off track. They also prove that current rainbow theory is completely off track. Let's return to the first experiment, where black print surrounded by white is split into CMY. We have two things to explain: 1) why is black split at all? 2) why is yellow following the point of the prism?

The second of these two questions is the easiest to answer. Yellow is nearer the point for the same reason red was in the explanations above. The yellow photon has less energy than the cyan photon, so it gets diverted more by charge. Turning the prism upside-down also turns the charge field inside the prism upside-down, so the effect is reversed. The photons simply follow the charge field.

The first question takes us into new theory. It isn't the black that is split, it is the edge between black and white that causes the split, just as Goethe said. To show this, we return to my rainbow theory, which says that Alexander's Band causes the rainbow, not the rainbow that causes Alexander's band. The bands of dark and light create the possibility of a color split, which the moisture in the air then causes like the prism. To prove this is so, just look at this illustration through a prism:



I have simply drawn a main grey band, with a white line below. This creates the right rainbow, with the colors in the right order. This extends my theory in the rainbow paper a bit, since I did not mention the line below there. Doing this experiment proved to me that Alexander's main band was not enough. We also require small secondary bands above and below, and I hypothesize that these are also caused by the Solar corona, in a straightforward manner. I am certain that by studying the corona more closely, we will find them and their cause. They have been invisible due to their narrowness: in rainbows they are completely engulfed in the color bands they create.

You will say that the secondary bow is not created in my illustration, and that is true. It is impossible to create the reversed secondary bow in the right order on a piece of paper, since the gravity field is present with the rainbow and it is not present in the same way in a piece of paper. The unified field certainly exists in and around the paper, but it works differently than in the atmosphere. To be more specific, the image on the paper is caused by reflection. But the image of the atmospheric rainbow is caused by rear projection, as I showed in my first paper on rainbows.

Regardless, my use of grey bands conflicts very aggressively with current theory, since we find that it does not matter what color grey we use. Only the relative tones or values matter. We can let the grey be a red grey, a green grey, a blue grey, or a purple grey: the splits are not affected. It is not the colors in the grey that matter, it is the relative densities of photons, as I am about to show.

Not only does this prove my rainbow theory, it proves my photon theory. I have said that we start with red and violet photons, which are then shifted into yellow and cyan. All else is a mix. To show this most clearly, we start with a thin horizontal black line. Just draw such a line on a piece of paper or in Photoshop, and look at it through a prism. Yellow is shifted up and cyan is shifted down, and the line itself turns magenta. Magenta is not one of my photon primaries or shifts, so where did it come from? Well, this experiment shows that magenta is not really in the same category as its friends yellow and cyan. Magenta is part of the CMY trio, but it is created in a different way from the other two. The top edge shifts yellow up and red down (for reasons I will show in moment). The bottom edge shifts cyan down and violet up. The violet and red superimpose to create magenta. They don't average, they stack. This is not so different than current theory, except that current theory never addresses shifts caused by dark and light alone, or edges not created by materials. As Goethe said, we have diffraction caused by non-material edges.

We can see even more clearly this is what is happening by widening the line. We double and triple the width with no effect, but if we take the width up to about a quarter of an inch, we start to see red and violet bands instead of magenta. The black in the middle is too far from either edge, and the color can't be bent enough to overlap.

So our final question is, How does the non-material edge create the split? Well, it doesn't, of course. The prism creates the split. The line only creates the possibility of the split. How does it do that? One thing to notice is that it depends how far your prism is from the edge. If you take your prism quite close to the edge, there is very little or no split. As you back away, the split increases. Why? We will assume for the time that it is because the edge becomes more diffuse at a distance. As the photons travel away from the paper, they mix, destroying any crispness the edge originally had.

You will say that this explains nothing, and that is true until we look closer. We have no charge field variation here to explain anything, so we are in new territory. All my theory above is out the window. But the assumption of diffusion leads us to the correct answer: the variation in the photon field acts like the variation in the charge field, creating the same effects. All we have to do is remember that the grey field or dark line has fewer photons than the white field, therefore the white field is emitting a greater photon density. We have density variations we can use here, just as with the charge field density variations above. Since photons in my light theory are real particles with real mass and radius, they create real densities. So even in the absence of a charge field, we have density variations due only to dark and light.

And that leads us to a further realization. My last illustration (of the grey rainbow) was done on a piece of paper, then scanned, but it could have just as easily been done in Photoshop. Either way, we have a surface reflecting or emitting variable amounts of light. But that surface is also particulate. A surface is a thing, and all things have charge fields; so we are not without a charge field here. Can we postulate a charge field variation then, with grey bands on a piece of paper? Yes, we can. Let us start with a white sheet of paper. The charge field is pretty equal and stable across the sheet, since the sheet itself is not variable. Likewise for the light hitting it. If we see the sheet as uniformly white, the incoming light is not variable either. What happens when we draw a grey band on the white sheet? The reflectivity of the sheet is altered, and more photons are absorbed. This means that the charge field in the grey band is being tamped down a bit. Not only is the reflected light less dense in that area, the emitted charge field is less dense. So we have a double variation to work with.

This means that we do not need material edges to cause diffraction or refraction. Edges of dark and light also work for the same reason. All we require is density variations, and we have shown those in both cases. This is what Goethe was noticing when he first scanned his room with his prism. This is why he knew Newton could not be right. Goethe could not explain the mechanics underneath the diffraction he saw, but he was quite thorough in cataloguing the effects. He saw that Newton's theory of bending was very incomplete, since it could in no way explain refraction by non-material edges. To explain refraction and diffraction mechanically requires the unified field and density variations, variations Newton did not have.

To see how this new theory of light applies to new problems in physics, you may now visit my paper called "The Laws of Refraction," in which I analyze and correct an experiment from Harvard SEAS.

I have now discovered much more about these questions, which you may read about in my newer paper entitled Cool Moonlight. There we see how antiphotons must be considered in color theory.

¹http://www.handprint.com/HP/WCL/goethe.html
²http://handprint.com/HP/WCL/color6.html
*http://www.buzzle.com/articles/color-spectrum-chart.html
**http://chemistry.about.com/od/colorchemistry/f/how-magenta-works.htm. By Anne Helmenstine.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.