return to homepage THE VIRIAL THEOREM The virial theorem comes from the math of Lagrange, as extended by Clausius. The historical and current derivation starts with the moment of inertia, so the virial must apply to a collection of particles arrayed about a center. That is, it applies to circles or spheres.
Now, the virial derivation finds that ΣFr is the potential energy of the system by actually deriving it and assigning it, but that is just one more fudge. Remember that they found
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.
return to updates
IS FALSE

Nothing does more hurt in a state than when
cunning men pass for wise (Francis Bacon)
I = Σmr2
That is a summation of all the individual moments of inertia of N number of “point” particles in our collection. Notice that m applies to the mass of each point particle. Our first question here is, “How can a point have mass?” It can't, but we will move on, since we have much more important and obvious fudges to show. The virial G is then defined as the sum of the motions of these masses:
G = Σmvr
That expression looks like angular momentum, L = mvr, but it isn't. Beware. The v has not been defined as a tangential velocity. The v there is found by differentiating r, and you cannot differentiate r to find a tangential velocity. Rather, Lagrange, the inventor of this derivation, then relates the two equations:
G = dI/2dt = Σmrdr/dt
We have a huge cheat right there, which I will analyze below. Not satisfied with making a distance into a velocity, he then “differentiates” again:
dG/dt = Σpdr/dt + Σrdp/dt = Σm(dr/dt)(dr/dt) + ΣFr = 2K + ΣFr
Where K is the summed kinetic energy of the system. You can see that he has “differentiated” twice to turn a distance r into a velocity squared. That allows him to to end up with a force F at r and a kinetic energy.
But let's unwind that mess. It is a horrible fudge from beginning to end. We start by noticing that r is just a simple distance in the first equation. It is the distance from the center of some “point” particle among N point particles in our rotating system. Lagrange wants to turn that distance into a velocity, so that he can create a momentum. He needs mv, you see. So he takes the “time derivative” of r.
I have said that calculus is misunderstood1 and misused, and this is another perfect example. I entered this problem thinking I was only going to have to make a correction based on my correction to the angular momentum equations2, but my work on the calculus is paying off, because I can now show that this is fake calculus. Lagrange is pretending to do calculus, but he is just finessing equations. Amazing that no one has had a problem with that for 230 years.
When you actually do real calculus and you find a real derivative, you are differentiating a curve or an acceleration. You are finding the rate of change of that curve or that acceleration. But you can't find a rate of change of a distance r, since there is no change. In other words, you can't differentiate r with respect to t in this problem, since r is not changing with respect to t. Just think about it physically for half a moment. The distance r is defined as the distance of point k from the center at time t. Now let some time pass. Has the distance r changed? The current derivation has nothing to say about it, but we can't assume that r is moving, much less accelerating, since that would mean all our particles in our system are swapping places at a fantastic rate. Maybe they are, maybe they aren't, but this system has not been defined as a gas, remember. The virial theorem is now used on stars, dark matter, white dwarfs, and so on, and in stars there is no reason to believe that matter in the star is changing its radius over time. Is the core of our Sun accelerating out into the corona, or vice versa? And if it were, wouldn't all this motion have to offset? All the motions of all particles k would have to sum to zero, or the star would be exploding, would it not? In other words, the distance from center r cannot be changing, as a sum. If our system were a gas, the same would apply: the total change in r over time could not increase, or our gas would be expanding very quickly.
I have been told that of course a particle in circular motion has an acceleration, which is the centripetal acceleration. Lagrange wasn't proposing particles just sitting in a circle. They have a moment of inertia, which means there is a centripetal acceleration (usually understood to be gravity). That sounds logical until you remember that a centripetal acceleration doesn't change r, unless we are in some sort of gravitational collapse or explosion. Whether the particles in question are orbiting, or, like the particles that make up the Earth, are part of a spinning structure, r is constant. Therefore my analysis remains. If r is not changing, you cannot differentiate it, not twice or even once.
This is all just to say that r cannot be taken to be changing with time. Lagrange has just buried the mechanics here, and the math is unsupported. Unless he can show that the distance of every particle is increasing to some power with time, he cannot differentiate r.
Besides, in the moment of inertia equation, any velocity is a tangential velocity. Just look at the definition of the virial. The virial looks just like a summed angular momentum, in form. The angular momentum L is equal to mvr, and so is the virial. Well, the velocity in the L equation is a tangential velocity. In circular motion, the value of the velocity does not change over time, since the tangential velocity is determined by the distance r. If r is a constant, then v is a constant. I have just shown that we cannot be letting r change with time, either as a velocity or as an acceleration; therefore, v cannot be changing either.
You can't turn any distance you like into a velocity just by finding some nebulous “time differential”. You can differentiate a distance into a velocity only if you have a variable velocity: an acceleration. If your velocity is either constant or zero, you cannot differentiate a distance, since there is no variance. There is no change with time to study or represent with math. In the case of the virial, we have the appearance of a tangential velocity which is constant, but even that is not what the equation is representing, as I warned above. The first equation is written with respect to r, which is not changing at all. Therefore, the “velocity” of the distance r is zero. We have no velocity here at all. The math above is just magic.
But the problems don't stop there. Lagrange has also cheated magnificently in finding that the derivative of r2 = 2rdr/dt = 2rv. The term dr/dt there is just notation and cannot be substituted for a velocity variable. In this place, dr/dt can be thought of as a velocity only if it is the velocity 1. This is because Newton and Leibniz both intended for this notation here to be taken as a dimensional constant, not as a velocity variable. We must assume that a great mathematician like Lagrange would know that, so that we have caught him in a very big push here. To see a more extended analysis of this cheat, you may go here.5
And there is even more fudge. Every line is a new cheat. Look here:
dG/dt = Σpdr/dt + Σrdp/dt = Σm(dr/dt)(dr/dt) + ΣFr
In the last term, we find that F=dp/dt. Funny that Lagrange never has to concern himself with angular momenta here, even though we are in a circle or sphere. His virial G is written as a summed angular momentum, but he and the historical derivation don't want you to notice that. I have pointed it out, but textbooks never do. To have a moment of inertia, you have to have some rotation, so we cannot imagine that our collection of points here is just static, arrayed around a center. If that is so, then why is the virial expressed with p and v, instead of L and ω? F=dp/dt is a linear equation, not an angular equation. In an angular solution, we would have T = dL/dt. We would have a torque.
The reason this derivation ignores all this is that it wants you to think the velocity in the equation G = Σmvr is defined in some way, when in fact it isn't. The virial equation doesn't write the angular velocity as ω, because if it had you would have recognized for yourself what I just recognized. You would have seen that you can't differentiate a radius r into a ω. No, dr/dt ≠ ω. The virial equation is given us right after the equation I = Σmr2, so we think the v is like the velocity in L=mvr. But as I have shown, the v is actually obtained by differentiating r, and r implies no motion of any kind, neither a tangential velocity nor an angular velocity, nor any other change of r.
Also, the v in the equation L=mvr is not found by differentiating r, as you will realize if you think about it. In that equation, it is clear that change-in-r cannot be causing v, since r is not changing. Historically, what is thought to be causing v is an “innate motion.” Or at least that is what Newton told us. He assigned the tangential motion to an independent linear motion, and that motion became curved by the influence of a centripetal acceleration acting upon it. This must mean that differentiating r to find a velocity is a double and triple fudge, worthy of the all-time hall of fame. Lagrange has pushed this derivation in every single line.
I came in expecting to correct the equation L=mvr, but that equation never raised its head. The virial derivation had to drive right around L, because the virial is just a variation of L, and no one wanted you to realize that. If the virial can be written as a sum of kinetic energy and torque, why can't the angular momentum be written that way? If we sum L and then differentiate, will we find the same thing? No, because the v in L=mvr is defined as the tangential velocity, and the v in the virial is undefined. That is also why the force at r can't be defined as the torque: in the torque equation, the velocity is defined as the tangential velocity. In the virial, the velocity is undefined. They don't want to connect Fr to the torque, because they want to connect it to the potential energy.
All this is swept by very fast in the derivation, since historically they want to bury that velocity as quickly as possible. The virial is now commonly written without any mention of a velocity, as in Lagrange's identity:
dG/dt = d2I/2dt2 = 2K + V
where V is the potential energy of the collection. Which of course leads us to the Lagrangian. But this means that the virial and the Lagrangian are meant to be applied to gravitational systems. That is why they are interested in potential energy rather than torque. That is why spin is ignored: they want to be able to apply the equation to gravity fields, spinning or not.
That, of course, confirms my initial analysis. If these energies are the result of a gravitational field, then the distance r of particle k from the center cannot be accelerating over time. The particle k may be feeling an acceleration, but it cannot be accelerating, short of some revolutionary new postulate. For instance, I could be defined as some particle k in the field of the Earth, since, relative to the Earth, I am pointlike enough. But my radius r is constant. It cannot be differentiated with respect to time, can it? If we differentiate my position r with respect to time, we will find pretty much zero. We could say the same of most objects in the Earth or in its field. Only objects in freefall could fit into the virial equation. Since a star is not a collection of objects in freefall, I do not see how we can apply the virial equations to a star.
The virial equation and Lagrange's identity have also suffered from another big disclarity. Physicists have always wondered where that 2 comes from. Why don't the kinetic energy and the potential energy offset exactly, as they should? Why is the potential energy twice the kinetic energy? If we look at the definitions of potential and kinetic energy, the two should offset. One should be the opposite of the other, and all we should need is a minus sign to create the equality. By the work-energy theorem, kinetic energy is Fd. By the definition of gravitational potential energy, we find V=mgh. Since F=mg, this becomes Fh. The variables h and d are equivalent, since in one it is the distance the object travels, and the other it is the distance the object would travel, if released. So we should have an equality. If the potential energy is twice the kinetic energy, then why doesn't the object in the field have half its energy left after it falls to center? I will now show you the cause of this gigantic error.
An even simpler derivation of Lagrange's identity goes like this:
-V = GMm/R
F = GMm/R2
C = ma = mv2 /R
where C is the centrifugal force
GMm/R2 = mv2 /R
K = mv2 /2 = GMm/2R
2K = -V
The problem there is in the third equation. I have shown3 that a ≠ v2/R. Instead, a = v2/2R. Yes, unbelievably, Newton made a simple error in his versine proof, and that error has never been corrected until I found it. It has been “confirmed” by all physicists and mathematicians since Newton, and re-expressed with modern calculus. However, the calculus is forced to fudge the equation in order to make it match Newton's equation.
If we make the correction here, we find that K= -V, as it should. There should be no 2 in the virial, and no 2 in Lagrange's identity. In this way, we can see that the proof has been pushed in yet another way. The longer derivation at the beginning can't be correct, since we now know it was pushed in order to find that 2.
[You may now go to my new paper on the Lagrangian, where I analyze it in greater detail. I also analyze Lagrange points there, showing that they are at the wrong place in the field.]
Now let us make the other corrections to the virial. The virial equation can't be derived from the moment of inertia, because we want to apply this to a gravity field that is not spinning, if we like. With no spin, you have no moment of inertia. A critic will say that the standard model is not bothered by the requirement of spin, since all stellar and quantum objects seem to be spinning. But that is not the question, is it? The point is that in a gravitational field, neither the kinetic energy nor the potential energy needs to be caused by spin. Neither Newton's nor Einstein's equations require spin to express gravity. Therefore, we should be able to develop a virial equation with no spin. We could add spin later, if we like. Besides, the current derivation says nothing about spin, and the spin is never included in the equations. If we had spin, the current virial equation would have to include a variable for it. It does not. If we have no variable for the rate of spin, then we cannot possibly derive the equation from the moment of inertia. Remember, the v in the virial is not the rotational velocity or the tangential velocity. No, it must apply to some radial change in r. Therefore, the virial contains no spin. If it contains no spin, it cannot have a moment of inertia and cannot be derived from a moment of inertia.
We really have to start over from scratch. The virial theorem is said to find (Wiki), “a general equation relating the average over time of the total kinetic energy of a stable system bound by potential forces with that of the total potential energy.” We see in that definition that we are dealing with a gravity field, since what other object arrayed around a center is “bound by potential forces”? To find a summed kinetic energy in such a field, we have to assign a velocity. But if the field is not spinning, what is this velocity? The virial theorem cannot be measuring molecular or atomic motion, since those motions are not mainly caused by the gravity field and would not be balanced against gravitational potential energy. We are told that the virial theorem can be extended to include E/M fields, which must mean that the original equations did not include those fields. Therefore, the forces between particles are gravitational in the first instance. What motion in the field does gravity cause? Unless we are talking about orbiting or freefall, it causes none. Since a gravity field requires no tangential velocity, orbiting is not required here. And since we are not told that all objects are in freefall, we must assume otherwise. The virial should be and is applied to particles that make up a star or planet, and the particles that make up a star or planet are neither in orbit nor in freefall.
This means that without the equivalence principle, no velocity can be assigned. So let us propose that gravity does cause real acceleration in all particles in the field. We can believe that is due to real expansion, or we can believe that is due to a vector flip and some mathematical imagination. It doesn't really matter. This sort of math is used all the time now by the mainstream, as I have shown in my Pound-Rebka paper4. You cannot calculate gravitational blueshifts without assigning a motion to the surface of the Earth. For proof, I send you once again to Feynman Lectures on Gravitation, lecture 7.2.
Either way, we assign the acceleration to r. We start with the common equation v = √(2ar r). But instead of imagining this equation is caused by the particle falling toward the center, we imagine it is created by the particle being accelerated out from the center. At that acceleration, the particle would acquire a final velocity of v at distance r. The kinetic energy of the particle at r will then be mv2/2, and the summed energy of all particles will be
K = Σmar r
Since F=mar, that becomes
K = ΣFr
dG/dt = Σpdr/dt + Σrdp/dt
Then they assigned the first term to kinetic energy and the second term to potential energy. How is that even remotely logical? The first term contains a momentum and a change in r. The second term contains a distance and a change in momentum. Just because you have a force doesn't mean you have a potential energy. In my own derivation, I got a kinetic energy from a force, as you see. And the standard model derives kinetic energies from forces all the time, as in the work-energy theorem, Fd = K. Force times distance equals kinetic energy, not potential energy. You will say that is force through a distance, while we are looking at force at a distance, but after my equivalence principle analysis, the difference is not so clear. If the particles must be given a motion in the field, then it would appear we actually have a force through a distance here as well. Which means that the historical assignment is just arbitrary and willful. They assigned Fr to potential energy for no other reason than that they wanted to. But if this entire historical derivation was derived from some motion at r, and since motion is kinetic by definition, then dG/dt must be kinetic in toto. Again, they derived all this from the moment of inertia, and the moment of inertia, though a scalar, cannot be static or potential. Their entire derivation depends on motion, hence the time differentials: you cannot have time differentials without motion. Therefore, they cannot assign any part of dG/dt to a potential.
The current derivation tells us that, “The total force F on particle k is the sum of all the forces from the other particles j in the system,” and then uses that definition of force to prove that ΣFr is the potential energy. But it only proves that IF the F in ΣFr is “the net force on that particle,” then V is the sum of the potentials. Unfortunately, it is never proved that dp/dt is the net force on particle k. The derivation simply states it. In fact, it is impossible that dp/dt in that equation is the net force on particle k, since the equation contains another term, and the terms are added. Once again,
G = Σpr
dG/dt = Σpdr/dt + Σrdp/dt
As you see, we already have a sum of momenta in the first equation. Then we differentiate, which gives us the two terms. So we cannot separate the second term from the first. Forces are contained and implied by both terms, and you cannot ignore the force in the first term. In other words, it required some force to create that kinetic energy pdr/dt. K = Fd. If we have a kinetic energy in the first term, we have some force that created it. The two terms are added, so you cannot pretend that all the force is in the second term!
No, we have to find the potential energy in a different way, just as with the kinetic energy. This historical proof is compromised in every part, in every possible manner.
The potential energy is easy to derive without the virial, since we just sum the individual potential energies. The potential energy of a single particle is mgh, with h being equal to r here. So the sum is
V = Σmgr = ΣFr
The potential and kinetic energies are equal, as they must be, and we don't require big fudged equations to show it. We especially don't need to derive any of this from a moment of inertia, since a moment of inertia requires spin and a gravity field requires no spin.
What does all this mean for physics? Well, it is complete knock-out, nothing less. Because I have shown that the virial is not only derived by a big fudge but is actually false as well, the very sky falls. As just one example, Fritz Zwicky has used the virial to deduce the existence of dark matter. But I have shown the equation is 100% wrong. Kinetic energy is actually twice what we think it is, or 100% more than the equation tells us, so all cosmological estimates are off by huge margins.
The same can be said for the Chandrasekhar limit for the stability of white dwarfs. The virial radius is also compromised by a large margin. Everyone who has ever used the virial, including Rayleigh, Poincare, Ledoux, Parker, Chandrasekhar, Fermi, Pollard, Schmidt, and thousands of other top names, are not only shown to be wrong, but to be very poor mathematicians. How is it that no one has thought to check the postulates and manipulations of Lagrange for two and a half centuries?
The fall of the virial also topples the Lagrangian and the Hamiltonian, which rocks QM and QED to their cores. The Lagrangian is defined as L = K – V. If Lagrange and all subsequent physicists have miscalculated the number relationship of K and V, then L cannot be correct. K is half what it should be relative to V, which makes this equation wrong by a huge margin. And if K and V are equal to one another, then the Lagrangian is simply L = 2K = -2V. This falsifies the Lagrangian for Newtonian gravity, which falsifies Gauss' law for gravity. It also falsifies both the Hamiltonian and the action. Basically, we have to rewrite all of physics for the last two centuries.
Besides, in the simplest situation (the only situation in which the Lagrangian stays clean)*, by varying x in the integral the Lagrangian reduces to 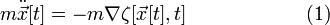
Which is just another way of writing
ma = mg
Does anyone think the action representation is really better? If you like filling blackboards and burning chalk, maybe.
Some will think that QED can remain clean of this mess, because in QED our field is not gravity. Unfortunately, the virial is thought to be applicable to E/M, and the derivation is much the same. In other words, that false 2 is carried over into the E/M equations via Lagrange's identity. Remember that the virial theorem has been generalized into many forms, including a widely used tensor form. But even in its simplest form, it is thought to be generalized. The virial theorem, as derived above, is not limited to gravitational fields. It is generalized to apply to “any stable system of potentials,” and the potentials of E/M are included in that generalization.
[You may now go to my newest paper on the Lagrangian, where I completely unlock it. I show that both the Virial and the Lagrangian are unified field equations in disguise, and that they are attempts to match my unified field equation. The variables are simply misassigned.]
[To see this analysis applied to a contemporary derivation of circular motion, you may now go to my newer paper which pulls apart a similar proof posted at Youtube. There, a physics teacher borrows and simplifies the proof of Lagrange above, and the fudges are even easier to spot.]
2Mathis, Miles. Angular Velocity and Angular Momentum. 2008.
3Mathis, Miles. A Correction to the Equation a = v2/R. 2003.
4Mathis, Miles. The Pound-Rebka Experiment. 2010.
5Mathis, Miles. The Calculus is Corrupt. 2010.
*For example, the Lagrangian in Relativity is polluted by gamma, which I have shown to be a false transform. This compromises all equations, including the Einstein-Hilbert action. The Lagrangian for Newtonian gravity, via Gauss' law, is polluted by the renormalization using μ. The Lagrangians of QED are polluted by the various unassigned constants, as well as by the unassigned field.