return to homepage
return to updates
Problems without
the Tensor Calculus
(In about 1/100th the time)
by Miles Mathis

First posted July 18, 2007
I have taught my students some wonderful mathematical shortcuts over the years, but this one is probably the most useful and the least known. In fact, I am not sure it is known at all, and so this paper. It is a mathematical manipulation only and has no necessary physical meaning, but it confirms the postulates of Einstein in a beautiful manner nonetheless.
The postulate that supplied me with this shortcut is the famous equivalence postulate, which states that gravity and acceleration are mathematically equivalent. In his lovely elevator car in space, Einstein showed that there is no difference between acceleration up and gravity down. After reading this, I decided to take Professor Einstein literally, and I reversed the vector by hand in several famous problems. This vector reversal had the mathematical effect of turning the field equations inside out. The objects in the field got larger with time, but the space around them reverted to a rectilinear or Euclidean field. In this field I could do very simple math, achieving the same numbers as Einstein. Then, when I was finished, I just turned the vector back around, to suit myself.
To show you how simple it is, I will solve both of General Relativityís most famous problems before you get to the end of this pageóand you will understand the solutions, too.
The first problem is the precession of the perihelion of Mercury. Einstein told us this was caused by extra curvature from the Sun, so I will solve by looking at light move from the Sun to Mercury. Like Einstein, I assume that any influences from the Sun will move at the speed of light. And I assume that the curvature will reveal itself through the gravitational field. To get this revelation, I just let the Sun and Mercury accelerate at their own known rates, and watch the curvature.
Since the light moves from Sun to Mercury, the Sunís acceleration happens after the emission, and is not part of the math. We only need to look at Mercuryís acceleration. Once we turn the vector around, Mercury will move in all directions, but we need to look at only one of them. We look in the direction of the orbital motion, which is tangent to the Sun. This one motion will show us the curvature, as you can see in the diagram.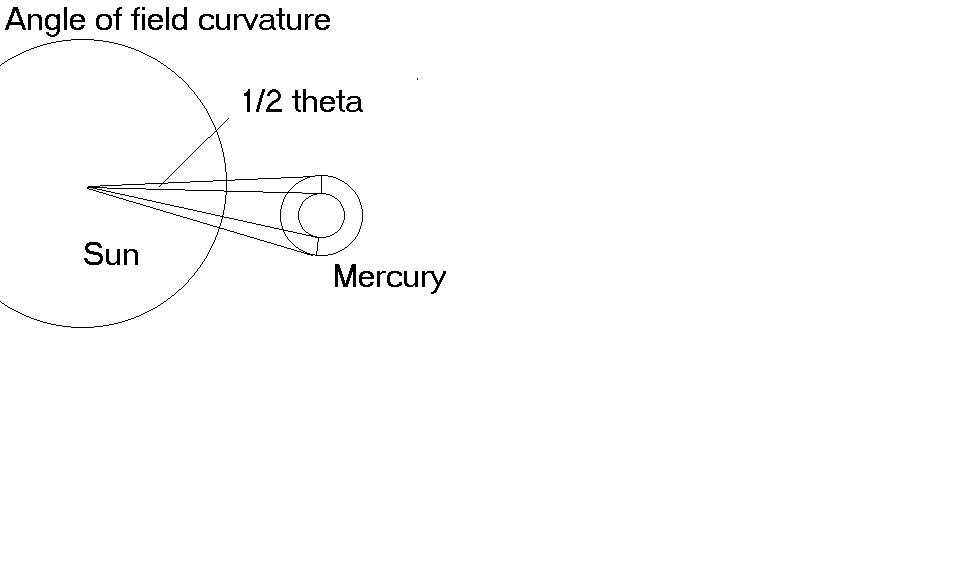
At perihelion, Mercuryís orbital distance is about 46 million km. Light travels that distance in 153.3s. The acceleration at the surface of Mercury is 3.7m/s2, so we find that one surface of Mercury will travel this far while the light is in transit:
s = (3.7m/s2)(153.3s)2/2 = 43.5km
That gives us the field curvature in one direction, but we want the total field curvature. The orbit has extension both +x and Ėx in the field over each dt, so we must double our number. Then we just find the angle of curvature created by the total acceleration in that time.
tanθ=87,000m/4.6x1010m
θ = .39 seconds of arc
If we use the mean orbital distance instead of distance at perihelion, we get .49 arcsec. Einsteinís field equations use both distances, since precession occurs at perihelion, but the curvature occurs over the entire orbit over a year. This is why his number, .45, just about splits the difference.
If you think that was a coincidence, watch the same solution applied to the bending of starlight by the Sun. We let the light pass the Sun and then travel to the Earth, where we see the bending. To calculate the amount of bending, we note the time it takes for the light to get here from the tangent, which is 501s. Once again, we reverse the acceleration vectors, but once again the Sunís acceleration happens after the light has passed. So we just look at the Earthís acceleration in 501s.
s = (9.78m/s2)(501s)2/2 = 1,230,000m
tanθ=1,230,000m/1.51x1011m
θ = 1.68 seconds of arc 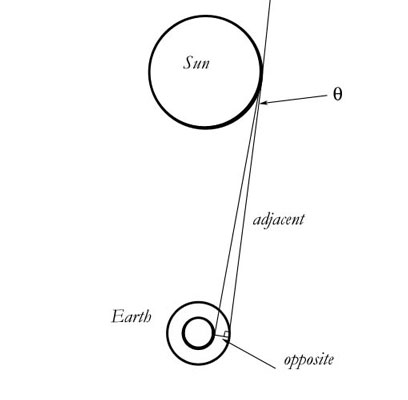
This is very near the number Einstein got (1.7), and this time we get the right amount without any doubling, since we donít need the entire field curvature here. Bending and precession arenít the same phenomenon. Mercuryís light is getting bent in both orbital directions, since the planet as a whole is experiencing precession. But only the observer on the Earth is seeing the bending, so once we reverse the vector, it is his experience that is bent, not the light. As you can see from the diagram, the light is not curving. Only his measurement of it is. Since the observer is only on one position on the Earth, the bending uses only half the field. In order to see the curvature of the whole field, the observer would have to be on opposite sides of the Earth at the same timeóan obvious impossibility.
[To see why this number does not match the current number 1.75, go here. I show that gamma causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.]
All other General Relativity problems can be solved or estimated with this method, but I will let you discover that on your own.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.