return to homepage
return to updates
LENSING
by Miles Mathis

No matter how much evidence I present for my unified field or against the standard models of gravity and E/M, my critics prefer to ignore everything I have said up to now and concentrate on things I haven’t yet discussed. Physics is such a huge field that they feel confident in their ability to misdirect the argument forever. In this, they are probably right. As long as they want to run, they can keep finding new places to hide. But they miscalculate in one important way: every new hiding place they find gives me another chance to exhibit my targeting systems. With each new round in the game, my weaponry is made to look more and more formidable, and their caves are made to look less and less sheltering. Always they must search for deeper and darker dwellings.
Gravitational lensing is another of these shallow caves. Although lensing has been around as a theory since Chwolson’s mention of it in 1924, it wasn’t “confirmed” until 1979, with the so-called Twin Quasar
Q0957+561. The Twin Quasar has many problems as the proposed effect of a gravitational lens, beginning with the fact that no one knows what a quasar is. This “quasar” has a redshift of 1.41, which, following standard procedure, would put it at about 8.7 billion lightyears. But that is assuming this quasar has no velocity relative to universal expansion, which is a very big assumption. This means that the real distance of the lensed object is unknown.The lensing galaxy has the same problem. It is said to be about 3.7 billion lightyears away, but that distance is just as theoretical. We don’t know the local velocity of the galaxy. But even if we did, our ability to measure at that distance is poor. Our ability to measure within our own galaxy is poor, as astronomers were forced to admit in 20062 when mainstream news sources dropped the bomb that we were off at least 15% in ALL distance measurements. If we were 15% wrong about nearby objects--objects about which we know much more--then these distance estimates at billions of lightyears must be taken with a grain of salt.
All this is very important, because it means that gravitational lenses aren’t offered as proof of light bending by gravity, they are offered as possible examples of bending. To stand as any sort of proof, we would have to have some math. But without distances, you can’t have math. We are never told what the gravitational forces are, because we have no idea.
Another problem is that the two images of the Twin Quasar combine with the lens in a very strange way. We are told that the lensing galaxy lies almost in line with the B image of the quasar, being only about 1” off. That is strange because we would expect both images to be about the same distance from the lens. To get a lopsided bend like this, the lensing galaxy must be highly uncentered, as a gravitational object. But normally galaxies are not uncentered. In fact, every galaxy I have ever heard of is highly centered. You don’t find galaxies where the center of the galaxy is off over near one edge. Nor can you tilt a galaxy so that it becomes uncentered from a distant perspective. As it turns out, the lensing galaxy here,
YGKOW G1, is an elliptical galaxy, class cD, which doubles my argument. Elliptical galaxies are very homogeneous, even moreso than spiral galaxies. They don’t even have arms where mass can congregate. Although they are not thought to have as much mass in the core as spirals, they are at least as centered. I think astronomers would be shocked to discover an elliptical galaxy with a center of mass near one edge. From the mainstream itself: “Ellipticals were identified by their diffuse edges, lack of structure, and generally round shape.”1The current theory recognizes this problem and tries to address it by proposing that globular clusters around
YGKOW G1 contribute to the lensing. In this way, the lopsided bends are actually multiple bends. The light is funneled through a veritable pinball machine of bends. Once we get to this point, the theory can contain any data. You can assign any bend you see to any object you like, and the content of the theory approaches zero very fast. With the predictions of Chwolson and Einstein, the far object needed to be right behind the lens, but now that the standard model has gone in search of proof of the theory, we find that the angles are no longer important. Any lopsided bend can be forced to match the theory by adding secondary and tertiary lenses after the fact.That
YGKOW G1 is an elliptical is problematic in another way. We have a doubled image here, but we would expect very nearly a ring of images. Light from the quasar is emitted in all directions, so it must be passing the galaxy all around. This was the original prediction, of both Einstein and Chwolson. Although YGKOW G1 is not perfectly circular, we would still expect large arcs of image, not just two distinct images. If the theory of lensing were true, we would expect two distinct images only under very specific circumstances. The lensing galaxy could not be an elliptical galaxy. It would have to be a spiral galaxy as nearly planar as possible, appearing from the Earth right on edge. The two images would then be beyond each arm. And the distance beyond each arm would be expected to be the same, since spirals are not lopsided either. This is how real lenses would work.The standard model of lensing wants us to believe that very imperfect lenses could focus light from that distance here upon the Earth. Two beams of light are focused, but each beam is bent a different amount. Anyone who knows anything about lenses knows that is highly unlikely. It was unlikely enough when the focusing was done by a centered and homogeneous lens or galaxy, but now that we see that the lens is lopsided and undefined, it destroys the theory in two separate ways. One, it requires us to believe that the two different bends focus perfectly here on Earth. Two, it requires us to believe that nearly homogeneous elliptical galaxies can bend two nearly parallel beams of light in very different amounts.
Concerning this last point, remember that the proposed distance between the quasar and the galaxy is 5 billion lightyears. Even if the quasar were larger than the largest galaxies, the beams of light would be nearly parallel at that distance. BUT, quasars are not thought to be that large, as a matter of diameter. They are called “quite compact,” since they are now proposed to be the center of a galaxy, surrounding the central black hole. Mathematically, then, the light emitted by the quasar would be parallel when it reached the lensing galaxy. How can an elliptical galaxy bend some of this light more than the other?
Then there is the amount of bending we are told we are seeing here. The beam from image B is bent about 1”, which, you will remember, is about the amount the Sun is said to bend starlight, relative to the Earth. How much is 1” at 3.7 billion lightyears? It is about 18 thousand lightyears. The light we see from the B image is passing 18 thousand lightyears from the edge of the lensing galaxy. So this galaxy is bending light 18,000 ly away as much as the Sun bends light right on its surface. That is pretty difficult to believe, since that galaxy, like every other, is made up of stars. Let us say we transported ourselves to a medium sized star on the edge of
YGKOW G1. Light from the quasar behind will be passing this medium-sized star, and the star will be bending it. How much? Well, if the star is about the same mass as our Sun, the light will be bent about 1.7”. So we have light right on the edge of the galaxy being bent 1.7” and light 18,000 lightyears away being bent 1”.Mainstream physicists will swallow hard and say, “No, we have to sum the mass of the galaxy. We can’t just pick a star and work from there. The galaxy has a huge mass, so even that far out you would expect a bend.” OK, let us assume that is true. If it is true, then the bend due to the galaxy should increase by the inverse square law as we get closer to the galactic edge. If the bend at 18,000 ly is 1”, then the bend at the edge of a large galaxy should be about double that. If we translate that finding to our own galaxy, then the bending of light in our solar system should be due at least as much to the galaxy as to the Sun. The Sun is at a great distance from the galactic core, so light in this region should be bent noticeably. Depending on where the galactic center was relative to the Sun and light, that center might either double the bending or negate it entirely.
While the standard model may or may not be able to contain that fact, it certainly cannot contain the next fact. If we look at the bending of image A of the Twin Quasar, we find more bending at a greater distance. The two images are about 6” apart, with the galaxy taking up about 1-2” of that spread. So image A is about 3-4” away from the edge of the galaxy. This means that the light is passing about 60,000 ly from the edge of the galaxy, and being bent at least 3”. And this means that we have greater bending at a greater distance! So any input from nearby globular clusters will not be a fractional correction. It will be a huge correction to a gravitational field that is not working at all like it should. Gravity normally decreases with distance.
In fact, the input from the globular cluster on that side must be greater than the input from the galaxy. Which means the globular cluster must have either a huge mass or a very close pass. And if that is the case, then we don’t really have a lens here. We have two coincidental bends from two separate objects creating the appearance of a lens.
Clearly, then, this twin quasar is a poor candidate for a lens, and we should be surprised that the standard model of lensing leads with it. I would say that the inverse square law is fatal to it, since we shouldn’t expect more bending at a greater distance.
Even more fatal to it is that this distance analysis reveals a peculiar outcome of gravitational bending. According to the theory, there should be a distance beyond every edge of every galaxy and every star where the light behind is bent just the right amount to reach us here on Earth. All objects that we can see have other objects behind them. Every star we see has stars and/or galaxies behind it, and many objects we see are eclipsing objects of considerable brightness. If bending and lensing were true, we would expect every single object in the sky to be fully haloed. No, more than that: we should expect the entire sky to be filled with bent light.
Every object we see has an object behind it or near it, and every object has a distance of bending beyond every edge where the angle would be right to bend the light to us. Therefore the night sky should be filled from corner to corner with multiple images. According to the theory of light bending, there shouldn’t be a dark dot in the sky.
We can see this just by looking again at the Twin Quasar. As the light from the quasar filters through all those galaxies in the cluster, as well as through the globular clusters between, it will be bent in an infinite number of ways. Each distance from each galaxy or cluster causes a different bend, which then gets rebent by the next galaxy or cluster. Before long the image should be completely randomized, so that we see not a quasar or two quasars, but a giant patch of diffuse light. There is simply no way to explain the fairly discrete images we see given the theory of bending.
You can see that astronomers have been unbelievably sloppy in their presentation of the Twin Quasar as a candidate for bending. They have put it forward as proof of General Relativity, when in fact it is proof of nothing. If anything, it is proof against the current interpretation of GR, and of curved space.

Einstein’s cross, another famous candidate, is equally weak. Here you can see four distinct images, all said to be the same quasar. But even on a first glance, you can see that the four images are not symmetrical. The lensing galaxy isn’t even between the top and bottom images. How can a lens work when it isn’t in the same line as the images we see? To create this set of images, the center of mass of the lensing galaxy would have to be outside the galaxy.
Just as strange is the fact that we have images that are roughly top, bottom, left, and right, but absolutely no signs of arcs or rings. Because we have images in four different directions, we would expect a fairly balanced lens. A galaxy that was fairly balanced in the four directions would have to be nearly spherical--or at least nearly circular in the plane we see--and this would mean the field must change gradually, as a curve. And this must mean that we would see arcing. Unless it is being proposed that this galaxy is a cube, or acts like a cube as a gravitational object, we cannot explain this set of four distinct images. To be balanced like this, with no arcing of the images, the galaxy would have to be nearly square in this plane. If the galaxy is elliptical or spherical, and balanced in these four directions, we would expect arcing. The gravitational field cannot be shaped in this way. You cannot explain the total loss of image in the four corners, much less the total lack of arcing along the circumference, near the images. All four images are crisp and unstretched along the circumference line, meaning the gravitational field is not acting like a curved field at all.
If you press for information on Einstein’s cross, you begin to get the truly absurd, as we find in this explanation from the University of Tennessee physics department:
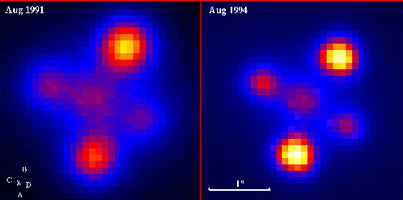
The important thing to notice here, though, is not the variation over time. Even more important is that this photo allows us to see what we only suspected with the small BW photo above: the four images are not the same brightness, even at the same time! They look vastly different. Even opposite images are not equal to each other. It would appear that the only thing these four images have in common is the redshift. But since we do not know the local velocities, we cannot say that all four are at the same distance. To get a distance from a redshift, we have to assume the object is moving locally due mainly to universal expansion, or to original Big Bang forces. If it is not, it could be at any distance.
Furthermore, if the given theory were about stars in the galaxy obstructing light from the images in different ways in different years, we would still have a problem, since the top and bottom images stay larger and the left and right images stay much smaller. Star obstruction would change fairly rapidly, and with such a mechanism we would expect the four images to average the same brightness over time. Their maximum brightnesses over time should also be about the same, since during some intervals each quasar would be expected to hit emptier patches in the galaxy. If the four images are of the same object, the images should average and maximize in similar ways. But that is not what we see from these photos.
These photos also confirm the absence of arcs. More than that, they show, if anything, a stretching of the four images radially, toward the center of the central galaxy! This is especially clear in the first image. How could bending or lensing compress an image along the circumference, or, to say the same thing, stretch it radially? Einstein’s Cross flagrantly contradicts the fundamental theory in many places.
It might be called folly to try to explain four unequal images as the result of lensing. When those images vary from year to year, it is even more foolish. When those images are stretched radially, the whole effort becomes a farce.
The Thunderbolts have also come out against the current interpretation of Einstein’s Cross:
Using the Hubble Space Telescope, a friend of Halton Arp documented that quasar D (right side of photo) is physically connected to the nucleus of the galaxy. Later, a high redshift connection was discovered between quasars A (bottom) and B (top) which passes in front of the connection between the nucleus and quasar D. But these observations went unnoticed: the journal which usually prints results from the Hubble Space Telescope rejected this announcement twice.Mathematical analysis, too, casts doubt on the gravitational lens theory. The faint foreground galaxy would need to be much bigger and brighter in order to accomplish this lensing feat: In fact, it would have to be 2 magnitudes brighter than "conventional quasars," the brightest objects known.4
While I am not agreeing with Arp that these four quasars have been ejected from this galaxy, I do think he and others have found many fatal flaws to the lensing hypothesis. Every time anyone takes a close look at the theory and at the offered examples, they discover that the numbers don’t add up.The truth is, the lensing hypothesis has no strong proof. It doesn’t even have circumstantial evidence that looks convincing, as I have shown. Prima facie, the hypothesis is weak, and the more one studies the examples, the weaker it gets. The theory is never defended in a cogent manner, it is simply asserted, and all anomalies are ignored. The Twin Quasar and Einstein’s Cross are not strong examples, but every page on gravitational lensing leads with them. This is itself a tip-off, for if stronger examples existed, we would not need to hear of the weak examples. Critiques, in the few instances they pop up, are also ignored or suppressed, as we have seen with Arp. This is how the standard model operates, on all questions. There is no possible defense of its nebulous hypotheses, so its only hope is to reject announcements and papers, to browbeat anyone who sits still for a moment, and to pre-empt discussion by a constant professional patter of propaganda.
As proof of this, we may go to the Physics Forums, where we find someone asking about Einstein’s Cross. A forum member says, “Is the lensing galaxy rectangular ? Why is the lensing effect producing four distinct images and not some distorted circular patterns?” The local expert, MrCaN, answers,
Its not a straight line: the quasar in the back is off a little bit, which creates the four points. Actually the light is bent spherically, but due to the alignment, it peaks at four points, and the other stuff gets lost in space. That is, it is so small it doesn't show up, and if you increase the exposure time, the galaxy in front will saturate the image.5
For some reason our forum member is satisfied with that terrible answer: members who argue with the experts are routinely shunned and then banned, so it is best not to make much noise. But let us look at the answer here. The light is bent spherically, but peaks at four points: that is not an explanation, that is a statement. “We see four points, therefore the image peaks at four points.” Zero content. Even if the image did peak at four points, for some physical reason not mentioned here, the image would not be expected to “unpeak” right at the top and bottom edge of the images we see. We don’t see “peaks,” we see spikes surrounded by zero amplitudes. In fact, a quasar “off a bit” from center would not create peaks, much less spikes. It would create a bent image on one side only, or at the most two sides. It could not create four images, since it would have to create unequal bending in order to do so. To make this even sillier, our expert says, “the other stuff gets lost in space.” The light in the four corners is so dim, it gets soaked up by the vacuum, I guess, by some mechanism of light destruction so fundamental it doesn’t have to be mentioned. Equally silly is the idea that “the galaxy in front will saturate the image.” The galaxy in front is not as bright as the quasars, but if we give it time, it will become brighter than them and fill up all the dark spots, relieving us of our need to look at them and ask questions about them.
I will be asked what does cause the multiple images? Is it my “wild” expansion theory again? No. Expansion can’t explain multiple images at that distance or any distance, since the appearance of bending is caused by the relative motion of the observer. An astronomer at a telescope can be moving in one direction only, so he cannot move into two separate beams simultaneously. He could see an object in the “wrong” place, but he could not see it in two wrong places.
I think the explanation for lensing is much simpler than any we have been presented with. In the case of the Twin Quasar, one of the images is probably real, and the other one is refracted. Something about 3” out from
YGKOW G1 is refracting light from the quasar, creating image A. All that is required is that one of these galaxies in the cluster, or one of the globular clusters, has a real halo of cast-off dust or gas capable of refracting the light beyond. If this halo is at the right angle relative to us, it will refract light to us.Of course, this would also explain the so-called Einstein rings of other “lenses,” without any need for lensing. Many galactic objects would cast off material in spheres or circles, causing circles of refracting material of the same sort. Since galaxies are normally well-centered, these rings would also be fairly homogeneous, having, for example, the same constitution and therefore the same refracting index.
As for Einstein’s cross, refraction is once again the most likely answer. Probably we had a real image and its refraction already existing before it reached this area of second refraction. Some field of gas well behind the galaxy we see created two parallel-running images. Other images from the quasar were then brought together by gas near this galaxy, creating four images. This would explain the distinct images as well as the lack of arcing or rings.
Both rings and distinct images can be explained by refraction, since matter can be cast off either in jets or in haloes. Haloes will give us arcs of refraction and jets will give us a distinct area of refraction. But lensing cannot explain the lack of arcing we see in Einstein’s cross, since galaxies cannot create square lenses.
So you can immediately see that we don’t need an esoteric explanation of bending, when we already have a prosaic explanation. Even before I showed the logical inconsistencies of the theory of lensing, it was much more likely and plausible that rings and arcs and multiple images were caused by refraction than by gravitational bending. Astronomers assigned the phenomena to gravity only because they were already in search of such “proofs.” They needed the bending to be caused by gravity, so they ignored the more likely explanations. As in so many other instances, they let the theory determine the data. Instead of having data, and then developing a theory to contain it, they had a theory, and then went in search of data to support it. The science of the hysteron proteron.
But now we can see that logic supports refraction, and refutes lensing. This is because refraction can explain the very limited instances of bending we do get. Refraction requires that we have an area of refracting medium, of the right refraction index, at the right distance, and at the right angle, in order to send an image to us. This would be expected to be a fairly rare occurrence, even at universal scales. It certainly would not be the standard experience of every image. But if the theory of gravitational bending were true, every single massive object in the sky would be bending light to us. Every visible and invisible object, including every star and every galaxy, would be bending light to us. Every object would be surrounded by literally thousands of haloes (of varying brightnesses), since every object behind it would have some angle of refraction at some distance from its edge, that would bend the light to us. We don’t see this, so we can’t be seeing gravitational bending.
1http://www.phy.ohiou.edu/~tss/ASTR410/Lancaster04/paper.html
2http://www.universetoday.com/2006/08/07/the-universe-could-be-larger-than-previously-thought/
3http://csep10.phys.utk.edu/astr162/lect/galaxies/lensing.html
4http://www.thunderbolts.info/tpod/2004/arch/040726nebula.htm
5http://www.physicsforums.com/showthread.php?t=1375
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.