go to homepage
Email me at mm@milesmathis.com
To read a more concise expression of my central arguments in this long paper,
click here to go to my 2001 submission to Annalen der Physik
An
Algebraic Correction
to
Special Relativity
by Miles Mathis
Abstract
First written November 1, 2000
Here at the very beginning I want to state clearly that in correcting the transformation equations of Special Relativity, I am not thereby exploding Relativity as a whole. I accept time dilation and length contraction. I accept the speed of light as a constant. My critique of Einstein's equations is an effort to fine tune them, not to jettison them.
I fully understand the current state of the conversation on Special Relativity. I know that SR has met fierce resistance from "classicists" and that the scientific status quo has been forced to take a rather extreme stance against those who seem to them unable to follow the concepts and math of the theory. However, I will show that the math is subtly flawed nonetheless, and that it must be corrected in order to make the equations continue to match experiments. In that sense, this paper is an effort to bolster the theory of Special Relativity, not to tear it down. If this paper proves anything, it proves that a return to pre-Einsteinian concepts cannot be preferred.
As an olive branch to the classicists, though, I must admit that the mathematical errors made by Einstein have been a large part of the problem in understanding his theory. It is no surprise, really, that it has remained impenetrable to many intelligent people. My conversations within the scientific status quo have shown me that none of them understood it either. They simply had access to raw data that confirmed the theory, and that was (understandably) good enough for them. Only now that we have reached a level of precision where experiments are no longer confirming SR is there an opportunity to look again at the equations objectively, without all the name-calling and high emotion.
So, I repeat, this paper is not a philosophical or metaphysical treatise. It is not an attempt to discredit Einstein or Special Relativity. It is not the call for a return to Newtonian physics. Nor is it the proposal of any supraluminal or trans-Einsteinian theory. It is the discovery of the actual mathematical errors in Special Relativity. I follow Einstein line by line and show precisely where the mistakes are. In this, I believe I may be the first. The most notorious critic of Einstein, Herbert Dingle, said (Nature, 1967) "I have enough mathematical insight to see that it is a waste of time to look for mathematical flaws in the theory." Few, if any, have bothered to look at the basic math in the years since, believing the equations to have been already combed by the best minds of the century and proved beyond a reasonable doubt by field tests. But in the last decade, field tests have put the equations into question again. Despite this, nearly all (if not all) of the mathematical and theoretical work has gone into making these new tests fit the equations, rather than vice versa. This paper shows that the fault lies in the transformation equations and that they are easily correctable.
Specifically, this paper was written in response to the call by the Jet Propulsion Lab for help in understanding why the equations of Relativity were yielding wrong numbers in their calculations on space satellites (the so-called Pioneer anomaly). To date, no explanation has been offered for the discrepancies, despite many replies to the call for help and many theories published in Physical Review Letters and elsewhere. My paper is unique in that it offers new transformation equations, with which I make predictions about the numbers generated by JPL. That is, I have solved a concrete problem of applied mathematics, and I have the numbers to prove it.
I first discovered the central tenets of this paper in November of 2000. The bulk of the paper was written before Thanksgiving of 2000, and it was in final form before the end of that year.
What follows is the paper almost exactly as it was presented to PRL in early 2001.
Table of Contents
Abstract
Introduction
Part I: The Equation x' = x - vt
Part II: The Equation x = ct
Part III: Lorentz, Michelson and Pythagoras
Part IV: New Transformation Equations
Part V: Relative Velocity of an Approaching Object
Part VI: Relative Motion at an Angle
Part VII: The Addition of Velocities (two degrees of Relativity)
Part VIII: Conclusion
Part IX: Inferences (Including the Twin Paradox, Hafele Keating, etc.)
Part X: A Prediction (Concerning the Pioneer Anomaly)
Appendix A: The Michelson Morley Interferometer
Appendix B: The L and t Transforms
Appendix C: Einstein's 1905 text (from Annalen der Physik): a line for line analysis of the original math.
In this paper I will show that the first equation of Special Relativity, the famous x' = x - vt, is not applicable to the problem, since it is not Newton's "Principle of Relativity," nor a "Galilei transformation." I will do this with simple algebra. Introduction to the Problem Only very recently has there begun to be a general acceptance by the status quo that Special Relativity might be subtly flawed in some way. For most of the 20th century, of course, it was sacrosanct. No one in the mainstream would have thought to question it in any way. But now there is beginning to be an accumulation of data that does not fit Einstein's transformation equations precisely. The data that led me to work seriously on the problem was supplied by the Jet Propulsion Lab. For several decades, various space satellites have been found to be acting a bit strangely. They are not where they are predicted to be according to relativistic calculations. The scientists who manage these craft have dismissed any number of explanations for the discrepancy, supplied to them by many of the best technicians in the field. But still the problem is unresolved. It has proven to be such a thorn that the JPL has even gone to the mainstream publications in the United States, begging for help. Newsweek published a major article on it in 1999. Part I: The Equation x' = x - vt This illustration is very much like Einstein's train illustration in the book Relativity, but here the artist has tried to graph x', x, and vt. The man is at point P: meaning that x' is the x-distance from the origin to P, in S'. We, the observers, are understood to be watching from the embankment in S, the co-ordinate system to the left Part II: The Equation x = ct ~~~~~~~~ Some physicists may now be shaking their heads, saying to themselves, "no, no, no." They will tell me that Einstein's first equation describes a completely different situation than the one I have plotted and critiqued above. They will say that the equation x' = x - vt breaks down in a wholly different way. ~~~~~~~~ ~~~~~~~~ Part III: Lorentz, Michelson, and Pythagoras Part IV: New Transformation Equations to read the rest of the paper click here
I will then show that the equation x = ct is also not applicable, since it implies that length contraction and time dilation are mathematically in direct proportion, when they are in fact in inverse proportion. I will also show why Einstein's equations are so nearly correct, despite being arrived at by faulty math.
Next, I will correct these errors and offer new transformation equations. These new equations will be arrived at in a straightforward way, again with simple algebra. Furthermore, I will show that Einstein's transformation equation for velocity is an equation for two degrees of relativity. I will show that there exists a velocity of one degree of relativity, and I will provide a transformation equation for it.
I will then derive the corrected transformation equation for two degrees of relativity, for velocity.
Next, I will solve the specific problem of the Jet Propulsion Lab, making a prediction for the exact amount of error in Special Relativity that leads to the faulty numbers in General Relativity.
Next, I will show that the present interpretation of Special Relativity—as applying equally to objects in all relative trajectories—is in direct conflict with other currently accepted facts, including Roemer's calculations on Jupiter's moon Io and data from the binary pulsar PSR 1913+16 (and all other pulsars and multiple stars). I will show the simple and inevitable resolution of this conflict.
Next I will prove that Lorentz made the same error as Einstein, and that this error was caused by a faulty interpretation of the Michelson-Morley interferometer. I will show that the diagram used to visualize the interferometer by Lorentz, Michelson, and every physics textbook in the 20th century is conceptually flawed. And I will show precisely where this flaw lies, mathematically, and how it led to the equations of Special Relativity—especially the Pythagorean component of gamma.
Finally, I will interpret the new equations, showing how they must change our conception of the nature of Relativity, of light, and of the operation of measurement itself.
Einstein published his paper on Special Relativity in Annalen der Physik in 1905. The book Relativity was published for general audiences in 1916. This book and other books on Special Relativity published by Einstein have gone through many editions, but the theory itself has not changed in the last 96 years. Einstein made several predictions which were confirmed by subsequent data, and the theory quickly achieved a solidity and a fame that is unmatched in history.
His intention was to reformulate Newton's equations for velocity to conform to the latest facts. Light had recently been shown to have a finite and constant speed, and Einstein saw that this would affect calculations of position and velocity of measured objects. He saw that the measurement of time would be likewise affected. Lorentz had already offered a transformation equation for length, but Einstein provided a theory to contain Lorentz's ad hoc math. And Einstein also went beyond Lorentz in providing equations for time and velocity.
Maxwell was the first to propose that moving fields altered the dimensions within them. Poincare offered theoretical justification for this, and influenced both Lorentz and Einstein. To prove Maxwell's hypothesis, Michelson set up experiments in 1881 and again in 1887. By these experiments, light was shown to have a constant speed regardless of the speed of the observer. The second experiment included the famous Michelson-Morley interferometer. The interferometer (which is diagrammed in this paper) was designed to show the velocity of the earth relative to the "ether." It was assumed that light traveled either through, or relative to, this ether; and that therefore the velocity of the earth would have to be added or subtracted from the velocity of light. But the interferometer found that the earth's velocity had no affect upon the measurement of the speed of light from any direction. This was one of the most mysterious outcomes in the history of science. In trying to explain this null set, Lorentz proposed a set of contractions and expansions that would offset the predicted measurements, bringing them into line with actual data. His fudge-factor turned out to be a now-famous term called gamma.
Not accidentally, Einstein's basic transformation term is also gamma. Einstein was working independently of Lorentz and on a different problem, but they both used the same concepts and the same math and so came to the same term.
Einstein began his derivation by postulating two co-ordinate systems, S and S'. S is the co-ordinate system of the observer. S' is the observed co-ordinate system. He then provides us with the basic equation x' = x - vt, which he tells us is the Galilean transformation equation from one system to the other. This also gave him x = x' + vt, he assumed. He then produced the equations x = ct and x' = ct' to show the distance light travels in the two coordinate systems. He introduced gamma as the transformation term, as in the equation x' = γ(x - vt) where γ is gamma. By substituting values among these four equations, he achieved a value for γ in terms of his other variables.
Quite simple, really. Except that he never precisely defined his terms. Not in the original paper. Not in the book. Not ever. And no one has ever questioned these terms
The mysteries of Special Relativity have been considered up to now to be inherent in the problem. We have been told that it is not comprehensible by ordinary mortals. It is subtle and complex, and all one can do is accept the paradoxes. That is all part of the fun, frankly. If it were transparent, it wouldn't be deep. This is the current wisdom, anyway.
Unfortunately, it turns out that the confusion is Einstein's (and Lorentz's and Michelson's, etc.) from the beginning. It is possible to define the terms precisely enough that all the mystery disappears. We are then left with distressingly simple equations that almost anyone can understand.
Over the last century there have been any number of lengthy critiques of Special Relativity. The bulk of these have been philosophical rather than mathematical, however. The argument about Special Relativity has split into two distinct factions. On one side is the vast majority of physicists who accept SR, due to its experimental success. On the other side are a minority who feel that time dilation makes no logical sense. Their theories therefore revert back to pre-Einsteinian physics, where things are tidier. It turns out they are both wrong. Special Relativity is conceptually correct, in most ways. The experimental success of Einstein is no accident. Therefore the physicists who treat nay-sayers as "cranks" are correct, in the majority of cases. A return to Newtonian mechanics would be a step backward. However, Einstein did make some conceptual and mathematical errors which have never been corrected. Some of these are absurdly simple algebraic mistakes, which tend to vindicate the so-called "cranks" who believe that famous physicists don't comprehend the theory themselves. In the early part of the century, physicists could admit this uncertainty, for the most part. Einstein himself admitted some confusion about SR up to the end. Karl Popper asked him a straightforward question about the Twin Paradox in the late '40's. He had no answer, and said so. Bohr said that only six people understood the theory, but we are not sure he meant he was one of the six. If he had fully understood it, he would have corrected it.
Until now no one has yet been able to point to the specific errors in the mathematics. Admittedly, Einstein's explanations made this quite difficult to do. And the spectacular successes of the theory acted as a sort of protective wall, keeping it from being seriously questioned. Institutions like the Jet Propulsion Lab could not publicly (or even privately) question such a fortified theory, without direct mathematical evidence. I only hope the following paper will begin the thaw.
Einstein begins his book Relativity with a famous thought experiment.* It involves a railway embankment, a train, and a man on the train. The train moves with a constant velocity v. Later, the man also moves, with regard to the train. But for now we will limit ourselves to the train and the embankment.
Let us start with an illustration.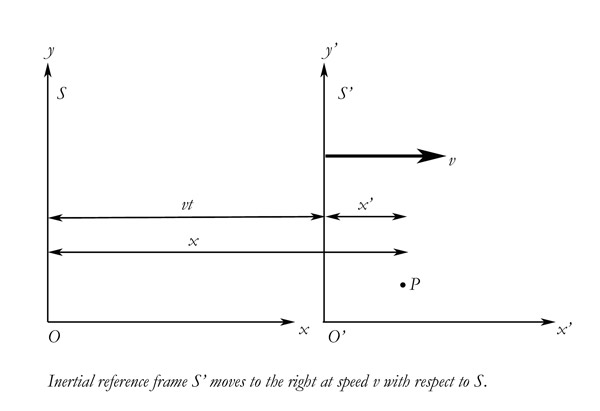
In the first part of the problem, the man is not moving inside the train: x’ is simply the distance of the man from the origin at t0. We are transforming the distance, not the velocity. We transform the velocity variable later, when the man also moves inside the train. Einstein makes this very clear in the paper of 1905, and it is obvious regardless. There is only one velocity variable given. If the man were moving relative to the train, we would have to be given that velocity as well, as you can see.
To go with this thought experiment, Einstein gives us this equation (p.33, Rel.),
x' = x - vt
In his original paper of 1905 [On the Thermodynamics of Moving Bodies], he gives the same equation. But neither there nor in the book Relativity does he say where this equation comes from. In the 1905 paper, the equation is completely mysterious; but in Relativity he gives us a clue. Einstein says, "If in the place of law of the transmission of light we had taken as our basis the tacit assumptions of the older mechanics as to the absolute nature of times and lengths, then instead of the above we should have obtained the following equations:
x’ = x - vt
y’ = y
z’ = z
t’ = t
"This system of equations is often termed the 'Galilei transformation.' The Galilei transformation can be obtained from the Lorentz transformation by substituting an infinitely large value for the velocity of light c in the latter transformation."
But this is not the case. There is no such thing as a Galilei transformation equation. For Galileo and Newton, no transformation was necessary for a linear problem like this. x in S' would equal x in S. Besides, the whole universe was a single co-ordinate system for Galileo, and the train would not have been given a system of its own. There is no possibility of a prime variable of this sort in a Galilei system. The only time that two Galilei systems would have two x variables is in a case where the two systems have different origins. The equation in that case would be something like x’ = x – a, where a is the distance between the two origins. In Einstein’s thought problem the origins are overlapping at t0. This is one of the givens. In the paper of 1905 he states outright that the origins are equal at t0. He is not trying to calculate the distance from one system to another, he is trying to export a distance in one system to another system.
*In the body of this paper I limit my critique to Einstein's explanation in his book Relativity, and the further elucidation of that explanation in other later books. Einstein changed the math of Special Relativity several times--and not just to simplify it for general audiences. The math in his original paper of 1905 contains many more errors than the later math, as I show in Appendix C. Critiquing all of Einstein's mistakes in SR, in all his various papers, would have unnecessarily lengthened this paper, and made it all but impossible to read. But those who are not convinced by my arguments here, or who believe that my math is too simple, are recommended to the Appendix.
This being so, the equation x’ = x - vt cannot be applicable to the problem. For you can see that the true list of Galilei transformations are these.
x’ = x
y’ = y
z’ = z
t’ = t
The velocity has absolutely nothing to do with a Galilei transformation. If c is infinite, then all measurers will measure equal times, distances and velocities. x’ = x, v’ = v. This is because there is no difference between what I see and what the train sees. Light brings me exactly the same information that it brings the train, at exactly the same time. There can be no transformation equation: not a fancy Lorentz transformation, but also not a simple transformation like x’ = x - vt .
Einstein has used the wrong first equation. He has imported a Galilei transformation that is true for points on two stationary graphs and applied it to points on two graphs moving relative to eachother. He assumes that the distance a between the origins after t will be vt, and that this distance will be added to x’, but this is not true. For one thing, the origin of S’ is not moving. If the origins were together at t0, then they are still together, since origins don’t move, by definition. This is just to say that if the train started from the station at t0, then after time t the train still started from the station, which has not moved. Train stations do not move, just as origins don’t move: t0’ and x0’ are still back at the origin, which is still back at the train station. The illustration above, which is exactly like every other illustration I have seen, is highly misleading.
Einstein is mistaking the back end of the caboose for the origin. Look at what the equation is telling us. Let’s say at t0 the back end of the caboose is at the origin of the moving system, S’. Let’s also say that x’ is the distance to the front of the same caboose, as measured from inside the caboose. The whole train then leaves us at the station and travels a distance given by the term vt. The equation x = x’ + vt is telling us that we, back at the station, will measure the length of the caboose as "how long the caboose is, measured from the caboose" + "the distance it has gone". As if we will add the length of the traintracks to the length of the caboose! Do you see now how utterly absurd this is? It assumes that we can’t see, with our own eyes, that the back of the caboose has also traveled vt, and must therefore be subtracted from x’ + vt. What we are looking for in this problem is simply "how long the caboose looks to us." This equation tells us nothing about that at all, not classically, not relativistically, nothing. It is the wrong equation. Classically, the correct equation is just x’ = x. Einstein imported an equation that Galileo would have used to find the total distance from the origin to the front of the caboose after time t, and applied it to find the length of the caboose as seen from the origin. An absolutely momentous blunder.
Some will say, "I agree with this last part, about the caboose, but it seems to me that the origin of S' does move. It is the same as the back end of the caboose." It is the same only if you assume that the train is not measuring its own velocity, too. If the train has no windows, and is not an active part of the experiment, then you can make the case that the back end of the caboose is the origin of S'. But as soon as the train starts measuring its own velocity, it must look out the window to achieve a background. Once it does this, its origin reverts back to the train station. If the origin of the train is the back of the train, then the train can never measure a velocity, from its own point of view. But it can, and must, for transformation equations to be found. It can, since any measurements are equally valid. It must, because transformation equations must transform something. If the train doesn't make any velocity measurements, then there is no velocity to transform.
To sum up, if light has an infinite speed, then the embankment will see both ends of any rod at the same time. The embankment will also see the back of the train and any other point on the train at the same time. So Einstein's given equation cannot be a Galilei transformation, in any sense. This mistake has never been corrected (I just saw the very same equation used by Richard Feynman to prove Special Relativity in Six Not-so-Easy Pieces—92 years after Einstein). Physics textbooks still use Einstein’s series of conceptual steps to prove the equations of Special Relativity.
This is the current derivation in physics textbooks:
Assume x' = x - vt
Assume that the transformation from Galilean equations to Relativistic equations will be linear. Then
Step 1: x' = γ(x - vt) where γ is the transformation term we seek.
and x = γ(x' + vt')*
Now, says Einstein (following Lorentz), light travels in these coordinate systems (S and S') in this way:
Step 2: x = ct and x' = ct'
Substituting the first equations into these equations gives us:
Step 3: ct = γ(ct' + vt') = γ(c + v)t' and
ct' = γ(ct - vt) = γ(c - v)t
If we substitute t' from the second equation into the first, we find that
Step 4: ct = γ(c + v)γ(c - v)(t/c) = γ2(c2 - v2)(t/c)
Cancel out the t on each side and solve for y:
Step 5: γ = 1/√[1 - (v2/c2)]
This is the famous transformation term gamma. But since the initial equations are not valid, the final equation is compromised. That is, gamma is false. This proof is false.
*Einstein used the equation x = γ (x’ + vt)—without the t primed. But current physics textbooks have changed the notation in order to make gamma derivable with an internally consistent series of steps, as above. The math is correct; the postulates and givens aren’t.
This leads us to the second major problem. Everyone knows that Einstein used the Lorentz equations to find that time appeared to slow down and x appeared to get shorter. Length contraction and time dilation. But let's look for a moment at the two light equations above. The light equations Lorentz and Einstein both used:
x = ct
x’ = ct’
If these are true,
then c = x/t from the first of these equations
and x' = xt'/t by substitution
so x'/x = t'/t
This means that in these equations the apparent change in x is proportional to the apparent change in t.
But when time slows down (in any system, or by any means of measurement), the period gets larger. Time slowing down implies a larger t, not a smaller t.
That is, t should appear to get larger as x appears to get smaller. Einstein even states this outright, in the book Relativity. He says (Ch.XII, p. 37) "As judged from K, the clock is moving with the velocity v ; as judged from this reference body, the time which elapses between two strokes of the clock is not one second but [γ] seconds, i.e. a somewhat larger time. As a consequence, the clock goes more slowly than when at rest." Again, he says "a somewhat larger time." Physicists have focused on the sentence after that, up to now. But time is not defined by the rate of the clock, not even by Einstein. Or stated more precisely, time is not measured that way. Relativity is primarily a theory of measurement, and so what is required is an operational definition of time. Not what time is as an abstract concept, but what time is as a measured quantity. Time is the length of the period, as Einstein flatly states here. A second is not a stroke of the clock. A second is the gap between strokes. Time is not the strokes of the clock, it is the time between strokes of the clock. As he says, a moving clock is seen by a stationary observer to have a period γt, which is larger than t. A dilated clock ticks slower because its period is longer.
[To consider this question further, see the links at the end of the paper—a discussion of this definition with several scientists and mathematicians, and a paper on the operational definition of time.]
As further proof of this very important concept, I refer you to the The Meaning of Relativity again. In Chapter 2 he provides this equation (eq. 22a):
Σ Δx’v2 – c2Δt’2 = 0
Conceptually this is obviously analogous to the equation x’ = ct’. Einstein is just varying his math a bit, dressing it up. The thing to notice here is the delta t. He has now made it clear that he is referring to changes in time, not instants in time. In these equations, the variable refers to the time period, not the instant in time. Which is precisely my point. When time slows down the period gets larger.
This being true, x and t must be in inverse proportion!
So, we should find that
x/x' = t'/t t = t'x'/x x = x't'/t
or xt = x't'
And, if x' = ct'
then c = xt/t'/t'
and x = ct' 2/t
Only if t = t' does t2/t' = t'
Einstein states that t does not equal t'
therefore x does not equal ct
Even the light equations were wrong!
Those with a knowledge of Special Relativity will interrupt here to point out that the transformation equation for x is only used to generate a length contraction equation, in the form
L' = L[(1 - v2/c2)1/2]
At least this equation is in a sensible form. But I must point out that length contraction along the x-axis implies a contraction of the entire x-axis. Which is a contraction of distance. Which should have been given us by the equation for x. [To get to the L equation from the x equation requires more sleight of hand, which I pick apart in Appendix B, if you are interested. Suffice it to say here that the x equation is not used by scientists, since none of them can say how it might be used.]
I also must point out that relativistic equations are used on quanta, which have no "length." And yet distance projections are made, such as the distance a particle will travel before breaking up.
And the satellites of the Jet Propulsion Lab are slowing down in ways that are subtly unpredictable by Relativity. This is obviously a problem of distance, not of length. Nobody at JPL cares whether the satellites are getting shorter. They care whether the total distance traveled is getting shorter. So the transformation equations are being misused, simply in order to make them work at all.
The equation may be thought of in this way, they will say:
Since, in general, x = vt, x' = x - vt may be thought of as
(some x) = (some x) - (some x)
It corresponds to the equation in the book that Einstein offers:
w = c - v
where w is the velocity of a light ray relative to the train,
c is the speed of light as measured from the embankment,
and v is the speed of the train
In fact, Einstein implies an analogy between the two equations. Therefore we may think of the first "some x" as taking the place of w.
Therefore x' is the displacement of the man relative to the train,
vt is the displacement of the train relative to the embankment,
so x must be the displacement of the man relative to the embankment.
I say, this makes perfect sense except for one very important thing. The notation of the variables is imprecise and confusing. x and vt appear (because of the fact that they are both unprimed) to be in the same co-ordinate system. But they are not. A much better notation would be the following:
x" = x - v't'
This tells us that we have three co-ordinate systems—the system of the embankment, the train, and the man. And this notation stands to remind us that the given velocity is v' : the local velocity of the train. It is the velocity of the train as measured from the train, not as measured from the embankment. Einstein never differentiates between the two. He never gives us an equation to find the velocity of the train as measured from the embankment—which would be simply v. The v he derives in Chapter XIII (on Fizeau) is the velocity of a moving man on the train, but it is for two degrees of relativity. He gives us no equation (and we still have no equation) for a single degree of relativity—the relative velocity of the train.
You may say, simply set the velocity of the man to zero and run the equation. This will give the velocity of the train. But it won't, for several reasons. One, because the current Lorentz equation for velocity resolves to unity if you plug in zero for one of the given v's. It tells you that your relative velocity is equal to your given velocity—the local velocity of the train. This is no surprise, since Einstein never differentiated between the two. This becomes crystal clear if you set x" to zero in the last equation above. The equation then becomes x = v't'. This tells us nothing. It also does not give us an equation that can be manipulated by substitution in the way Einstein manipulated his equation. What I mean is, x = v't' cannot yield the term gamma.
[Subsection added 10/2009] Professional physicists have ignored the above analysis, telling me that SR is known to be symmetrical, by Einstein's first postulate: "The laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good." That is Einstein's wording of it from the 1905 paper. These physicists tell me that the starting velocity is symmetrical, which is why we have no v'. If I measure your velocity as v, you will measure mine as v. That is true. Under that physical transform, velocity is symmetrical. But you must see that the equations of Special Relativity are not written for that specific transform. SR is not transforming your measurement of me to my measurement of you. In fact, if it were, we would need no transforms at all. If SR were really symmetrical in this way, we would need no t' or x' either. The actual transformational equations of SR are transforming local measurements into measurements at a distance, and there is no symmetry between those operations of measurement.
Yes, Einstein's postulate 1 is correct, if it is read correctly. The mechanical laws are valid in all frames, and you can take any frame you like as being at rest. In this sense, the laws are symmetrical. But if the operation of measurement is not symmetrical between these systems, then the transforms cannot be symmetrical either. That is, the laws are always symmetrical, but the “equations of mechanics” are symmetrical only when the physical operations between the systems are analogous. In transforming length and time in one system to another, the operations are not analogous. In Einstein's transformations, we choose quite freely to measure from one system or the other. Once we do, the symmetry is broken, because the measured system is not measuring us back. The transform is between “local numbers” and “measured-at-a-distance numbers.” There is no symmetry between those numbers.
This means that although Einstein's postulate 1 is still correct and valid, the velocity is not symmetrical across the transforms. Yes, there is a symmetry between “you measure my velocity” and “I measure your velocity”, but you are not measuring my velocity in the transforms. You are also not measuring my time or length or distance traveled. All the measuring is going in one direction only. For this reason, we do have two velocities from the start, v and v', and they are not the same number.
So far I have only done a critique of the algebra of Special Relativity. But the math more commonly used in Special Relativity is calculus. It has taken this form:
Let us say the man at point P in the illustration above is moving. The velocity of the man as seen from the embankment is therefore
W = dx/dt = d[γ(x' + vt')]/dt' where γ is gamma
Differentiation yields the equation
W = v' + v
1 + vv'/c2
But the form of this differentiation assumes that W = v' + v
where v' = the velocity of the man relative to the train, and
v = the velocity of the train
If v' = 0, then the equation resolves to W = v. v is a given quantity, so the equation yields no information.
Einstein's equation for velocity tells us how fast the man appears to us to be moving, if the man is moving in the train. But if the man is not moving with regard to the train, the equation tells us nothing about the apparent velocity of the both the train and the man relative to the embankment. No one has seemed to notice that the train has a relative velocity of its own. Or, if you take the given v as the velocity of the train as seen from the embankment, then no one has noticed that the train will have a local velocity that is different from this observed velocity.
Look again at the beginning of this calculus problem as I have stated it here. I have stated it as Einstein and the current textbooks state it: "Let us say that the man... is moving." Notice that there is no distinction in this sentence between 1) the man moving because he is moving with regard to the train, or 2) the man moving simply because he is seated in the train, and the train is moving.
By differentiating an equation of this form, Einstein has arrived at a velocity that is in fact relative to two degrees. That is, the man relative to the train, and the train relative to the embankment. The current transformation equations do not derive a value for the relative velocity of the train. Einstein and all the physicists of the 20th century have not even noticed that this value is necessary—that it is, in fact, the value we were seeking in the first place. Nor have they noticed that physics has ended up conflating, or substituting, one value for the other. This confusion of terms has never even been noticed, much less resolved.
In glossing the calculus of Special Relativity in the section above, I said that Einstein's equation for velocity gives us a number as long as the man is moving with regard to the train. What I did not say is that it gives the wrong number for that as well. It is wrong not only for the substitution and conceptual mistakes I have already outlined, but also for the following reason.
The main feature of the Lorentz equations is the term γ. As I said above, Lorentz and Einstein calculated gamma to be
γ = 1/√[1 - (v2/c2)]
Where did they get this? Lorentz arrrived at gamma first, and his thinking was not precisely the thinking of the substitution equations I have listed the steps for above. It is obvious from its form that gamma comes from applying the Pythagorean theorem to something. But what? Lorentz intially came up with his equations to answer the findings of the Michelson-Morley interferometer experiment. This was before Einstein proposed the theory of Special Relativity. I break down the interferometer experiment in chapter 3, but a simpified illustration here will show where the Pythagorean theorem comes from. This illustration was modified from a current college physics textbook.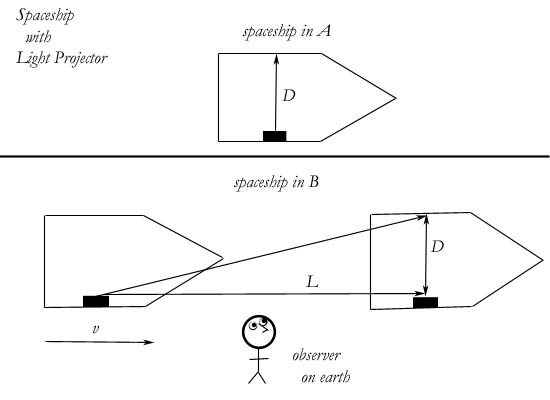
We have already seen two algebraic errors by Einstein in the invention and derivation of the Lorentz equations. The third—Lorentz' use of the Pythagorean theorem in deriving his original equations—arises from the problem illustrated above.
What we find in the illustration is a spaceship with a light projector inside. The projector emits a ray of light and it travels across the spaceship to a screen on the far side. The spaceship at the top is the S' system, and it illustrates the path of the lightray as seen from inside the spaceship (A). Below is illustrated how the path of the lightray would look from the outside (B), to a stationary observer on the earth. This is the S system, obviously.
We are told that the observer on earth would observe the process in B as it is illustrated. But notice that in B the lightray is moving sideways to the observer on earth. I hope is is obvious that our observer cannot see this lightray. No one can see a tangential lightray! We only see lightrays that come into our eyes. Every lightray we see is coming directly toward us. We have no knowledge of lightrays moving away from us or moving tangentially or even just missing us. To have information about the situation on this spaceship, we must be sent a signal from the ship directly toward us. In this illustration, the editors of the book are performing equations on imaginary light paths. Not observed paths, but abstractions. This is a grievous conceptual error.
To state it another way, in the A part of the illustration, measurements are being made by observation. In the B part, measurements are being made by the imagination. In A the local observer is collecting real data. If you had a person or device with the projector to collect the light rays as they returned from the screen, you could use this data to do calculations. But in B the observer is not basing his equations on collected data. He is not even collecting any data. There are no lightrays coming to him, and he can have no direct data concerning the motion of the given light, or indeed the motion of the spaceship itself. In reality he would not be seeing anything. The spaceship would pass him by, unknown. He is making assumptions. He is assuming that if he could see the same lightray A sees, it would be traveling in this manner. But this is not observation, much less measurement. It is poor illustrating, poor thinking, and very poor applied math.
The Michelson-Morley interferometer was invented to to test the situation described above. You can see how the Pythagorean theorem would be used to calculate the distance light travelled in B given the distances D and L. D and L are the sides of the triangle and the path of the lightray in B is the hypotenuse. The Lorentz equations applied to the interferometer work in exactly the same way. The Lorentz transformations take us mathematically from A to B.
This would be fine if the light ray appeared from the earth to travel that path or that distance. But, as I said, the little man does not observe that hypotenuse. It absolutely cannot be part of his data!
One of the outcomes of Einstein's relativity is that all events are local. That is, all measurements (of time, distance, etc.) are good only for the measurer. Another measurer in another place will get different measurements. And yet, by applying the Pythagorean theorem to this situation, the inventors of the visualization are attempting a non-local measurement. They are taking information obtained in a local field [specifically, the distance D, obtained by local measurement in A] and transferring it into a non-local reference field [the field in B]. This is not allowed, by the very theory they are trying to prove. In this way, the argument is circular. In order to prove that all events are local, and that time and distance are relative, they assume that quantities can be transferred from one system to another, and that D and L in A are the same as D and L in B. But quantities like D are transferable only if t and x are equivalent in both fields. Besides, D is a local measurement of the co-ordinate system A, while L is an observed distance in B, and yet they are treated exactly the same. No transformation equations are done on either one before they are plugged into the same right triangle!
I say "they," but it is not just the authors of textbooks who use these illustrations or the artists who create them who are to blame. Lorentz and Einstein do the same thing. Every illustration or conceptual analysis of this problem I have ever seen makes this same error. The Lorentz equations came from precisely this sort of diagram or visualization, and the Michelson-Morley experiment accepts it as a given. It is the very reason that the Lorentz equations have the form they do. If the equivalent of this diagram had not been the accepted view at the time of the Michelson-Morley experiment, the Lorentz equations would not have had the form of the Pythagorean theorem. As I will show, the true equations for simple time dilation have no Pythagorean component at all. [The equation for an object moving at an angle to an observer will use plane triangle trigonometry, but not the Pythagorean theorem].*
*To read more about Michelson-Morley, or to see a diagram of the interferometer—and see its equivalence to the diagram above—see chapter 3.
The analysis above also applies to the most current visualization of time dilation, which is the “light clock”. This visualization is now included in most up-to-date explanations, since it appears to give the shortest road to the first equation for time. You can see that the diagram below of the light clock is the same in most respects to the last diagram above. It is just a close-up view of the projector inside the spaceship, except that now the projector is made into a clock. We again use the Pythagorean theorem to find the third leg of a right triangle, and this equation yields the dilated time.
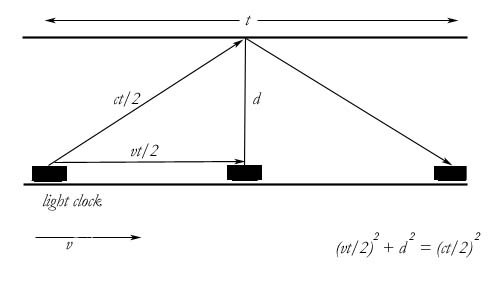
But the diagram again provides a false visualization. A light clock works by emitting a light ray. This ray reflects from a mirror opposite the clock and returns. One round-trip of the light is a tick of the clock. The diagram is meant to be a visualization of what a distant observer would see. This distant observer sees the clock moving at velocity v. The diagram must be from the point of view of a distant observer, since a local observer would not see the clock moving. The clock itself could not possibly see itself moving, since it has no velocity relative to itself. But the creator of the diagram assumes the distant observer would see light moving as it is diagrammed. In fact, he would not. A distant observer would not see the light at all. The light is moving perpendicular to his line of sight, and is invisible by definition. The vector ct/2 is imaginary. It cannot be anyone’s data. It is an assumption, and it is a false assumption. The light does not travel in that way.
Light always travels in the local field. In the final analysis, this is simply because the local field is real and the observed field is not. A field observed from a distance is a transform field, or a mathematical field, or an optical-illusion field. It is only apparent. The vectors within this apparent field exist only in the math. They do not exist physically. Therefore there is no way that light can physically travel along these vectors that are diagrammed. Light travels straight over and straight back, and neither the light nor the clock are concerned with how that looks to us from a distance.
It is true that the time will be dilated for the distant observer, but not for the mathematical reason diagrammed here. The time will be dilated due to differences in the signals the clock sends to us directly. To know what is going on with this light clock, the light clock must send us information in some way. Most of the time this information will arrive on light rays, whether it is visual or not. It is these light rays that actually come to us that we must do the transforms with.
In the light clock diagram, the creator of the diagram has shown us three separate positions of the clock. If we assume that the third position is farther away from us—as distant observers—than the first position, then it must take light longer to reach us from that third position. This, by itself, will create time dilation, since the period of the clock will be stretched out.
The transforms of Relativity must be done on light rays that are part of our data. We cannot do transforms on imaginary light rays. Special Relativity applies to real data, to real observations, and cannot be applied to non-verifiable assumptions or imaginary vectors.
As further proof of this, let us analyze the diagram with a bit more rigor. Notice that the clock in the first position needs to send the light ray off at an angle. How does the clock know at which angle to emit the light? You will say that we are using light that is emitted in all directions, so that some of that light will reach the clock at the third position. But what if we imagined a light clock that did not emit light in all directions. What if we assume a light clock that sends out a laser? Does the creator of this diagram mean to imply that if our clock sends out a laserbeam straight across to the far mirror, it will come back and miss the clock, since the clock will have moved on? Unlikely.
You may answer that the laserbeam emitted from the clock will act like a ball bounced by a boy on a bicycle. If a boy bounces a ball while riding a moving bicycle, the ball comes back to his hand. This is because the ball has a forward motion as well as a bouncing motion. If you answer this or assume this, you have broken Einstein’s Postulate 2. To paraphrase: “The speed of the light is independent of the motion of the source or the receiver.” The laser is emitted at speed c at one and only one angle. It cannot also have a forward motion. This forward motion would be a forward velocity, which would take its total velocity above c.
You may now answer, “OK, so the diagram has problems. But you yourself admit that the laserbeam will end up at the third position. How else can you diagram it?” The answer is: you cannot diagram it properly. It is impossible to diagram three separate events on one piece of paper. The false light vector is caused by trying to compress three events into one diagram. You end up getting a pretty good idea of how the sequence of events might unfold relative to a distant observer, but you get a very skewed idea of the way that light is traveling. This is because the light traveling is not an “event” to the distance observer. As I keep saying, that vector is invisible: it is not a possible part of his data. That vector exists only in a diagram like this, which is a compressed and false diagram. The real event is not taking place at a distance. The event of light traveling across to the mirror and back is a strictly local event. Light can be seen only where it is. It cannot be seen where it is not. Light cannot be seen at a distance. Therefore you cannot transform the light itself. You can only use the data given you by light to transform other things.
Einstein himself admitted this, and warned us of it. He told us that light is a special case. It is not an object like any other object. When we use light in Relativity, we must take special care not to make false assumptions. This is what Postulate 2 means: "Take care! Light is not just another object. It is emitted at velocity c from all objects, no matter how they are moving themselves. You may not add your velocity to the velocity of light, not if you are travelling in the same line as the light, and not if you are travelling at an angle to the emission."
Therefore, the question, “where is the light right now?” is always a local question. If the light is in your eyes, you can say, “it is here.” Otherwise, you can say nothing. You cannot propose to diagram light from a distance, since your diagram is supposed to be a diagram of your data. You cannot diagram light from a distance, since there is no such data. You know only the information that light brings you, and when you receive this information the light is right in your eyes. Light in other fields is imaginary data, and if you try to diagram it you are sure to get into trouble. As a matter of data or of operation or of experience or of science, there is no such beast as “light in another field.” Light is always in the local field. That is what Einstein’s Second Postulate means.
We are finally ready to derive new transformation equations. Going in, we know two things. 1) The current equations are mathematically flawed. 2) They are not far off, since they have been verified by many experiments.
We have jettisoned two of the most important equations, including the first and central one, so it is difficult to see how to start. You can see why no one has wanted to work on this problem for a century. It goes beyond a subtle tinkering. Since the end result of the transformation equations has always been the ability to derive a relative velocity from a local velocity (or other known quantities), we should ask, what do these terms mean? What is a local velocity and what is a relative velocity? It turns out that these definitions are strictly practical. That is, these velocities are determined by how we measure them. Historically we have always measured velocity by one of two methods:
1) We measure our own velocity by using a clock and by measuring our change in x relative to a known background. As an example, if we were driving in a car (but did not have a built-in speedometer) we would have to make use of mile markers. We would take note of the markers as we passed them; and then, using our on-board clock, we would calculate the velocity. Please notice that in this case we see the markers from a negligible distance. The speed of light does not affect our calculation, because we are at mile marker x when we see mile marker x.
2) We measure the velocity of an object at some distance. This measurement is arrived at in a completely different way than the first one. Usually we are given x, as in the first problem. We know x because we have already marked it off, or we have it as an accepted number from previous experiments. But t is different. We use our own clock, it is true. But, because the object is at a distance, and because light has a finite speed, we do not see the object at the same time that the object sees itself.
To make this clearer, imagine that the object is a blinking light. In this case, there are actually two events. The object blinking, and our receipt of the blink. These two events take place x distance apart, and the gap in time is the time it takes for light to travel x.
Let us make up our own thought problem to illustrate this.
Thought problem one:
Apparatus:
1) A blinker that blinks at a rate of one blink per second.
2) A tunnel marked off with lines, like a ruler, to indicate distance.
3) An eye, with a clock that ticks at a rate of one per second, at the beginning of the tunnel.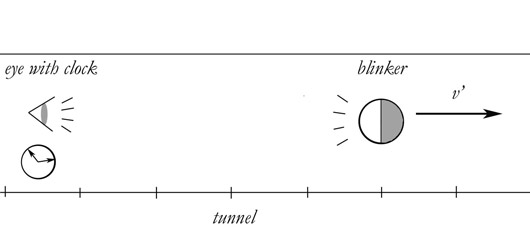
Experiment:
The blinker and the eye begin at rest, next to eachother. Their blinks and ticks are exactly synchronous. The blinker then takes off and goes through the tunnel at a constant velocity. It measures its own velocity based on the number of marks it passes for each blink. It reads the marks from a negligible distance. That is, it reads the marks as it passes them .
The eye also measures the velocity of the blinker. It measures the velocity of the blinker relative to its own clock. It measures by seeing the blinks, which are blinks of visible light. The eye is given x'. It has walked off the distance in a previous experiment (or you may want assume the eye is the one who painted the lines on the tunnel).
The blinker is set on a course directly away from the eye. Assume that it reaches v' instantaneously.
Question:
Will the eye and the blinker measure the same velocity?
If not, how can the velocity measured by the eye be known given the velocity as measured by the blinker itself (and vice versa)?
Answer:
Let t' = the period of each clock, from its own vicinity. This is the period measured when the two clocks are side by side at the beginning. Notice that the blinker is a clock. Each blink is a tick of the clock.
x' = distance blinker has gone relative to tunnel marks, according to its own visual measurements.
v '= velocity blinker is going, by it's own calculation.
Let t = period that the eye sees blinks from blinker. This gives us the apparent period.
v = velocity eye calculates blinker to be going, based on visual evidence.
This is the apparent velocity.
If you are with the blinker, then you will measure your own velocity like this
v' = x'/t'
Let us say that your first blink is at the 1km mark. Your second at the 2km mark, and so on.
Obviously, your v' = 1km/s
What then is v, the velocity of the blinker as measured by the eye?
To discover this, we must first find T1. That is, when does the eye receive the first blink, according to its clock?
t = period
T = time
Well, @ T1' = 1s,
x' = 1km, so the light must travel back to the eye 1km. It takes the light 1km/c to do this. So we would expect the eye to receive blink #1 at
T1 = T1' + (x'/c) = 1.000003s
And
@ receipt of second blink, T2 = 2.000006.
@ receipt of third blink, T3 = 3.00001.
and so on.
So, for a simple blinker, the general equation would be
Tn = T n ' + (xn' /c)
t = T2 - T1
t = t' + Δx'/c
A blinker with a period of 1s and a local velocity of 1km/s will appear to have period of 1.000003s.
This period will be stable.
Notice here the difference between my equation and Einstein's. From his paper of 1905 we find t = t' + Δx'/(c - v)
Einstein has subtracted a velocity from c, which is disallowed by his own Postulate Two. The correct equation is mine, which simply drops the v variable from the equation. We not need a given velocity to start with, as I have shown here; but if we are given one, it must be clear which system it belongs to. If it belongs to my blinker or Einstein's train, it should be labeled v'. If it belongs to my observer or Einstein's platform, then it is already a relative velocity. You can't discover it without a relative transform, as I am presently proving (x'/c is a transform).
Now let us calculate the apparent (or relative) velocity.
v = x'/t
= x'/[t' + (x'/c)]
= .999996km/s
You may say, "Wait, why did you use x' in that equation? And why did you assume x' = 1km when you said that the light must go 1km to get back to the eye, in the time equation? You can't assume these things! Relativity tells us that the clock will slow down and that x will shrink. x should be less than x'."
I am not assuming x' is the distance to use in the equation for apparent velocity. I am given it. The velocity of an observed object is either the given distance divided by the apparent time or the apparent distance divided by the given time. These are the only possible calculations for an observed velocity.
In the present case, v = x'/t or v = x/t' but not v = x/t
The same goes for the light ray traveling back to the eye, in the time equation. x' is simply a given here, just as c is a given. Without them, any equations—mine or Einstein's—would be useless.
If I was not given x' (or v' and t', which is the same thing), there is no way I could know it or calculate it. And there is no way I could calculate v.
Think of it this way: A train passes at night. We don't know the velocity, and we can't see the mile markers. All we can see is a pulse clock on the train. Can we know its velocity relative to us? No. The Lorentz transformations, as used up to now, can tell us nothing. We must be given a local velocity v', or we must know x'. The apparent velocity of the pulse clock is determined by its period and its speed. That is, it could be ticking slowly and going slowly, or ticking faster and going faster: in both cases it would look the same.
It is true, though, that x will look shorter to the observer, as Einstein said. But this x is not x'. Nor is it the x used in the apparent velocity equation, as I have shown. That x is given as x'. What we are seeking for x here is the apparent distance.
It is calculated like this:
apparent x = (apparent v)t'
If you are still unclear on why I used t' instead of t, think of it this way. What we want is to multiply the apparent velocity v by the time on our clock, right? We want to know what x is at T1 , and T2 , and so on, on our own clock. That is what it means to measure by your own clock. If you know a runner's speed, and want to calculate how far he runs in a time interval, you would not check where he was as your watch ticked 1.000003, would you? You calculate using your standard time interval, your own second hand.
You may say, "But you have defined t as the time for the eye, and t' the time for the blinker. Now you want to switch." No. I never defined t as the time for the eye. Look above. I defined both initial times as t'. The local time is t', for both the blinker and the observer. I calculated t to be the apparent period of the blinker, as measured by the eye. This does not mean that the eye's clock is ticking every 1.000003 seconds. It means, of course, that the blinker's clock looks like it is ticking every 1.000003 seconds, from the eye. But the eye's clock is ticking at a normal interval, for the eye; just as the blinker's clock is ticking at a normal interval, for the blinker. This normal interval—the rate a clock goes as seen from its own vicinity—I have defined as t'.
Notice that if the eye's clock had a period of t, then it would not see the blinker's clock as slow. It see's the blinker's clock as having a period of t, right? If the eye's clock also had a period of t, there would be no difference. The blinker's clock is slow, relative to the eye's clock, which therefore is not slow. Very simple.
So, @ T' = 1,
v = .999996km/s.
And x = .999996km/s = .999996km.
1s
This is just what we would expect.
t has apparently slowed down. And x has apparently shrunk. That much is consistent with Einstein, at least.
But you can see that we have had to be very careful about our t's and x's and v's. You cannot just substitute an x or a t into an equation because it looks similar to another x or t. You must think about what is really happening.
So, to sum up:
The blinker's period will appear to slow down, but the period will remain stable (it will not continue to slow down further the farther away it gets).
Therefore, the velocity will also appear to be slow. If the blinker sends you a message telling you that its v' is 1km/s, then it will have appeared to slow down relative to that.
If the blinker has a length along the x-axis, then the blinker will be calculated to appear shorter, because there is an apparent contraction along the x-axis. If you measured the blinker when it was at rest next to you, then your calculation will be short relative to that.
We have found that x = vt'
and v = x'/t
so, x/t' = x'/t
and xt = x't' just as Relativity predicted.
x and t are inversely proportional. As t appears to get larger, x appears to get smaller
By substituting quantities we can now easily derive the direct transformation equations, and calculate v from v' or x from x' and v':
v = x'/t = x/t'
t = t' + (x'/c)
= t' + (v't'/c)
= t' (1 + v'/c)
v = x'/[t'(1 + v'/c)]
x' = v't'
v = v'
1 + (v'/c)
v' = v
1 - (v/c)
x = x'
1 + (v'/c)
Now that we have our new equations, I predict this complaint: "You are assuming that t and x are absolute, before you even start. Your marked off tunnel is an absolute system of coordinates, and your t's even coincide. They may appear to be .000003s apart, but they are really the same. Relativity does not rely on these assumptions. It transcends them."
My answer is that I have done precisely what Einstein did. I started with given quantities and derived unknowns from them by discovering the proper equations. You are calling my givens "absolutes," but the terminology is meaningless. They are not absolutes, they are accepted values. Einstein does not derive his relative velocities from thin air. In his transformation equations, you must have certain information to start with. I claim that my givens are no more absolute than his. My givens are exactly the same as his. If my elucidation of his process makes you think that these givens are absolutes, then I can force you to admit that Einstein's givens are also absolutes.
In fact I will do so now. Einstein says (p.18, Rel.) that the train has a given velocity v. The implication is that this velocity is a local velocity. It must be the velocity of the train, as measured from the train. He cannot mean the velocity of the train as measured from the embankment. For if he meant as measured from the embankment, then we would already be given a relative velocity, and we would not need fancy transformation equations to find it.
Einstein then shows, correctly, that the train's clock will look slow to the eye on the embankment and that the train's measuring rods will look short. And he presents the Lorentz equations for t and x. But then he never uses his relative x and t, that he derives by these equations, to calculate a relative v. Isn't this strange? He never concludes that there is a relative v that is different than the v given in the problem. He derives two t's and two x's, but never derives the second v, the relative v.
Later, he derives the Lorentz transformation for velocity, using his t and x equations (Ch.8, on Fizeau). But this is for the addition of velocities. It is for the situation in which the man on the train is moving relative to the train and the train is moving relative to the embankment (eye). You have two relative velocities and you want to find the third. This equation gives us a velocity of two degrees of relativity. The velocity that this equation yields is the velocity of the man as seen by the embankment. But this is not the same as the velocity of the train.
If Einstein had derived this relative velocity for the train as seen from the embankment, then it would have been clear that something was wrong. He would then have to admit that the given v (in equation x' = x - vt) was the velocity of the train as measured by the train. And if he admitted this, then he would have to admit that this velocity was measured relative to the tracks. And if he did that, then he would have to defend himself against the charge that he had already assumed an absolute co-ordinate system, just like I am having to do. But in Einstein's explanation, it never comes up. He never defines his terms, and no one has ever asked him to. No one, til now, has ever asked what the given v is, precisely, and how it is determined.
The given v must be the v of the train relative to the tracks, as measured from the train. Einstein must be given this velocity before he ever starts: relative v is dependent on v'. So Einstein must have his railroad track already marked off before he can calculate his relative x and t.
He even admits this. At the top of the same page (p. 18) he says, "Of course we must refer the process of the propagation of light (and indeed every other process) to a rigid reference body (co-ordinate system)." [his parentheses]
His problem implies the existence of a pre-existing system, like my tunnel. His pre-existing system is his traintrack. But this system remains hidden throughout the problem. Regardless, this system—whether his or mine—is not an "absolute." It is not an absolute in the sense of contradicting the relativity of measurement. It is a given, a postulate that allows for the calculation of unknowns.
You may be interested to know that Feynman also admitted the existence of what you are calling the "absolute" field. He called it the "proper" field, and the time the "proper time." This is just the local field, and Feynman admitted that all local fields were equivalent. They have to be in order to do any sort of calculations, of any kind.
You may say, "Yes, but there are two co-ordinate systems (S and S'). Distance in one will not be the same distance in the other. x does not equal x'. You cannot just transfer x' into your equation—as you did when the blink was traveling from the blinker to the eye—as if you already knew the distance."
Einstein did.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.