|
go to homepage
go
to updates
The Discovery
of First-Degree Relativity
and the Refutation of Gamma
by
Miles Mathis

First written
June 2001 as a compression of my longer original
paper of November 2000. One or the other was submitted in
2001-2002 to PRL, ADP, CERN, Nature, and JPL, where it was either
refused or ignored. For example, it was submitted November 2001
to Annalen
der Physik
and refused January 2002. I have the letter from Ulrich Eckern in
my files. The original paper was submitted to PRL even before
that, since it was refused in the summer of 2001.
Introduction
to the Problem
Special
Relativity is widely considered one of the most famous physical
theories in history, as well as one of the most perfect. Quantum
mechanics, or QED, the only other theory that is as famous, has
been corrected a countless number of times in the 20th century.
In that time, Special Relativity has not been corrected once.
Einstein's derivations of 1905 stand to this day. Gamma
and the addition-of-velocity equation have never been corrected.
They are considered uncorrectable. They underlie the final
equations of four-dimensional space (Minkowski) and the field
equations of General Relativity. The tensor calculus takes them
as given.
However in recent decades there have been a number of
discrepancies found in the use of the equations on data from both
accelerators and space satellites. Physical Review Letters
published several papers on the satellite problem (the so-called
Pioneer Anomaly) of the Jet Propulsion Lab a few years ago. It
was never solved to everyone's satisfaction, using the mechanical
analyses offered. I became convinced at that time, and remain
convinced, that the problem is in the basic equations. So I have
returned to the original derivations of nearly a century ago. I
have concentrated on the algebraic derivations, ignoring the
tensor calculus that was imported into the problem later. The
tensor calculus is a math designed to handle a large number of
variables, using matrices and other time-saving devices. It is
not a good math to use for simple conceptual problems, concerning
only a few linear variables. The tensor calculus unnecessarily
makes a very dense theory even more difficult. It is supremely
difficult, for instance, to properly analyze the basic
conceptions of the theory, which are spatial and temporal, when
you don't have a time variable, labeled as such. Tensor calculus
may be a necessity in the field equations of General Relativity,
but in Special Relativity it is more math than the job requires.
This is especially true in the initial derivations, where the
velocity has no angle to the x-axis, and there are no other
mathematical complications.
In its inception, the math of Special Relativity was algebra.
Except for one step, Einstein's 1905 derivations1 of
both gamma (γ) and the addition-of-velocity equation were
algebraic. Even this one step of calculus was unnecessary, as
Einstein proved in the appendix to his book Relativity,
where he did without it. This is not surprising, since in both
places the problem concerns linear uniform motion.
After studying
Einstein's various algebraic derivations closely for several
years, I am now in a position to prove that his final equations,
though close enough for much prediction, are not correct. He
ignores one very important step, and this step completely
compromises the math. Nor was this step uncovered in later
emendations. All current derivations yield equations for two
degrees of relativity. First-degree relativity is ignored. This
paper is my announcement of the discovery of First-Degree
Relativity. I rush to add that in correcting Special Relativity,
I am not proposing a return to classical mechanics. Nor am I
questioning the basis for time dilation. This paper is in no way
a refutation of Relativity, as a whole, nor a dismissal of the
need for transformation equations. I simply offer subtle
corrections to the existing mathematics. My transformation
equations match Einstein's, in form and theory, but they provide
small differences at high speeds and distances. This solves the
Pioneer Anomaly, as well as several other outstanding problems.
Part One
The
Primary Error
Relativity is
caused by motion. An object in motion relative to a second object
no longer shares the co-ordinate system of that object. We must
therefore create two systems to explain them. Specifically, the
length and time variables will differ, and at least one
transformation equation will be required to go from one to the
other. The transformation equation(s) must include the speed of
light, since the finite speed of light is what makes them
necessary in the first place. If c were infinite, then all space
would be one co-ordinate system, as with Galileo. This is
Einstein's set-up, which I fully accept. It implies that clocks
and measuring rods will not match up across systems. The result
is length contraction and time dilation, which I also do not
question.
In the 1905 paper, Einstein gives us two systems, K and k. K is
at rest, k is moving. Then we are given a constant velocity,
v—that is k relative to K (v is linear, along the x-axis). We
are also given x and t in K, and ξ and τ in k. We seek the
transform between them. This is all we are given involving K
relative to k, but the first mistake has already been made.
What is wrong is that
Einstein failed to assign the given v to either K or k. If the
clocks and measuring rods in K are different from k, then K and k
will measure velocity differently. That is, they must get
different numbers for the velocity of k. But Einstein did not
notice this. He did not notice that v, as given, is already a
relative velocity. No one else has noticed this in 99 years. In
this problem, we should have the velocity of k relative to K,
measured from K; and the velocity of k relative to K, measured
from k. One motion, two different numbers.
This is what I call First-Degree Relativity. We have a v and a v'
now, and we need a transformation equation from one to the other.
How can we get this?
First, let me clarify the situation. I know that some will say
here that k has no velocity measured from k. Velocity is a
relative term, one that requires a background against which to
measure. This is true. k has no velocity relative to k. But k
does have a velocity relative to K, and k can easily measure that
velocity itself.
v = velocity of k rel K as measured from
K.
v' = velocity of k rel K as measured from k.
But
before I show you the math for achieving a transform from v to
v', we must visit Einstein's equations, to see precisely what
went wrong there. I suspect that few will have the fortitude to
wade through my new derivations until they are convinced beyond a
doubt that the current equations of Einstein are faulty. Whether
or not you know of the various anomalies that have arisen in
experiments, I can show you right now that Einstein's equations
cannot possibly work, due to simple mathematical errors.
First of all, notice
that Einstein has no transformation equation to go from v to v'.
None at all. The v transform of Special Relativity is
V =
v + w
1 + (vw/c2)
This
is a compound velocity, as is easily seen by counting the number
of velocity variables. In order to calculate V, you must be given
v and w. According to Einstein's famous thought experiment with
the train, v is the same as our v above. It is the velocity of
the a train going by on a platform. We are on the platform. In
this case, w is the velocity of a man walking away from us in the
train. V is then the velocity of the walking man relative to us
on the platform. But Einstein never derives an equation to go
from v to v'. This is because v' is not equivalent to any of the
variables above. As you can see,
V = velocity of man
measured by platform
v = velocity of train measured by
platform
w = velocity of man measured by (man or train?)
v'
= velocity of train measured by train
Einstein has no v',
so he cannot possibly calculate it. Special Relativity, as it now
stands, does not recognize the existence of v'. This compromises
all its equations. Put very simply, Einstein has too few
coordinate systems. In the velocity transformation equation
above, he has three velocity variables. But he tries to calculate
these from only two coordinate systems. In order to do this he is
forced to transfer variables across systems, and he does this
illegally, as I will show.
[Subsection added 10/2009]
Professional physicists have ignored the above analysis, telling
me that SR is known to be symmetrical, by Einstein's first
postulate: "The laws of electrodynamics and optics will be
valid for all frames of reference for which the equations of
mechanics hold good." That is Einstein's wording of it from
the 1905 paper. These physicists tell me that the starting
velocity is symmetrical, which is why we have no v'. If I measure
your velocity as v, you will measure mine as v. That is true.
Under that physical transform, velocity is symmetrical. But you
must see that the equations of Special Relativity are not written
for that specific transform. SR is not transforming your
measurement of me to my measurement of you. It is transforming my
measurement of me to your measurement of me. In fact, if SR were
symmetrical, we would need no transforms at all. If SR were
really symmetrical in this way, we would need no t' or x' either.
The actual transformational equations of SR are transforming
local measurements into measurements at a distance, and there is
no symmetry between those operations of measurement.
Yes,
Einstein's postulate 1 is correct, if it is read correctly. The
mechanical laws are valid in all frames, and you can take
any frame you like as being at rest. In this sense, the laws
are symmetrical. But if the operation of measurement is not
symmetrical between these systems, then the transforms cannot be
symmetrical either. That is, the laws are always symmetrical, but
the “equations of mechanics” are symmetrical only when the
physical operations between the systems are analogous. In
transforming length and time in one system to another, the
operations are not analogous. In Einstein's transformations, we
choose quite freely to measure from one system or the other. Once
we do, the symmetry is broken, because the measured system is not
measuring us back. The transform is between “local numbers”
and “measured-at-a-distance numbers.” There is no symmetry
between those numbers.
This means that although
Einstein's postulate 1 is still correct and valid, the velocity
is not symmetrical across the transforms. Yes, there is a
symmetry between “you measure my velocity” and “I measure
your velocity”, but you are not measuring my velocity in the
transforms. You are also not measuring my time or length or
distance traveled. All the measuring is going in one direction
only. For this reason, we do have two velocities from the
start, v and v', and they are not the same number.
Part
Two
Another Central Error
But let us
start at the beginning. Let us start with an
illustration.
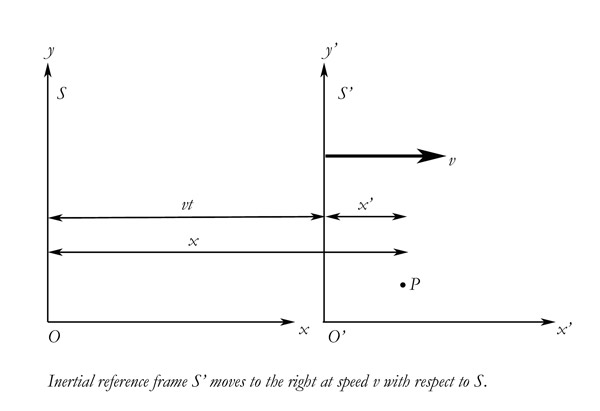
This
illustration is typical of current textbook illustrations. It is
the attempt to diagram Einstein's train thought problem from the
book Relativity, and here the artist has tried to graph
x', x, and vt. [To make things a bit easier, for the book
Relativity Einstein exchanged the Greek variables in the
1905 paper for primed variables. I will do the same in the
equations that follow.] The man is at point P. We, the observers,
are understood to be watching from the embankment.
In the
first part of the problem, the man is not moving inside the
train: x' is simply the distance of the man from the origin at
t0. We are transforming the distance, not the
velocity. We transform the velocity variable later, when the man
also moves inside the train. Einstein makes this very clear in
the paper of 1905, and it is obvious regardless. There is only
one velocity variable given. If the man were moving relative to
the train, we would have to be given that velocity as well, as
you can see.
To go with this thought experiment, Einstein
gives us this equation (p.33, Rel.),
x' = x - vt
In his
original paper of 1905 ["On the Thermodynamics of Moving
Bodies"], he gives the same equation. But neither there nor
in the book Relativity does he say where this equation
comes from. In the 1905 paper, the equation is completely
mysterious; but in Relativity he gives us a clue. Einstein
says, "If in the place of law of the transmission of light
we had taken as our basis the tacit assumptions of the older
mechanics as to the absolute nature of times and lengths, then
instead of the above we should have obtained the following
equations:
x' = x - vt
y' = y
z' = z
t' =
t
"This system of equations is often termed the
'Galilei transformation.' The Galilei transformation can be
obtained from the Lorentz transformation by substituting an
infinitely large value for the velocity of light c in the latter
transformation." Einstein also called these equations an
expression of "Newton's Principle of Relativity."
Before Special Relativity, we transformed from one coordinate to
another using these equations, he implies.
But this is not the case. There is no such thing as a Galilei
transformation equation. For Galileo and Newton, no
transformation was necessary for a linear problem like this. x in
S' would equal x is S. Besides, the whole universe was a single
co-ordinate system for Galileo, and the train would not have been
given a system of its own. There is no possibility of a prime
variable of this sort in a Galilei system. The only time that two
Galilei systems would have two x variables is in a case where the
two systems have different origins. The equation in that case
would be something like x' = x - a, where a is the
distance between the two origins. In Einstein's thought problem
the origins are overlapping at t0. This is one of the
givens. In the paper of 1905 he states outright that the origins
are equal at t0. He is not trying to calculate the
distance from one system to another, he is trying to export a
distance in one system to another system.
This being so,
the equation x' = x - vt cannot be applicable to the problem. For
you can see that the true list of Galilei transformations are
these.
x' = x
y' = y
z' = z
t' = t
The
velocity has absolutely nothing to do with a Galilei
transformation. If c is infinite, then all measurers will measure
equal times, distances and velocities. x' = x, v' = v. This is
because there is no difference between what I see and what the
train sees. Light brings me exactly the same information that it
brings the train, at exactly the same time. There can be no
transformation equation: not a fancy Lorentz transformation, but
also not a simple transformation like x' = x - vt .
Einstein has used the wrong first equation. Let us look at
what the equation is telling us, in a specific example. Let's say
at t0 the back end of the caboose is at the origin of
the moving system, S'. Let's also say that x' is the distance to
the front of the same caboose, as measured from inside the
caboose. The whole train then leaves us at the station and
travels a distance given by the term vt. The equation x = x' + vt
is telling us that we, back at the station, will measure the
length of the caboose as "how long the caboose is, measured
from the caboose" + "the distance it has gone". As
if we will add the length of the traintracks to the length of the
caboose! Do you see now how utterly absurd this is? It assumes
that we can't see, with our own eyes, that the back of the
caboose has also traveled vt, and must therefore be subtracted
from x' + vt. What we are looking for in this problem is simply
"how long the caboose looks to us." This equation tells
us nothing about that at all, neither classically nor
relativistically. It is the wrong equation. Classically, the
correct equation is just x' = x. Einstein imported an equation
that Galileo would have used to find the total distance from the
origin to the front of the caboose after time t, and applied it
to find the length of the caboose as seen from the origin. An
absolutely momentous blunder.
If light has an infinite speed, then the embankment will see both
ends of any rod at the same time. The embankment will also see
the back of the train and any other point on the train at the
same time. So Einstein's given equation cannot be a Galilei
transformation, in any sense. This mistake has never been
corrected (I just saw the very same equation used by Richard
Feynman to prove Special Relativity in Six Not-so-Easy
Pieces—92 years after Einstein). Physics textbooks still
use Einstein's series of conceptual steps to prove the equations
of Special Relativity.
This is the current derivation in physics textbooks:
Assume
x' = x - vt
Assume that the transformation from Galilean equations to
Relativistic equations will be linear.
Then
Step 1:
x' = γ(x - vt) where γ is the transformation term we
seek.
and x = γ(x' + vt')*
Now, says Einstein (following Lorentz), light travels in these
coordinate systems (S and S') in this way:
Step
2:
x = ct and
x' = ct'
Substituting the first equations into these
equations gives us:
Step 3:
ct = γ(ct' + vt') = γ(c + v)t'
and
ct' = γ(ct - vt) = γ(c - v)t
If we
substitute t' from the second equation into the first, we find
that
Step 4:
ct = γ(c + v)γ(c - v)(t/c) = γ2(c2 -
v2)(t/c)
Cancel out the t on each
side and solve for γ:
Step
5:
γ = 1/(1 -
v2/c2)1/2
This is the
famous transformation term gamma. The math leading
up to it is correct, but it doesn't matter, since the assumption
was incorrect. You cannot start from a false equation and derive
a true equation.
*Einstein used the equation
x = γ(x' + vt)—without the t primed. But current physics
textbooks have changed the notation in order to make gamma
derivable with an internally consistent series of steps, as
above. The math is correct; the postulates and givens are not.
Part Three
The
Third Error
This leads us
to the third major problem. Everyone knows that Einstein used the
Lorentz equations to find that time appeared to slow down and x
appeared to get shorter. Length contraction and time dilation.
But let's look for a moment at the two light equations above. The
light equations Lorentz and Einstein both used:
x = ct
x'
= ct'
If these are true,
then c = x/t
from the first of these equations
and
x' = xt'/t by substitution
so
x'/x = t'/t
This means that in these equations the apparent change in x is
proportional to the apparent change in t.
But when time slows down (in any system, or by any means of
measurement), the period gets larger. Time slowing down
implies a larger t, not a smaller t.
That is, t should appear to get larger as x appears to get
smaller. Einstein even states this outright, in the book
Relativity. He says (Ch.XII, p. 37) "As judged from
K, the clock is moving with the velocity v ; as judged from this
reference body, the time which elapses between two strokes of the
clock is not one second but [γ] seconds, i.e. a somewhat larger
time. As a consequence, the clock goes more slowly than when at
rest." Again, he says "a somewhat larger time."
Physicists have focused on the sentence after that, up to now.
But time is not defined by the rate of the clock, not even by
Einstein. Or stated more precisely, time is not measured that
way. Relativity is primarily a theory of measurement, and so what
is required is an operational definition of time. Not what time
is as an abstract concept, but what time is as a measured
quantity. Time is the length of the period, as Einstein flatly
states here. A second is not a stroke of the clock. A second is
the gap between strokes. Time is not the strokes of the clock, it
is the time between strokes of the clock. As he says, a moving
clock is seen by a stationary observer to have a period γt,
which is larger than t. A dilated clock ticks slower because its
period is longer.
[To
consider this question further, see the links at the end of the
paper—a discussion of this definition with several scientists
and mathematicians, and a paper on the operational definition of
time.]
As
further proof of this very important concept, I refer you to the
The Meaning of Relativity again. In Chapter 2 he provides
this equation (eq. 22a):
Σ Δxv'2 - c2Δt'2 =
0
Conceptually this is obviously analogous to the equation x' =
ct'. Einstein is just varying his math a bit, dressing it up. The
thing to notice here is the delta t. He has now made it clear
that he is referring to changes in time, not instants in time. In
these equations, the variable refers to the time period, not the
instant in time. Which is precisely my point. When time slows
down the period gets larger.
This being true, x and t must be in inverse proportion!
So,
we should find that
x/x' = t'/t t = t'x'/x
x = x't'/t
or xt =
x't'
And, if x' = ct'
then c =
xt/t'/t'
and x = ct'
2/t
Only if t = t' does
t2/t' = t'
Einstein states that t does not
equal t'
therefore x does not equal ct
Even the light equations were wrong!
Part Four
New
Transformation Equations
We are
finally ready to derive new transformation equations. Going in,
we know two things. 1) The current equations are mathematically
flawed. 2) They are not far off, since they have been verified by
many experiments.
We have jettisoned two of the most important equations, including
the first and central one, so it is difficult to see how to
start. You can see why no one has wanted to work on this problem
for a century. It goes beyond a subtle tinkering. Since the end
result of the transformation equations has always been the
ability to derive a relative velocity from a local velocity (or
other known quantities), we should ask, what do these terms
mean? What is a local velocity and what is a relative
velocity? It turns out that these definitions are strictly
practical. That is, these velocities are determined by how
we measure them. Historically we have always measured
velocity by one of two methods:
1) We measure our own velocity by using a clock and by measuring
our change in x relative to a known background. As an
example, if we were driving in a car (but did not have a built-in
speedometer) we would have to make use of mile markers. We
would take note of the markers as we passed them; and then, using
our on-board clock, we would calculate the velocity.
Please notice that in this case we see the markers from a
negligible distance. The speed of light does not affect our
calculation, because we are at mile marker x when we see mile
marker x.
2)
We measure the velocity of an object at some distance. This
measurement is arrived at in a completely different way than the
first one. Usually we are given x, as in the first
problem. We know x because we have already
marked it off, or we have it as an accepted number from previous
experiments. But t is different. We use
our own clock, it is true. But, because the object is at a
distance, and because light has a finite speed, we do not see the
object at the same time that the object sees itself.
To make this clearer, imagine that the object is a blinking
light. In this case, there are actually two events.
The object blinking, and our receipt of the blink. These
two events take place x distance apart, and the gap in time is
the time it takes for light to travel x.
Let us make up our own thought problem to illustrate
this.
Thought problem one:
Apparatus:
1) A blinker that blinks at a rate of one blink per
second.
2) A tunnel marked off with lines, like a ruler, to indicate
distance.
3) An eye, with a clock that ticks at a rate of one per second,
at the beginning of the tunnel.
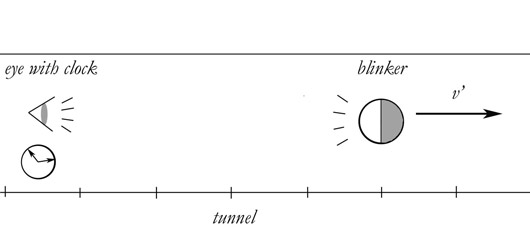
Experiment:
The blinker and the eye begin at rest, next to eachother.
Their blinks and ticks are exactly synchronous. The blinker
then takes off and goes through the tunnel at a constant
velocity. It measures its own velocity based on the number
of marks it passes for each blink. It reads the marks from
a negligible distance. That is, it reads the marks as it
passes them .
The eye also measures the velocity of the blinker. It
measures the velocity of the blinker relative to its own clock.
It measures by seeing the blinks, which are blinks of visible
light. The eye is given x'. It has walked off the
distance in a previous experiment (or you may want assume the eye
is the one who painted the lines on the tunnel).
The blinker is set on a course directly away from the eye.
Assume that it reaches v' instantaneously.
Question:
Will the eye and the blinker measure the same
velocity?
If not, how can the velocity measured by the eye be known given
the velocity as measured by the blinker itself (and vice
versa)?
Answer:
Let t' = the period of each clock, from its own vicinity.
This is the period measured when the two clocks are side by side
at the beginning. Notice that the blinker is a clock.
Each blink is a tick of the clock.
x' = distance blinker has gone relative to tunnel marks,
according to its own visual measurements.
v '= velocity blinker is going, by it's own calculation.
Let t = period that the eye sees blinks from blinker.
This gives us the apparent period.
v = velocity eye calculates blinker to be going, based on visual
evidence.
This is the apparent velocity.
If you are with the blinker, then you will measure your own
velocity like
this
v' = x'/t'
Let us say that your first blink is at the 1km mark. Your
second at the 2km mark, and so on.
Obviously, your v' = 1km/s
What then is v, the velocity of the blinker as measured by the
eye?
To discover this, we must first find T1.
That is, when does the eye receive the first blink, according to
its clock?
t = period
T = time
Well, @ T1' = 1s,
x' = 1km, so the light must travel back to the eye 1km. It
takes the light 1km/c to do this. So we would expect
the eye to receive blink #1 at
T1 = T1' + (x'/c) =
1.000003s
And
@ receipt of second blink, T2 = 2.000006.
@ receipt of third blink, T3 =
3.00001.
and so on.
So, for a simple blinker, the general equation would
be
Tn = T n ' + (xn' /c)
t = T2 - T1
t = t' + (Δx'/c)
A blinker with a period of
1s and a local velocity of 1km/s will appear to have period of
1.000003s.
This period will be stable.
Now let us
calculate the apparent velocity.
v = x'/t
= x'/[t' + (x'/c)]
= .999996km/s
You may say, "Wait, why
did you use x' in that equation? And why did you assume x'
= 1km when you said that the light must go 1km to get back
to the eye, in the time equation? You can't assume these
things! Relativity tells us that the clock will slow down
and that x will shrink. x should be less than
x'."
I am not assuming x' is the distance to use in the equation for
apparent velocity. I am given it. The velocity of an
observed object is either the given distance divided by the
apparent time or the apparent distance divided by the given
time. These are the only possible calculations for an
observed velocity.
In the present case, v = x'/t or
v = x/t' but not
v = x/t
The same goes for the light ray traveling back to the eye, in the
time equation. x' is simply a given here, just as c is a
given. Without them, any equations-- mine or Einstein's--
would be useless.
If I was not given x' (or v' and t', which is the same thing),
there is no way I could know it or calculate it. And there
is no way I could calculate v.
Think of it this way: A train passes at night. We
don't know the velocity, and we can't see the mile markers.
All we can see is a pulse clock on the train. Can we know
its velocity relative to us? No. The Lorentz
transformations, as used up to now, can tell us nothing. We
must be given a local velocity v', or we must know x'. The
apparent velocity of the pulse clock is determined by its period
and its speed. That is, it could be ticking slowly and
going slowly, or ticking faster and going faster: in both cases
it would look the same.
It is true, though, that x will look shorter to the observer, as
Einstein said. But this x is not x'. Nor is it the x
used in the apparent velocity equation, as I have shown.
That x is given as x'. What we are seeking for x here
is the apparent distance.
It is calculated like this:
apparent x = (apparent v) X t'
If you are still unclear on why I used t' instead of
t, think of it this way. What we want is to multiply the
apparent velocity v by the time on our clock, right?
We want to know what x is at T1 , and T2 ,
and so on, on our own clock. That is what it means to
measure by your own clock. If you know a runner's speed,
and want to calculate how far he runs in a time interval, you
would not check where he was as your watch ticked 1.000003, would
you? You calculate using your standard time interval, your
own second hand.
You may say, "But you have defined t as the time
for the eye, and t' the time for the blinker.
Now you want to switch." No. I never defined
t as the time for the eye. I calculated
t to be the apparent period of the blinker, as measured by
the eye. This does not mean that the eye's clock is
ticking every 1.000003 seconds. It means, of course, that
the blinker's clock looks like it is ticking every 1.000003
seconds, from the eye. But the eye's clock is ticking at a
normal interval, for the eye; just as the blinker's clock is
ticking at a normal interval, for the blinker. This normal
interval—the rate a clock goes as seen from its own vicinity—I
have defined as t'.
Notice that if the eye's clock had a period of t, then it would
not see the blinker's clock as slow. It see's the blinker's
clock as having a period of t, right? If the eye's clock
also had a period of t, there would be no difference. The
blinker's clock is slow, relative to the eye's clock, which
therefore is not slow. Very simple.
So, @ T' = 1,
v = .999996km/s.
And x = .999996km/s =
.999996km.
1s
This is just what we would expect.
t has apparently slowed down. And x has apparently
shrunk. That much is consistent with Einstein, at
least.
But you can see that we have had to be very careful about our t's
and x's and v's. You cannot just substitute an x or a t
into an equation because it looks similar to another x or t.
You must think about what is really
happening.
So, to sum up:
The blinker's period will appear to slow down, but the period
will remain stable (it will not continue to slow down further the
farther away it gets).
Therefore, the velocity will also appear to be slow. If the
blinker sends you a message telling you that its v' is 1km/s,
then it will have appeared to slow down relative to
that.
If the blinker has a length along the x-axis, then the blinker
will be calculated to appear shorter, because there is an
apparent contraction along the x-axis. If you measured the
blinker when it was at rest next to you, then your calculation
will be short relative to that.
We have found that
x = vt'
and v = x'/t
so, x/t' = x'/t
and xt = x't' just as Relativity predicted.
x
and t are inversely proportional. As t appears to get
larger, x appears to get smaller
By substituting
quantities we can now easily derive the direct transformation
equations, and calculate v from v' or x
from x' and v':
v = x'/t = x/t'
t = t' + (x'/c)
= t' + (v't'/c)
= t' (1 + v'/c)
v = x'/[t'(1 + v'/c)]
x' = v't'
v = v'
1 + (v'/c)
v' = v
1 - (v/c)
x =
x'
1 + (v'/c)
Or, to restate that last equation: x' = x/(1 - v/c). In this
equation, you can see that the transformation term 1/(1 - v/c)
can also be written c/(c - v). This is interesting because in the
paper of 1905 Einstein found the transformation term to be c 2
/(c2 - v2). He improperly reduced it to
1/√(1 - (v2/c2), the current value for
gamma. c2/(c2 - v2)
correctly reduces to 1/[1 - (v2/c2)]. There
is no square root. This has also never been corrected, or even
commented on3. However, it does not matter, since I
have now proved that both values for gamma are wrong. The
transformation term for one degree of relativity is simply 1/(1 -
v/c). This term applies when we are transforming the numbers on
the train to the numbers on the platform. It does not apply to a
man walking inside the train. It applies to the train itself.
You
may think that the transformation term for two degrees may be
gamma with or without the square root, since c2/(c2
- v2) is a sort of doubling of my term. But I will now
go on to derive the velocity transform for the man walking inside
the train—the velocity transform for two degrees of
relativity—and in doing so I will show that gamma does
not apply there either, not with the square root nor without it.
Part
Five
Second-Degree Relativity
First I will
show why Einstein's proof does not work. In his 1905 paper he did
not differentiate his ξ equation in order to find his relative
velocity equation, like they do now in textbooks. He simply
combined his equations algebraicly, like this:
From earlier in the paper Einstein found:
γ = gamma
= 1 /√(1 - v2/c2)
τ = γ(t -
vx/c2)
ξ = γ(x - vt)
Now he says, if a point
is moving in k,
let ξ = w(τ) where w "is a constant".
Notice two things. One, Einstein now has a point moving in k
instead of a light ray. Two, he does not define this new velocity
variable w at all, beyond saying it is a constant.
By
substitution, he gets,
w(τ) = γ(x - vt)
wγ(t - vx/c2)
= γ(x - vt)
gamma cancels out
wt - wvx/c2 = x - vt
x
+ wvx/c2 = wt + vt
x(1 + wv/c2) = (w +
v)t
x = ( w + v )t/[1 + wv/c2]
Now, watch
this last step very closely. He reduces the above equation to:
V
= w + v
1 +
wv/c2
This is the current value for V. This
equation stands to this day.
But to reduce like he did he must
assume that V = x/t
We were given that w = ξ/τ
So what
does v equal? v is what x over what t?
V = x/t
w =
ξ/τ
v = ?/?
You may say, well maybe the x is x'.
Maybe, but what is the t? He has no third t-variable anywhere, in
this paper. And in later derivations, when he does have a t', he
has no τ. He never has three t variables. What we need to solve
for an addition of velocities, amazingly enough, is four
t-variables.
t0 = the time of K from K
t =
the time of the point as seen from K
t' = the time of k as
seen from K
t'' = the time of k as seen from k
τ = the
time of the point as seen from k.
τ' = the time of the point
as seen from the point
but t" = τ' = t0
We
need five x-variables
x = displacement of the point, as
measured by K
x' = displacement of k, as measured by K
x"
= displacement of k as measured by k.
ξ = displacement of
the point, as measured by k
ξ' = displacement of the point
as measured by the point
Einstein says that v is the
velocity of k relative to K.
w is the velocity of a point
relative to k.
V is the velocity of that point relative to
K.
but to solve we also need,
w' = velocity of the point
measured by the point
v' = velocity of k as measured by k
w'
= ξ'/t0
v' = x"/t0
τ = t0
+ ξ'/c
w = ξ'/(t0 + ξ'/c) = w'/(1 + w'/c)
w'
= w/(1 - w/c)
v = x"/t'
t' = t0 + x"/c
v
= x"/(t0 + x"/c) = v'/(1 + v'/c)
v' =
v/(1 - v/c)
t = t0 + (ξ' + x")/c)
V = (ξ'
+ x")/t = (ξ' + x")/[t0 + (ξ' +
x")/c)]
{eq.5} V = v'
+ w'
1 + [(v' + w')/c ]
V =
v
+
w
1 - (v/c)
1 - (w/c)
v
+ w
1 + 1
- (v/c)
1 - (w/c)
c
=
v + w - (2vw/c)
1 -
v/c - w/c + vw/c 2 + [v + w - (2vw/c)]/c
V =
v + w - (2vw/c)
1 - vw/c2
Just to be
sure that gamma does not apply to the transformation of
two degrees for t, let us find τ' in terms of v, like Einstein
did.
t = t0 + (ξ' + x"/c)
w' = ξ'/t0
and v' = x"/t0
t = t0 + (w't0+
v't0)/c
w' = w/(1 - w/c) and v' = v/(1 - v/c)
t
= τ' + wτ'/c(1 - w/c) + vτ'/c(1 - v/c)
t = τ'{1 + [w/c(1 -
w/c)] + v/c(1 - v/c)}
t/τ' = (1 - w/c)(1 - v/c) + (1 -
v/c)w/c + (1 - w/c)v/c
(1 - w/c)(1 - v/c) (1 - w/c)(1 - v/c) (1
- w/c)(1 - v/c)
= 1 - w/c - v/c + wv/c2
+ w/c - wv/c2 + v/c - wv/c2
1 - w/c - v/c + wv/c2
=
1 - wv/c2
1 - w/c - v/c + wv/c2
t/τ'
= c2
- wv =
1 - wv/c2
(c - w)(c - v)
(1 - w/c)(1 - v/c)
Similar,
but not gamma. Not surprising, since gamma only has
one velocity variable. But in Einstein's derivation of gamma,
regarding x and t, he already had two velocities. His set-up for
the addition of velocity section is exactly the same as his
set-up for x and t, in the first section. The only difference is
he had a light ray moving—as his second velocity—in the first
part, and a point in the second part. But in both sections he is
seeking equations for two degrees of relativity.
So what if we substitute the speed of light for w in the last
equation above? Does it then resolve to gamma?
t/τ' = (c2 - cv)/ c2
- c2 - cv + cv
No, it resolves to infinity,
just like Einstein's t-transformation. What does Einstein's
addition of velocity equation resolve to if w is replaced by c?
V = w + v
= c + v
= c(c + v)
= c
1 + wv/c 2
1 + v/c
c + v
V resolves
to c, in that case. The velocity of light is c whether it is
measured from k or K. That is Principle 2 again. But then that
means that Einstein's adding and subtracting of v from it in the
tau expansion was pointless. My final equation for V also
resolves to c if w is c, but I did not get there like he
did.
Now, you may say, why not use "equation 5"
above? It looks very much like Einstein's equation, except that
we are adding the velocities in the denominator rather than
multiplying them. At most speeds this would only be a small
correction to Einstein and would seem to imply that his math was
not that far off.
We can't
use that equation for one very important reason. The velocity
variables don't match Einstein's. Mine are prime, his were not.
Mine are the local velocities of k and the point. The other
reason not to use equation 5 is that in most real situations we
will not be given the local velocities. In using the relativity
equations on quanta, for instance, the givens are not local
velocities. We have no local knowledge of quanta. We would be
given relative, or measured-from-a-distance, numbers to begin
with, and would need an equation to determine the addition of
these numbers. The famous experiment of Fizeau (explained by
Einstein) is another example. We are given the speed of the
liquid. But this is our determination of the speed of the liquid,
not the liquid's. The given is not a local measurement of the
system.
Please notice that my
new equation for the addition of velocities gives us numbers that
are very close to Einstein's in most situations. It differs from
his in having another easily comprehensible term in the numerator
and a minus sign instead of a plus sign in the denominator. But
it may be used with confidence, since it has been derived from a
thoroughly analyzed situation, as above, from five different
co-ordinate systems. My first-degree equation for velocity also
gives us a fraction more slowing at the speed of a space
satellite, which answers the Jet Propulsion Lab's decades-old
problem.
1"On the Electrodynamics of
Moving Bodies", Annalen der Physik, 17, 1905.
2"On
the Electrodynamics of Moving Bodies", Annalen der
Physik, 17, 1905, p. 8.
3Relativity,
Ch.XII, last page.
4 Historical Note: Max Born
used gamma without the square root, perhaps for this
reason. But this does not address the other substitution errors I
have shown.
go
to homepage
go to chapter 6
Links
To
read an exchange of emails with well-known physicists and
mathematicians on the operational measure of time, and on the t
variable in the Lorentz transformation equations of special
relativity click
here.
If this paper
was useful to you in any way, please consider donating a dollar
(or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me
to continue writing these "unpublishable" things. Don't
be confused by paying Melisa Smith--that is just one of my many
noms de plume. If you are a Paypal user, there is no fee;
so it might be worth your while to become one. Otherwise they
will rob us 33 cents for each transaction.
|