return to homepage
The Perihelion Precession First posted July 1, 2007
In 1859 LeVerrier did a extended classical solution of the problem of Mercury's precession. This solution showed that Newton’s and Kepler's equations fell short of the empirical data by a margin that could not be assigned to instrument failure or other error. This margin—38 seconds then, 45 second in Einstein’s time, and now 43 seconds of arc per century—became the holy grail of a thousand theories. Some like LeVerrier searched for another perturbing body in the region of the Sun to explain the discrepancy—a hidden moon of Mercury or a tiny inner planet.1 Others hypothesized various new gravitational potentials that would explain the number. Oppenheim published a review of these new theories in 1895, but none of them contained a convincing mechanism for the new potential or field. Soon thereafter, Paul Gerber published a paper that offered another ad hoc theory that would explain the precession of Mercury by proposing a field constant, but since this constant also had no mechanism or explanation, the theory made no impact (until it was dredged up by anti-Relativists 18 years later). After 1907 several physicists and mathematicians began applying a curved field to the problem in order to solve it, including Nordstrom, Klein, Hilbert, and Einstein. Nordstrom was the first to offer a full solution in this manner, but the solution was seen to fail in several ways. Einstein’s first solution also failed, achieving less than half the needed margin (it was thought). But by working with Hilbert and others, Einstein was able to get his total up to 45 arc seconds, and the solution was thought to be in hand. Hilbert actually beat Einstein into print with the same field equations, but since he had used Einstein's postulates he was forced to retreat, and the laurels went to Einstein.
Now for the second part of my critique. The entire analysis above assumes that GR is at least correct in principle, and that the historical analysis is at least correct in principle. All I do is show that both were misused. I leave upon the possibility that GR could be applied to the problem in a complete and logical way, and that if it were, the correct total might be achieved, though in a different way than we have been told. For instance, even admitting all my points above, it is possible that the number 43 is correct, it is possible the given total is correct, and it is possible that we can achieve that total by raising the perturbation total and lowering the equinox total, or something like that.
Here I will apply my simplified equations and dynamics to Mercury's orbit and see if I get the number 45. As you will remember from my simple solution to starlight deflection, I solved by taking Einstein's principle of equivalence literally. That is, to create a rectilinear field, I flipped all gravitational acceleration vectors, allowing the material bodies to expand.4 What we will be looking at here is the light travelling from the Sun to Mercury. Since the Sun would be expanding after the emission of the light, we may disregard it. We need look only at the expansion of Mercury while the sunlight is in transit. Now let us move on and look at precession due to perturbations. Even if we accepted the figure of 528 (and we don’t), we must see that the historical analysis, including that of Einstein, is very incomplete. If we go to Wiki today we learn that the Earth has a precession of its perihelion just like Mercury, and that this precession is also thought to be caused by perturbations from other planets. It is called the anomalistic precession of the Earth. Mysteriously, this precession is never included in the analysis of Mercury, although clearly it must affect our measurement of Mercury's total precession. If the Earth and Mercury are both precessing due to perturbations (and we assume they are precessing in the same direction, since both orbits are prograde) then one number has to be subtracted from the other in order to get a resultant precession. To me this seems obvious, but so far it has been ignored by everyone. The given number for anomalistic precession of the Earth is 1157, a number I will take on faith here since it comes from observation, not calculation. Here are the numbers we had before the perturbation correction:
Now for the final analysis. Some will ask how my corrections affect Earth's own precession, so let us look at the numbers again, disregarding Mercury completely. My corrections have to make sense with the Earth alone, as well as with the Mercury/Earth problem.
*Felix Klein and David Hilbert both worked with Einstein on his math, so they are the first to blame. The fact that they either contributed to these errors or utterly failed to notice them is reason enough for the lack of respect I appear to have shown them in other papers. If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.
return to updates
of Mercury
Go to gloss of this paper
by Miles Mathis
The title of my ongoing book is The Greatest Standing Errors in Physics and Mathematics, and the problem addressed in this paper certainly qualifies. It took me a while to get around to a full analysis of Mercury's orbit, but now that I have done so I have managed to surprise even myself by the sheer number of errors I have uncovered—and I am not easily surprised by errors anymore. But the quality as well as the quantity of these errors is enough to impress anyone, as I hope you will agree by the end. I say quality, because the magnitude of these errors may be even more surprising than their number. As I will show, the most basic rules of math and logic have been flagrantly ignored in full view of history, and not one person has deigned to notice in almost a century.
General Relativity is probably the most famous physical and mathematical theory in history and it has been combed and extolled by all the most famous figures of the 20th century. Which makes it almost impossible to believe that it contains flaws that are so elementary. These are not flaws embedded in difficult manipulations of the tensor calculus or in difficult motions of curved space, they are flaws of simple reasoning and number assignment. As an example and teaser, Einstein assigns his famous number .45 to precession per year while having no mathematical or theoretical reasons for that time assignment. By checking all his famous papers on GR, we find that he certainly found the number .45, but we find nothing in his equations that makes that per year. He simply assumed the period of precession, since his number matched historical equations. As I show, this assumption was false, since his number .45 applied to the curvature of his field at the distance of Mercury's orbit. That is, it was a constant, applying during one second or one century. He needed more math in order to apply that curvature to the precession problem, but he never did that math. He simply applied the curvature number directly to precession. This is not only mathematically disallowed, it is gloriously negligent. I don’t know—and probably no one knows or ever did know—whether this was an oversight or a purposeful fudge. It may be that he couldn’t see how to get from the curvature to the precession, so he just took what he had and ran with it. Because his audience was already monumentally confused, no one noticed.
As it turns out, he applied the curvature per year to the Earth year: that is, .45 per 365 days. He did that because it would mean .45 is what we on Earth would see. It would immediately confirm the number. Unfortunately, the curvature must be applied to the Mercury year of 88 days, since the curvature is applied to the orbit of Mercury! And this means Einstein needed to transform 88 days to 365 days, to explain the .45 we see from the Earth. But he didn't want to do that, because it would change the number .45 and ruin his math.
As I will show, the curvature is indeed about .45; but the precession (or curvature per Earth year) is almost twice that. Since Einstein desperately needed .45 and had been working on it for years, he purposefully ignored the last step. Everyone was looking for the number .45. They weren’t looking for another number. Another number would require redefining the whole problem, and no one wanted that. A solution in a certain form had been expected for years, and Einstein decided to give them that.
This mistake was just one in a long series. In this paper I will show that the entire historical analysis of the precession of the perihelion of Mercury has been riddled with basic logical and mathematical errors. I find this not only shocking to consider but also painful to report since the central character here is once again Einstein, a scientist I admire and like in many ways. I admire his stance against the Copenhagen interpretation. I like his humility in regard to 20th century science (about which he said, "If I have learned anything from a long life’s ponderings it is that we are much further from a deeper insight into the elementary processes than most of our contemporaries believe, so that noisy celebrations are not much in line the the real state of affairs."—compared to the horn tooting we get now from all quarters, this is highly refreshing). And I admire the brash synthesizing he did in his early years, collecting data from all over and forcing it into a semi-viable theory. Without his self-confidence, both Relativity and Quantum physics might never have gotten off the blocks.
In many other papers, I have also defended the basic postulates of SR and GR, so this paper cannot be seen as a fundamental attack on Relativity. Everyone who has read my papers knows that I am not an anti-Relativist of any sort. I have spent a great deal of time correcting Einstein's math, but these corrections only make Relativity stronger. Time dilation, mass increase, gravity-acceleration equivalence, the constancy of the speed of light from all systems: these all must stand. There is no return to Newton. Which makes it all the more difficult for me to say that Einstein failed to follow the simplest procedural rules for problem-solving regarding Mercury’s perihelion.
The only mitigating fact in his favor is that no one else followed these rules either.* None of his contemporaries or precursors followed any basic rules of logic in trying to solve the problem, none of them seriously questioned his findings (based on these flaws), and no one since has launched a serious critique against GR based on the way it was applied to this problem. The entire set of logical and mathematical anomalies I will relate has passed unremarked for almost a century.
This paper is divided into three parts. In the first part I will give a historical overview of the problem and then show the first central mathematical and procedural errors. These errors are led by the error of using Newton’s equations to define a gap between math and data, and then using new field equations to fill that gap. I will show that this procedural error infests the problem to this day, and falsifies almost every number we now take as a given.
In the second part I will show the second series of errors, which are kinematic in nature. Some would consider these to be metaphysical, I know, but they are not. I show that Einstein's kinematics and dynamics contain the same problems as Newton's, and then some. I consider force at a distance problems as well as field assignment problems—the major problem being that Einstein's influences and waves travel as mathematical abstractions but interact with mass as physical objects.
In part three I apply my simplified Euclidean field equations—the ones I used to solve the deflection of starlight in five lines—to the orbit of Mercury. Those who detest theory and groundwork, and who are only interested in equations, may want to skip directly to part three. I admit that this is where the real hard evidence is in this critique, and I only put it in the third part because I know that many or most readers will need an introduction to the problem and a rather lengthy explanation of all that is involved. It is probable that even this long paper won’t have the space to explain everything involved, and all but my most die-hard readers will have to take the links and see what I have already proved regarding GR and SR in other papers. Even those who rush ahead to the end of the story here would be better advised to read the paper as I write it, since nothing I say here is superfluous. The progression of argument is necessary or I wouldn’t have used it.
At any rate, in a very direct manner I am able to derive the curvature of the field, finding the angle with just a few lines of simple math. My number is again the same as Einstein's. But I show precisely what this angle represents, and why the number .45 cannot be "per year." I then show the correct math to discover a per-year precession due to curvature, proving that Einstein completely and mysteriously skipped this necessary step. I show that this number is not .45 or .43, and that the GR field therefore does not fill the historical gap as it has been thought to. I show that we must recalculate the perturbation numbers, for a start. After that I show that we must do a vector analysis on all the various types of precession, both on the Earth and Mercury, paying close attention to direction. I then conclude.
Part 1
It is now said that Einstein predicted the margin, which is one reason why General Relativity is so famous. But this is the first of many falsehoods. As I have shown, the necessary margin had been known since the time of LeVerrier, and Einstein had several chances to make his equations match the data. So there was no prediction involved with Mercury. The real reason GR was such a smashing success is that Einstein was able to get his math to match both the perihelion problem and the bending of starlight by the Sun problem. No one else had been able to do that. Corrections to the field equations that raised the precession figure from 18 arc seconds to 45 also raised the bending figure from .85 to 1.7 arc seconds. When Eddington confirmed the second figure, Einstein was immediately world famous.
But that is the second falsehood. In 1919 Einstein's prediction for bending had been non-confirmed by the astromomer William Wallace Campbell, a respected figure. Charles Edward St. John, working out of the Mount Wilson Solar Observatory, failed to confirm Einstein's redshift prediction at about the same time. So it is astonishing that Eddington’s confirmation was accepted with no other corroboration, especially considering the state of his proof. Eddington had two sets of photos from two widely separated expeditions, one in Principe and one in Sobral, Brazil. The main plates from Sobral strongly indicated the Newtonian value of .85, and so were failures of GR. The plate from Principe was difficult to measure and so had a margin of error stated to be from .9—1.8. Yes, you read that right: plate, singular. Due to persistent cloud cover, Eddington got only one useful image from Principe. And on this plate, a deviation of one second of arc represented no more than 1/60th of a millimeter, so Eddington had to use a micrometer placed directly on the plate. Eddington admitted a large margin of error, but the real margin of error was so great that the plate was experimentally useless—especially as it had to stand on its own.
Considering everything, I think it is astonishing that Eddington's conclusions were accepted with so little argument. Eddington dismissed his main plates from Sobral, taken with a large astrograph, claiming that the pictures had been distorted by overheating of the heliostat—although this distortion was never unambiguously confirmed. Instead, he used seven "auxiliary" photos, taken in Sobral using a 10cm telescope with a converted measuring instrument, to back up his one plate from Principe. The measurement of these auxiliary photos mysteriously took months, but at the end they were said to confirm "with absolute unambiguity and great accuracy." Whether they confirm or not is still up for debate, but in no case do they confirm either accurately or unambiguously. How could such a small telescope accurately confirm 1.7 arc-secs? If a 10cm telescope could confirm either unambiguously or accurately, there would have been no reason to bring along the large astrograph to Sobral, or to use a bigger lens in Principe. Even more astonishing is the fact that Eddington's findings were never confirmed by direct astronomical observation, and have not been confirmed to this day.2
Despite this, I treat Einstein's prediction for the Sun as confirmed [for the most part—to see my corrections go to my paper on Aberration], but not by Eddington, radio telescopes, pulsars, or other methods. I treat it as confirmed since it matches my own numbers achieved in a much more direct manner. As I have shown, Einstein's theory of equivalence—interpreted in a literal manner—by itself gives us the number 1.7, without using curved fields or the tensor calculus. My equations, which are a simplified and perfected form of General Relativity, also gave me the deflection figures for the outer planets, which I have confirmed using my own simple astronomical devices, as I show in another paper. Although these do not confirm Einstein's numbers for the planets (my number for Jupiter is very different from Einstein's), they do confirm the main postulates of GR, such as equivalence, and the postulates of SR, such as time dilation and light constancy.
Having confirmed Einstein's number for Solar deflection of starlight, I then went to the problem of Mercury's orbit, to see if his field equations achieved the right number there. Unfortunately, I found nothing of the sort. His equations yielded the same number as mine for curvature of the field, but not for the precession, since the two phenomena are not the same. Einstein applied the curvature number directly to the per-year precession, but I show incontestably that this is not possible.
The first thing I discovered is that the problem of Mercury is much more complex than Solar deflection, both historically and mathematically. Historically, there was very little lead-in to the Solar deflection problem. Eddington used Newton’s field to come up with a "Newtonian" number [.85] for the deflection, but this was seen only as a benchmark. It did not come directly from Newton, it had no longstanding historical pedigree, and it was not even accepted as standard by many physicists of the time (or now). Therefore, Einstein's prediction for Solar deflection existed in a sort of scientific vacuum. It had very little historical or mathematical competition, its context was not well understood, and there was no firm number for Einstein to match.
But with Mercury there was both a firm number to match and a history to account for. Lots of empirical data existed and had existed for a long time, and this data all pointed in one direction. In this case, Einstein did not choose to go in any other direction. He went where the data pointed and found the number that everyone wanted to find.
Mathematically, the problem of Mercury is also much more complex, since in this case the mechanics is not at all straightforward or transparent. The problem of Solar deflection is simple, since using either Einstein's method or mine, you encounter only one event or motion or force. But in the case of Mercury, the possible causes are many. Even if you accept the historical analysis, these causes form a long list, as I will show.
Finally, the problem of precession is much more complex than Einstein allowed. GR seems plenty complex, but most of that is due to the tensor calculus. Einstein's analysis of the motions and events is actually very incomplete, and it has never been completed since. A few minor updates to GR have come about in the past half century, but these are mostly mathematical variations on the tensor field, and they do not fill in the many large gaps that I will reveal here.
In this paper, the first pillar in my critique against Einstein comes from the historical overview I have already related. LeVerrier's basic equations are still accepted to this day (as corrected by Newcomb), and they are used to show how Einstein's field equations fill the historical gap. I will take my numbers from Wikipedia, since I like to show how Wikipedia acts as the mouthpiece of the status quo, but this break-down is the common one whenever the precession of Mercury is being explained. There is absolutely nothing non-standard about Wiki's theory. We know from observation that Mercury has about 5600 arcsec of precession per century, and we have known it for a long time. Just as LeVerrier told us 150 years ago, about 5029 of that is due to precession of the equinoxes—a terrestrial phenomenon in the first instance. About 528 of that is due to gravitational perturbations from other planets, mainly Venus. That leaves 43 unaccounted for. Wiki gives .02 to Solar oblateness or quadrupole moment, but I won’t address that here. 42.98 ± .04 is given to General Relativity.
It is in this list that the logical fault became apparent to me. Only the number 43 comes from GR. The rest of the numbers come from Newton. Einstein has filled a Newtonian hole with GR dirt.
Let me put it another way. The entire reason that Mercury's perihelion precession was still a problem in 1900 is that Newton's equations couldn't solve it. But if Newton's equations can't solve the last 43 arc secs of the problem, then they can't solve the first 5557 arc secs either. If Newton's equations fail, then they fail from beginning to end; they fail in every part of the problem, not just in the gap.
To show this more clearly, let us say I have a theory about how to measure the length of my desk. This theory supplies me with equations. Using these equations, I find the number x centimeters for the length of my desk. I now measure my desk and find that my desk is actually x + 4 centimeters. My equations have failed. Logically, this means that I must come up with a new set of equations. I can’t come up with a second set of equations that applies only to the gap of 4 centimeters, continuing to use my old equations for the rest.
But this is precisely what Einstein did. He allowed the failed equations of Newton to define the gap, then used a new net of equations to fill the gap. There is no other way to describe that, except gloriously bad math and logic. This gloriously bad math and logic belongs to everyone in past 150 years, not just Einstein, since everyone accepted this procedure (and still does).
It is clear that the form of the problem, at least as it was understood at the time, required Einstein to apply his field equations to all the bodies thought to be involved in the mechanics of the precession. This means he needed to apply the field equations to all the planets that were perturbing Mercury. But he never did this. He never even applied his equations to Venus. And, as I will show, he didn't apply them to the Earth either. The number 45 comes not from re-calibrating all the planetary perturbations, it comes from redefining Mercury's own orbit. Einstein applied his field equations to Mercury's orbit only, finding 45 seconds of arc caused by the Sun's curvature of the main field. In form, this was like Newton’s own efforts to show precession using the main gravitational field alone. But Newton had failed to get the right numbers, whereas Einstein was thought to have succeeded.
But Einstein cannot have succeeded, since the number 45 applies to the orbit before planetary perturbations. And to get the right total, Einstein used Newton's own equations for the perturbations. The only way this can work is by some major fudging, since planetary perturbations cannot be unaffected by a total redefinition of all fields. It is completely illogical to assume that GR affects the isolated orbit of Mercury by 43 seconds, but somehow fails to affect the orbits and gravitational strengths of the other planets.
In fact, it is admitted now that GR affects all the orbits, and the field equations have since been used to explain other precessions and perturbations. But the problem I have pointed out has been swept under the rug. The standard model now implies (by omission) that GR applied to all perturbations on Mercury cancels out, giving us Newcomb's old numbers to within a close margin of error. But I ask again, IS THIS LIKELY?
For this to be the case, we would have to find that all the perturbations once again added to 528 arc secs/century. This could happen in only two ways: 1) GR provides no variance from Newton’s numbers, 2) some planets are affected positively and some are affected negatively, and the positive effects cancel the negative ones exactly. Concerning 1), I find the odds of this to be effectively zero. Just as a start, the orbit of Venus has to be affected by the same large curvature of the main field by the Sun as Mercury. The two changes by GR to the two orbits will be cumulative, and the change in perturbation will be a compound of the orbital changes and the effective mass changes. Remember that GR, like SR, will change the relative masses of the two planets, compared to Newton. With Newton, the two planets were thought to exist at the same time, in absolute space. With Einstein, we must remember that we are measuring their masses from two different distances. The masses we use in perturbation calculations are always measured from a distance, so that we never really measure either planet "now." We always see both planets some minutes in the past, and we rarely see them in the same past. We know the mass of Venus relative to the Earth, and the mass of Mercury relative to the Earth, but we have not yet calculated the mass of Venus relative to Mercury. According to Einstein, this is not a straightforward calculation, and we may not rely on Newton’s equations to achieve it. And this is just an initial analysis. I could go on for pages on just this facet of the problem. Concerning 2), since all planets and most moons travel in prograde orbits, it is difficult to see how GR is going to increase some perturbations and decrease others. Logically, given the mechanics of the Solar system, GR will either have to increase the total perturbation on Mercury or decrease it. No cancelling out of effects appears to be possible.
Part 2
But now I will have to deflate that possibility as well, I am afraid. If Paul Gerber's ad hoc field constant had to be dismissed because it had no mechanical foundation (see above), and if all of Oppenheim's collected theories of field potentials had to be dismissed for the same reason, then Newton's equations also have to be dismissed on that basis. And so do Einstein's. Everyone knows that Newton's gravitational force has no mechanical explanation. It has a non-mechanical explanation, that being force at a distance, but we say we don’t allow that kind of magic anymore. If we don’t allow that kind of magic, then why do we allow Einstein’s kind of magic? How does mass curve the field? Since the field is at a distance from the mass, we appear to have force at a distance again. Why is no one bothered by this? I suppose it is because they think the graviton will soon be discovered, but Einstein never proposed the graviton as the force-bearing particle of GR. Later he calculated that gravity waves might be caused by his field, and that gravitons might compose these waves, but he never proposed the graviton as the mediator of the fundamental field—especially not by simple bombardment. For Einstein the field was geometric, not dynamic, and modern apologists for Einstein concur: there are no forces, and the interactions are not mechanical in the way of Newton. But the only way to get around the force at a distance problem in GR is to propose that the field is composed of gravitons, and that the gravitons transfer force by direct contact. Anything short of that implies force at a distance or curvature as a non-mechanical phenomenon. Curvature is a non-mechanical phenomenon because Einstein never shows us the mechanics. Since he doesn’t show how mass curves space, we could just as easily claim that space is curved even without mass. His only answer to this is empirical: we find curvature in the vicinity of mass. But that is not mechanics. Newton could say the same: we find attractions only in the vicinity of masses, therefore the masses cause the attractions. It is probably true, in either case, but it is an existential explanation, not a mechanical one. Any fool can come up with an existential explanation. In physics, we want a physical explanation. Post hoc ergo propter hoc or iuxta hoc ergo propter hoc3 is not good enough.
Some will say that I have answered my own question: I complain that GR is not mechanical and they will reply, no, it is geometric. It therefore requires no mechanical explanation. But this is a transparent dodge. Even if I accept that space is no longer physical and that it is now a mathematical abstraction, I still may ask how matter curves the math. Einstein never denied that the Sun was physical. How does the Sun curve the mathematical field? Physicists now hide behind the math at every opportunity, pretending that mathematical fields can be postulated with no questions asked or allowed. If you want a curved field, you propose one, that is all. If someone asks you why it is curved, you claim that math is abstract and it can be anything we want: questions about math are disallowed. But this is absurd. Applied math is not pure, and it is not metaphysical to ask questions about application. Metaphysics or semantics has nothing to do with it. The question is definitional or operational or logical, and is fully allowed. To deny this is to claim that you may not ask physical questions about physics.
And this is not Einstein's only problem. Newton had one big hole in his dynamics, but Einstein has many. The second major hole can be seen in perturbation theory, where he has to explain distant forces without forces. His fields have no forces, remember. Motions are caused only by travelling field disruptions, in the form of curves. Unfortunately this leaves us with travelling waves that somehow do not mechanically influence eachother. The curvature of space affects masses in that space, but does not curve other curves. Curves moving through curved space do not become more curved. For instance, Venus can send a wave to Mercury, as a carrier of its perturbation, and this wave travels across and against a much larger wave receding from the Sun. Mysteriously, the Sun's wave does not tamp down the wave from Venus at all. It is as if Einstein's gravity field is not one field, but an infinite number of interpenetrating fields, where no curvature affects any other. If this is so, then it is like no other field we know. And it is certainly not mechanical. In any field mediated by particles, we would expect the particles to collide occasionally, creating interference. This cannot be so in the Solar system, since to explain the perturbations we see, we must assume non-interfering gravity waves. As I said in another paper, the Earth raises tides on the Moon, and the Moon raises tides on the Earth, which means the curve is curving both ways at the same time, with no interference. As with Newton, gravitational forces interpenetrate with zero resistance. Regarding the magic of Newton's force at a distance, this is no surprise; but given a mathematical field of curvature, or a field of gravitons, this is a grave contradiction.
This is clear regarding the graviton, I think, but it should be clear in the mathematical field by itself, even without the gravition. How can the curves affect mass if they cannot affect eachother? Some waves or particles can be imagined to pass eachother with little effect, like neutrinos, for example. But neutrinos also pass through matter with little effect. A gravity wave must affect matter—that is why it is proposed in the first place. It must either be substantial or insubstantial. If it is insubstantial enough stack infinitely with no interference, it cannot be substantial enough to move matter; and if it is substantial enough to move matter, it cannot be so transparent as to stack infinitely. Likewise, if gravity is thought of only as a mathematical curve, it cannot curve only in the presence of matter and uncurve in the presence of other curves. It either travels in the field or it does not. If it travels in the field as a curve, then it must curve the field. If it curves the field, then other curves moving through the same field must interact with it.
Einstein wants it both ways. He wants to get rid of space, having only the curves created by the math. This would mean that the curves define the interactions entirely. The curves are the mechanics. But then he wants the waves to act in unmechanical ways, as if they are only mathematical abstractions. No, it is even more than this, since even mathematical abstractions must affect eachother. Curves in mathematical space cannot pass eachother without effect, unless they are specifically defined in non-physical ways. Einstein wants to define his curves in non-physical ways and then imagine that they affect matter! So they travel as non-physical mathematical abstractions and then suddenly, in the presence of matter, they become highly interactive. GR has no logical or mechanical consistency. In fact, it has even less consistency than Newton’s classical field. This does not make Newton better; it makes both Newton and Einstein fatally wrong.
My theory of gravity solves all these problems directly, by proposing that every apparent force resolves to simple linear motion. There are no curves, no gravity waves, no gravitons, no attractions, no forces, no tensor calculus, no forces at a distance, no spooky forces, no paradoxes, no supraluminal speeds, no virtual particles, no Higgs bosons, no strings, and no non-mechanical ideas. Everything resolves to motion, even gravity, mass, and inertia.
Part 3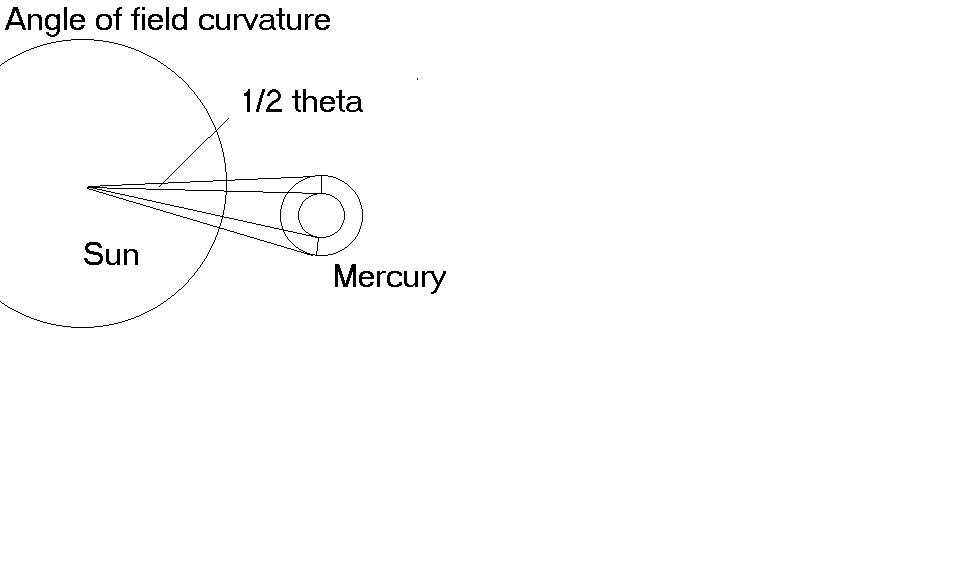
Let's start with the perihelion of Mercury, which is about 46 million km. Light travels that distance in 153.3s. The acceleration at the surface of Mercury is 3.74m/s2, so we find
s = (3.74m/s2)(153.3s)2/2 = 43.9km
Mercury expands that much in one direction while the light is travelling from the Sun to Mercury. But since Mercury is expanding spherically, we must double that number. The radius will expand 43.9, but the diameter will expand 87.8.
tanθ=87,800m/4.6x1010m
θ = .394 seconds of arc
This is interesting, since that is very near what LeVerrier initially found (see above). If we use mean orbital numbers, we get .49. And if we use the numbers Einstein used,5 we find θ = .45 seconds of arc.
No doubt you will have some questions about this. Einstein found .45 seconds of arc per year, whereas I seem to have found about .39 seconds of arc per 153s. But this is not how my equation works. My equation finds the same amount of precession no matter what time period you use. Whether you use 1s or one century, you still get .39 arcsec. This is because .39 arcsec is the curvature of the field. At a distance of 46 million km, the total curvature of the Sun’s field is .39 arcsec. That number applies to the angle at the Sun, not the precession directly. In my theory of expansion, I apply the angle to Mercury itself; but if I like I can flip the field 180o and apply it to the Sun—this is how I solve GR problems without the tensor calculus. I reverse the field.
Einstein's equations work the same way mine do, except in reverse. I give the curvature to the size/time plot and Einstein gives it to the vector field (where the curvature applies to lengths), but otherwise our math is doing the same thing. It not only gets the same number, it yields the same implied mechanics (in reverse). That is to say, Einstein's number is not only the same as mine, his assignment is the same as mine. If you check his math closely, you see that his curvature number is a field constant at a given orbital distance, and it has no possible time assignment in the first instance. It is not .45arcsec/s or .45 arcsec/yr, it is just .45 arcsec. Like mine, Einstein's math yields an angle, not an angle per time.
Whether or not you accept the full implications of my theory or my math, you must admit that .45 applies to the curvature. In fact, Einstein told us this himself. But if it is the curvature of the field, it can’t be applied directly to the precession. The curvature of the field is just an angle constant. It implies no time period. To find the time period we must analyze the problem more closely. Einstein did not do this.
If Einstein did not make sense of his number, how shall I proceed to make sense of mine? First of all we will not need the full curvature of Einstein’s field in order to find the precession. Precession is an orbital phenomenon, and an orbit is defined by motion in only one direction in the field. What I mean is that an orbit is either prograde or retrograde at each instant. Although the planet is expanding in all directions at once, its orbit is in only one of those directions over any small interval. Or, to put it in current terms, Einstein’s curvature applies +x and –x at the same time. The field curves both forward and backward and to both sides for a moving planet, so when I wanted to express that with my expansion field, I had to take the increase in the diameter, not just the radius. But since the planet is only moving in one direction at each moment in its orbit, its precession need only take account of half this curvature.
I am going to compare Mercury's field curvature or expansion to the Earth's later, so I am going to switch to an average orbital distance instead of the distance at perihelion. This is also necessary due to the fact that over the period of a year or century, Mercury will not always be at perihelion. We have to find an average over a long period of time, in order to solve this problem. Making the proper substitutions above, this makes our curvature estimate .245 arc sec (half of .49).
Now we need to compare Mercury's velocity due to curvature to its orbital velocity. This will give us precession per period of orbit. We have a number for acceleration, 3.74m/s2, which is just the gravitional strength of Mercury at its surface. We flip that vector and apply it to a real acceleration, a la Einstein's equivalence principle. Since we are taking half the curvature, we only need half the acceleration, and the acceleration will give us a velocity. That velocity is obviously v = at/2 = .936m/s. That is Mercury's velocity in any one direction due to either curvature or expansion. To turn our curvature number into a precession number, we must compare Mercury’s velocity due to acceleration to Mercury’s orbital velocity. This will give us the numerical relationship between Einstein’s field curvature and the orbit of Mercury.
Here we run into a problem that no one else has been able to solve, because no one before me saw it as a problem. That is, Einstein couldn’t have solved it if he had discovered it. In my paper on the equation a = v2/r, I proved that physics has forgotten a distinction that Newton was careful to make between orbital and tangential velocity. This is important here because you can see that we need to compare a straight-line velocity to a curved "velocity." The number .936m/s that I just derived is not an angular or orbital velocity. It describes the velocity of the surface of Mercury in any one direction. And although it is caused by curvature or expansion, it is not a curved vector. In my math, it is a straight-line vector. I don't have any curves in my math here, much less tensors. But now we need to compare it to Mercury's given orbital velocity, which the books tell us is about 47,000m/s. Problem is, an orbital velocity curves. The orbital velocity is 2πr/t, and it describes a circle, as we all know. So we can’t compare it directly to our expansion velocity. A so-called orbital velocity is a very convenient number since it gives us the distance and the time of one rotation. It is also very easy to see in data. But it is not really a velocity, since velocities do not curve, by definition. We need an equation—a sort of transform—that will give us a real velocity from this misnamed orbital velocity. Before I wrote my paper, you would look forever and not find this transform, since it did not exist. Even Newton did not give us a way to find it. The tangential velocity has been buried for hundreds of years. But we need it here, so it is fortunate I happen to be the one who knows how to find it. This is the equation we need here:
vt = √(a2 + 2ar)
To calculate this, we need the acceleration of the Sun’s field at the distance of Mercury, and that is easy to calculate with the numbers we already have.
a = v2/r = (4.7 x 1042 /(5.82 x 1010) = .0379m/s2
vt = 66,400m/s
Now we compare the two complete rotations, given the two velocities. If it takes 87.8 days going 66,400m/s, then it will take 6,220,000 days at .936m/s. That means it takes 6,220,000 days for an expanding Mercury to eat up its entire orbit by expanding into it, or a curving Mercury to eat up its orbit by extra curvature. Now to relate that to the number .245. There are about 5.3 million of those periods in one orbit (5.3 million times .245 equals 360 degrees). In other words, if we let Mercury expand as in our equation above 5.3 million times, it will create one full orbit. So now we have another equation:
(5.3 x 106 )(.245 arc secs) = 6,220,000 days
PM = 76 arc sec/yr
This may seem at first like a huge amount of precession, but remember that we never see this kind of precession from the Earth. As I will show, we must subtract the Earth's own precession due to curvature to achieve a usable figure, and we have never done this. If you look at all the glosses of Einstein's problem, including the latest updates, you will see that no one calculates the Earth's precession due to curvature. This is because they mistakenly think the number is negligible. They think that Einstein's 1.7 number applies only to the deflection of starlight and not to the Earth's field curvature.6 But, following Einstein, they have misunderstood the entire gravitational field and its mechanical causes. I will calculate the Earth’s curvature below and show that it gives us a number that fits the current data in all important ways.
To show that my new equations have not mirrored and corrected Einstein's by some sort of accident or coincidence, let us apply them now to the Earth. In a previous paper I showed that the total curvature of the field at the distance of the Earth's orbit is 3.36 arc secs. I achieved that this way:
s = at2/2 = [(9.78 m/s2)(501s)2]/2 = 1,230,000m
tanθ = 1,230,000m/1.51 x 1011m
θ = 1.68 seconds of arc
These equations I have simply imported from my paper on Solar deflection. This is my famous GR solution in three lines of math. It gives us the apparent bending of light from the Sun, as seen by an observer. It also gives us the angle of expansion in one direction. Doubling that represents expansion both prograde and retrograde and therefore stands for the curvature of the whole orbital field. Hence the number 3.36.
[To see why this number 1.68 does not match the current number 1.75, go here. I show that gamma causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.]
Now let us find the precession of the Earth due to this curvature or expansion. We will do it the same way we found Mercury's.
a = v2/r = (2.98 x 104)2 /(1.496 x 1011) = .005736m/s2
vt = √(a2 + 2ar) = 41,400m/s
(41,400m/s)(365 days) = (2.45m/s)(6,160,000 days)
(7.71 x 105 )(1.68 arc secs) = 6,160,000 days
PE = 76.8 arcsec/yr.
Now, if we subtract Mercury's precession from the Earth's, we achieve the apparent precession of Mercury as seen from the Earth. This is the number we want. This gives us a difference of
ΔP = .8 arcsec/yr
Or 80 arc secs per century. Therefore we will see Mercury precess about 80 arc seconds per century, due to curvature of the field alone. This is almost double Einstein's 43, which is enough to disprove his math and postulates. It also means that we will have to re-figure the perturbation total. The number 528 from above cannot be correct, as I said, since that is a Newtonian number, not a Relativistic number.
But first let us look at something very interesting. Now that we have a number for Mercury's precession due to curvature, we must return to our equations and consider what it means. Notice that if you divide 365 days (the Earth year) by 88 days (the Mercury year) you get 4.15. If we take our very first number for curvature, .39, take half to express only the curvature in one direction (for the orbital direction in space) and multiply by 4.15 we get .8/yr. That is what we just got by a rather involved calculation. That means that the first angle should have been applied to the Mercury year. We could have skipped all the long math and simply written,
s = (3.74m/s2)(153.3s)2/2 = 43.9km
tanθ=43,900m/4.6x1010m
θ = .197 seconds of arc
.197 arcsec/88 days = (.39 arcsec/88 days) x (365 days/1 yr)
= .8 arcsec/yr = 80 arcsec/century
So Einstein could have leapt to the conclusion he did, if he had used the right year and the right angle. He could have taken the angle and applied it to one full orbit of Mercury. His number should have been applied to the Mercury year. But his math gave him absolutely no reason to apply it to one full orbit of the Earth. He calculated the extra curvature of the Sun's field at the distance of Mercury, so what could the orbit of the Earth have to do with that? He also used the wrong angle. He doubled it. This is interesting because historically his first solution got around half the angle of his final solution. Remember that his first lecture on GR found .18 for the angle, as I said above. I have just calculated that it must be about .197. His initial math was better than his final math. For the precession problem, he doesn’t need the curvature of the field in both directions, he only needs the prograde curvature.
But how does my abbreviated solution work? How did we skip directly to this field differential of .8 arcsec/yr without considering all the Earth numbers? It works because once you compare the Earth's orbit to Mercury's you must achieve a relative number. What I mean is that simply by using the term 365/88 in our math, we have made the problem a relative one. We are comparing the two orbits, and in doing so we have left the "absolute" field of the Sun. The number we get at the end of the calculations must be Mercury relative to the Earth, not Mercury relative to the Sun.
When you import certain terms into equations, those equations bring with them certain assumptions or axioms. They also carry with them certain information. You cannot use them without bringing these axioms and information to bear on the math. The term 365/88 already contains a load of information about the relative motions of Mercury and the Earth, and simply by using it we achieve a final number that includes all that information. We do not have to write all the information as numbers in our equations: it is already implicitly included in the term 365/88. And so we achieve a relative number at the end (.8 arcsec/yr) which is the precession of Mercury relative to Earth's orbit, not the precession of Mercury relative to the Sun.
There is a second important point to hit before I move on to perturbations. Notice that the number of days (6,160,000) for a full precession for the Earth is almost the same as a full precession for Mercury (6,220,000). This is not a coincidence. In fact, it gives us a way to check our math above one more time. From the point of view of the Solar field itself, the precession period of both planets should be the same. Why? you may ask. Two reasons: 1) There is no time differential if you measure from the field itself. To put it another way, you don’t have to do an SR transform if you measure from the field. Time differentials and Relativity transforms only apply if you are measuring one motion in the field from another point of motion. You will see what I mean by this in a moment. 2) Expansion is the same for all objects. That is why all objects stay the same relative size, and why we don’t see expansion. If the rate of expansion weren't the same, we would see Mercury changing size. We don’t see that, so the expansion must be equal. Not numerically equal, since 3.7 does not equal 9.8; but relatively equal. We have a variable acceleration here, and the variation is the same. In other words, the rate of change of the two accelerations is equivalent. If this is so regarding expansion, then if we flip the field back over to get Einstein’s curved field, it means that the curvature of the field is the same at both distances.
What I mean by that is, another of Einstein's major errors is that he thought the curvature of the field and the field strength were the same thing, but they aren't. The field strength determines the size of the centripetal acceleration vector from the Sun at each distance—.038 for Mercury and .0057 for the Earth, for example. But the curvature that he found with his tensor equations is the change in this field. It is the field variation. That is why it was an addition to the field of Newton. Newton already knew about the field strength of the Sun, and its variation with distance from the Sun. Einstein's equations don't apply to that (although Einstein thought they were just a simple addition to that field). Einstein's equations apply to the change in that field. Newton’s accelerations are rates of change of velocities, and Einstein's GR accelerations are rates of changes of accelerations.
It turns out that the rate of change of acceleration is the same for all planets. If we look at expansion, then all the planets expand at the same rate. If we look at curvature instead (as the inverse of expansion) then we find that the curvature is also the same for all the planets. To a first approximation, Einstein should find the same angle for each planet, since they are all part of the same variable field. He doesn't, and that is a major error. He thought (and physicists still think) that the curvature of the main field is less for the Earth than for Mercury. But it isn’t. The only variation comes from the time differential.
Some will say, if your argument is true, it means that the Earth and Mercury should orbit at the same rate. If the curvature is the same, the orbits should be analogous. But those who say this are missing the distinction I just made. The rate of orbit is not caused by the differential or variable field I just described. To a first approximation, the rate of orbit is caused by the planet's "innate" tangential velocity and the Sun's centripetal acceleration at that orbital distance, just as Newton told us. That is the main acceleration or gravitational field. It is a field of acceleration vectors or tensors. But the extra curvature field of Einstein is a differential field: it is the change in acceleration field, due to Relativity. That is why it is an addition to Newton. Einstein's .43 angle for Mercury is part of that differential field, and that is why it is not part of Newton's main analysis. It is a relativistic field, caused by time differentials, as I have shown and will show again in a moment. The precessions and forces caused by that field are only apparent. They are the outcome of time differentials.
This means that we have a field that is curved in two separate ways, although Einstein never saw this. Every rate of change implies a curvature, whether we want to use a curved mathematical field to represent it or not. I prefer to straighten out all the curves in my math, since the math becomes a lot easier and more transparent, but Einstein was correct in a sense when he showed that accelerations imply curvatures. Unfortunately, he conflated two rates of change. He tried to express Newton’s gravitational acceleration field as a curvature, which is valid. Accelerations can certainly be expressed mathematically as curves, if one desires. But the variation from Newton is not caused by representing the field as curved, in the first instance. It is caused by adding another curvature to that curvature, and the second curvature is caused by time differentials. That is, it is caused by Relativity. It is caused by the fact that Mercury is separated from the Earth by 499s, and that time cannot be ignored. This time differential creates another rate of change to the field, and that rate has to be added to the curvature of the main gravitational field. So we have two curvatures on top of eachother. One is SR, caused by time, one is GR, caused by gravitational accelerations.
Einstein never saw this, and no one since him has seen it. He was never clear on what his curvature was expressing. Because he never clearly separated his two mechanisms, his curved field became confused. He wasn't able to separate out all the events like I do, and his tensors soon became unassignable. Were they expressing the first curvature, the second curvature, or a combination? Often, no one could say. The math was too complex for anyone to really wield. And we now must add to this his basic ignorance of the correct vector analysis, as I will show. True, his tensors acted like complex vectors, but because he couldn't visualize all the interactions, he couldn't say when these vectors or tensors should be added and when subtracted. As I will soon prove beyond any doubt, it is of ultimate importance to your final numbers to know whether your apparent forces or differentials will be prograde or retrograde, and to know this you can't just throw math at the field. You have to intimately understand the field.
Let me do a bit more math, and you will see what I mean. The first math I did in this paper was a giant simplification and correction to GR, although it may have seemed difficult to some. The second math I did was even simpler. Now I will simplify even further.
We already know that there is an absolute time separation between Mercury and the Earth of 499 seconds. This is no bold claim of mine, it is current wisdom. The mean distance between the two planets is 1AU, and light takes 499 seconds to travel that distance. Therefore, all our measurements on Mercury are 499 seconds old. All our photos from Earth are 499 seconds old.
Given that, if Mercury is expanding at 3.7m/s, then it will have continued expanding while we were waiting for the light to get here with our information. Therefore, if we want to compare Mercury now to Earth now, we have to do a Relativity transform. That transform is very simple, given expansion, and we don’t need tensors. We just go back to our first equation and change the time. We let Mercury expand for 499s instead of 153s.
s = (3.7m/s2)(499s)2/2 = 460,600m
That tells us how much Mercury has expanded while we are waiting for the light to get here. Now, if we want to relate that to how we see Mercury's orbit or its precession, we have to divide by two, since once again we are only considering motion in one direction in the field. We are only concerned with half the curvature of the field, since Mercury's orbital motion is +x but not also –x. Now we just do the rest of the math:
tanθ=230,300m/5.8x1010m
θ = .82 seconds of arc
There it is again, the same number. Confirmation of our angle difference, without even looking at the numbers from the Earth. All we have to do is calculate how much the numbers change between Mercury and the Earth, and we do so by looking at how much light skews the problem directly. That is what Relativity is, whether we are talking about SR or GR. SR is how much the speed of light skews non-acceleration problems, and GR is how much the speed of light skews acceleration problems. Einstein assumed that GR couldn’t be solved in straight-line geometrics, but I have shown that it can. Basically, I have solved GR using SR directly. Using the postulate of expansion, all problems become SR problems, and I can calculate by simply looking at time differentials caused by light, in a straight line.
[A very clever person will say, "Wait, you just assumed that was .82 arcsec/yr, whereas you spent any amount of time complaining that Einstein made a per-year assignment in the same way without justification. What could possibly be your justification?" The answer is in the time used in the equations. I use 499s, which is connected to 1AU, which is the average distance of Mercury from the Earth. To get that average, you have to take positions over a full orbit of both bodies, and both bodies are moving relative to the field and the zero-point. The number we get at the end, 499, is therefore an average relative to the bodies in motion, and to their motion. It is a relative number: it is one orbit relative to the other.
Another way to look at it is that .82, although it is an angle to the Sun, is an angle as seen from the Earth, not from the Sun. The number is based on the time of 499s, and the Sun or the field itself never experiences that 499s gap. That light gap is between Mercury and the Earth only, so only the Earth sees the angle .82. It is a relative angle, not an absolute angle. It is an angle relative to bodies moving in the field, not an angle relative to the zero-point or the Sun. The time period is the year, since both orbits are defined by the year, and the time in the equation was taken from an average over an Earth year.
Perhaps a simpler way to put it is that since 499s is an average time over one full orbit, .82 is an average angle over one full orbit. If we did the full analysis, without averaging, we would have to take into account the fact that at some points in the two relative orbits Mercury appears to move forward from the Earth and at other points it appears to move backward (and at two point it appears to stand still). The angle at nearest approach would be .37 and at farthest it would be 3.0 (and in two points it would be 0.0). 3.37 divided by 4 is equal to .84, so you see that we have a good estimate just from those four points in the orbit. Once I actually average, you can see precisely how the number .82 is connected to the full orbit and the year.
The clever person will now say, "If it is an average over a year, then it will be an average over a century as well, won’t it?" No, it won’t. That sort of reasoning would work with linear averaging, but that isn’t the sort of averaging I am doing here, as you can see if you study the mechanics. In orbital motion, a residual angle after one rotation must be given to the precession after that one rotation. That is what precession is. One rotation is one year, in this part of the problem, therefore at the end of each year we collect the average angle and give it to precession. The next year we must collect the same angle again, or another angle if the mechanics changes.]
We should therefore simply subtract 528 from 1157, to get 629. But even that won't cover all the necessary corrections, since 528 can't be right. It can't be right for logical reasons, as I said above. GR must affect that number. But no one has ever done a comprehensive GR correction to the number, or if they have they have fudged it to keep Einstein's figure right. Since I have shown that Einstein’s math is completely compromised, we can now return to this number and look at it afresh.
The fundamental change that Relativity brought to all the classical fields is the concept of time as a distance measurement. That is why the time variable was brought into four-dimensional math as an equal partner, why Minkowski proposed symmetry, why the matrices handle time as just another field vector or tensor, and why the motion of light is now considered a measure of both time and distance. But what this entails for the gravitational field is mainly a weakening of all perturbations. This change is generally tiny, but it increases with increasing distance. The primary reason is that distance now affects both distance and time, whereas with Newton it did not affect time. This gives the field a sort of double drop-off where it only had a single drop-off before. This being so, the number 528 must fall. The number 1157 will not fall since it is an outcome of measurement, not calculation. That number comes from visual data, not from GR field equations. Therefore we know it is correct (in some sense). We only have to make our GR equations match it. But the number 528, being data that belongs to Mercury, is not visual data for us. It is calculated. And it must now be recalculated down using either Einsteins field equations or mine.
Is it possible to use the numbers we have so far to estimate a correction to perturbations, without looking at all the classical numbers? Mercury’s perturbation total is just the sum of all its solar system influences, so if we could get a percentage change due to GR on just one of those influences, we could use that percent to estimate a total change. We already have a considerable amount of new information regarding how Mercury is measured from the Earth, and that information should help us calculate a percentage change in the perturbation from the Earth.
A perturbation is simply a force transmitted from one body to the other. It could be transmitted in any number of ways. Historically, precession theory has assumed that the perturbation is gravitational, but it could be an electromagnetic force or any other force. No matter how caused, we would have to include it if it affects precession. To simplify this calculation, let us imagine that the perturbation from the Earth to Mercury is caused by the emission of one large moon by the Earth. The force will then just be the mass and velocity of this moon when it hits Mercury. We won’t concern ourselves with the question of whether the Earth is diminished by this moon or whether Mercury is augmented by it; we use the idea only to simplify the calculation. Let us say that according to Newtonian math, the force of this moon as it hits Mercury is 1 million N, and that the direction of the force is at a tangent to the orbit. This is about as simple as we can make it. The question is, how will GR affect the measurement of this force?
I have shown that the simplest way to solve these problems is by using expansion and the time differential. That gives us both variations or curvatures without giving us a curved field, and we can solve without tensors. The average distance of Mercury from the Earth is 1AU, but since Mercury must be at a tangent for our problem, we must do a tiny bit of math.
1AU2 = 58 mil2 + x2
x = 138 mil km
That is the distance of Mercury at the tangent. Light travels that far in 460s, so that is our time differential. If we use expansion to stand for curvature, then in that time Mercury’s radius will increase in size this much:
s = (3.74m/s2)(460s)2/2 = 396,000m
If Mercury’s relative density remains constant, then its mass must increase with its radius.
Density = mass/volume
5,427 = x/(4/3)π(2,440,000 + 396,000)3
x = 5.185 x 1023 kg
This means that Mercury's mass has increased 1.57 times while the radiation was in transit (assuming our moon can travel the speed of light).
But what has happened to our force? Hasn’t the moon gotten bigger, too? Rather than ask the question that way, we will ask what happened to each Newton of force, since this question better follows the math we are trying to update. A Newton is defined as a kilogram meter/s2. We will assume that the kilogram and the meter and the second will all expand just like Mercury did, so that our universe will remain visually consistent. But what will skew the problem is that the meter and the kilogram and the second don't expand in the same way. The meter and the second do, since they basically measuring the same thing, but you can see from the calculations above that the mass and the length don’t expand in the same way. As you see, Mercury's radius increased by a factor of 1.04, whereas its mass increased by a factor of 1.57. This means that one Newton will change this much relative to Mercury in 460s:
N = (1.57)(1.04)/(1.04)2 = 1.51
So, to sum up, the mass of Mercury increases by a factor of 1.57, but the force increases by a factor of 1.51. Therefore the resultant force must decrease by about 4%. Relativity gives us a 4% decrease in the perturbation.
If we assume that all the perturbations decrease by the same percentage, then Mercury’s total perturbation number of 528 will decrease to about 507.
You will say that my assumptions here are astonishing, but they are just the same as the assumptions of Einstein and Newton. All I do is reverse the field, which Einstein's equivalence allows. Newton defined gravitational acceleration in terms of mass, and I am just reversing his definition. I am defining mass in terms of gravitational acceleration, so that an increase in radius must give us an increase in mass, by definition. I turn all the vectors and definitions upside down, to see what they really mean for the math. Beyond that, my assumptions are just Relativity's postulates. Mass and length increase differently according to SR and GR, so I am not proposing anything new. I am just taking Einstein at his word. Even if you want to consider my method just a trick, like one of Minkowski's tricks, you have to admit it is quite a trick. If you don't admit it now, you will in a moment when I prove that 4% is exactly the right number.
[See end of this paper for links to later famous experiments which confirm my 4% correction to GR.]
Precession of the equinoxes: 5029
Precession due to curvature: 80
Precession due to perturbations: 1157 – 528 = 629
(Desired) Total: 5600
Remainder: 148
That doesn’t appear to work. But we must do a vector analysis. So far, all the historical analyses have simply added up the numbers. No one has appeared to notice that precession requires a vector analysis.
I remember when I first learned what precession was, long ago, I asked myself what the term meant: was it a relative motion forward or backward? I looked the term up in many places, but got no answer to this question. As it stands, the term is undefined in that regard. In astronomy, precession is simply relative orbital motion. We are not told if it is prograde or retrograde. There is no distinction of terms, like precession for retrograde orbital motion and procession for prograde orbital motion (although there should be). In fact, there seems to be some confusion in this regard, as if no one has yet noticed that there are two distinct possibilities.
Since precession due to curvature of the field (or expansion) is caused by matter usurping its own orbital circumference, this motion must appear retrograde. The planet must be further along than expected, but if the planet looks early, the orbit looks late. The orbit and the planet are not the same thing. [Since the planet is the primary visual object, we assume it cannot be early. It is where we see it (we think), so it is right on time, by definition. Which makes the orbit late, compared to the predictions of the math.] Also, I have shown that the Earth's precession caused by curvature or expansion is greater than Mercury's, which would make Mercury’s resultant motion prograde. If both planets are precessing retrograde, then the difference must be prograde, as a vector.
Likewise, the anomalistic year must be prograde in its main motion, since it is longer than the sidereal year. Mercury's anomalistic year (caused by most of the same perturbations) is also prograde, so the difference between the two will be retrograde.
Conversely, the precession of the equinoxes is retrograde, since the tropical year is shorter than the sidereal year. So let us relist the numbers with their correct signs.
Precession of the equinoxes: 5029
Precession due to curvature: -80
Precession due to perturbations: 1157 – 528 = 629
Desired total: 5600
Remainder: 22
That remainder is a beautiful thing to my eyes, since it is almost exactly 4% of 528. Watch this (I take the 507 from my perturbation correction above):
Precession of the equinoxes: 5029
Precession due to curvature: -80
Precession due to perturbations: 1157 – 507 = 650
Desired total: 5600
Remainder: 1
My proof is complete. I have corrected Einstein's field equations and applied them to the precession of Mercury. All my corrections resolve, and I have gotten the right answer to within less than 1 part in 5600.
Precession of the equinoxes: 5029
Precession due to curvature: 7680
Precession due to perturbations: 1157
How can I explain the extra number, since from observation we have no room for the additional 7680 arcsecs/century? That is a gigantic number that simply could not be missed. Well, it is quite easy, since we must once again do a vector analysis, not just an adding up of raw numbers.
Wiki tells us that, "Because the anomalistic year is longer than the sidereal year while the tropical year (which calendars attempt to track) is shorter, the two forms of precession add." That is true, if we measure both precessions relative to the tropical year. But if we measure the precessions relative to the sidereal year, it is false. Relative to the sidereal year, the two forms of precession subtract. Meaning, we need a difference. We have to use the sidereal year, because that is where we are getting all our numbers relative to Mercury. Mercury doesn't care anything about our tropical year, and the stars and Sun don't either. The tropical year is calculated using the ecliptic and equinoxes, but these things can be seen only from Earth. The fundamental field for measuring all sorts of precession must be the sidereal field. This being true, we have to subtract 1157 from 5029.
Precession of the equinoxes/perturbations: 3872
Precession due to curvature: 7680
Still doesn’t work, you say. Ah, but it does, since 3872 - 7680 = -3808. All the new number does is switch the direction of the precession. In this way we can incorporate the huge new number we found and still keep the number we have.
You can see that this is because we have another vector situation here, since as I showed above, equinox precession is retrograde. It is the bigger number, so the difference between equinox and anomalistic precession is also retrograde. But curvature precession is prograde in this case, since it is not a matter of what we are seeing, it is a matter of what we are doing. We are calculating our own precession, which we cannot see directly. Therefore the difference between planet and orbit does not apply. The only fact that matters in this case is that due to curvature or expansion, the Earth is eating up its own orbit, and therefore processing prograde.
Of course I would have liked for 7680 to be exactly double 3872, so that I could subtract and get exactly the same number I subtracted. This would have been beautiful, since the new vector analysis would then yield the numbers we already have. It would exactly confirm existing data. We didn’t get that, but we got very close. Even though my math here has just been approximations, I still got close enough to raise eyebrows.
I have heard some complain, regarding my papers, that I talk too much. Physicists and mathematicians are used to being fed just the equations, with very little or no explanation of what the equations are representing. But although I understand the complaint, I refuse to recognize it as valid. In my opinion, the slowness of progress in physics has been caused by this refusal of mathematicians and scientists to tell us what is going on. How else could Einstein’s major mistake in this problem have stood for so long? It is because he gave us no explanations with his equations. He skipped all or most of the procedural steps, and just supplied the bald derivation of the number. Yes, the use of the tensor calculus made the math quite lengthy, but the procedure was still but a skeleton. Einstein refused to lead us through his maze, so that we could see what was happening all along.
Some of my readers apparently would prefer I did like Einstein and the rest, and they imply that they can supply all the content themselves. But I don’t believe them. I don’t believe that they are able to follow complex physical problems abstractly any more than I can. In fact, they and everyone else has proved that they are completely incapable of just that. No one is able to elide over large parts of the procedures and mechanics and definitions and variable assignments, just following the math. We all need it on the table, so that we can go back and study each part: each equation, but also each assignment, each motion, each step, each definition, each postulate. The more that is brought out into the open, the more chance it will be criticized and corrected.
The physicists of the past and present are too secretive. All the papers I have read, from Euclid to Newton to Einstein to Feynman, have been like puzzles. They are criminally incomplete, and I can’t say that I fully enjoy filling all the omissions in myself. I am gratified in the instances I can do so, but I shouldn’t have to. Barebones math is not a physical solution to a problem. A solution includes the explanation of how the math works at all points. This sort of solution is correctable. Solutions like those of Newton and Einstein are not. That is one reason that both Newton and Einstein have had such longevity: no one could get behind the equations to pull them apart.
After breaking through both walls—those of both Einstein and Newton—I can tell you that this incompleteness appears to be purposeful. They, like most other scientists, have hidden the groundwork because they had no confidence in it. They kept it out of the light of day because it could not survive the light of day, and they knew it.
I am quite sure that I have made any number of mistakes in this paper, and I am aware that everything is right out in the open. But I prefer it that way. I am not confident that I am right about every number, or even about every procedure. But I am confident that I have pushed the problem well beyond where Einstein left it, and that is quite enough for me. If any one of my many points or suggestions here leads to a stronger theory of gravity, I will have done my part.
Update: October, 2009. This original paper was published in 2007, but in November of 2008, Lorenzo Iorio published an announcement with ArXiv7 that E.V. Pitjeva had analyzed Cassini spacecraft data, finding that the precession of Saturn did not conform to the predictions of GR. The gap between data and prediction was calculated to be .004-.008 arcsec/cy. The announcement in ArXiv corresponded to a paper by Iorio and Ruggiero in SRX Physics8 at about the same time, in which the authors showed that theories of long range modified gravity (LRMG) could not explain the gap. This was in preparation for a paper by Iorio in July, 20099, which proposed that an undiscovered planet X was causing the gap. This is a drole repeat of history, since in 1859 Le Verrier proposed the planet Vulcan as the solution to the original problem with Mercury. As you can now see, we need neither a new planet X nor any LRMG. The only modification we need to gravity is the simple one I have shown above. We don't need to "modify" gravity at all: we only need to correct the simple mistakes in the equations we have. In fact, my finding that Einstein's field equations are 4% wrong in the field of the Sun is enough by itself to solve the Saturn anomaly. The accepted value for the precession of Saturn is .1836 arcsec/cy.10 If we multiply that by .04, we obtain .007. That is nearly in the middle of the range calculated by Pitjeva, as you see. I solved the problem before I even knew of it.
For more confirmation of my 4% correction to GR, we may look at The 1983 experiment of Bonse and Wroblewski,11 in which they used neutron interferometry and oscillation to nearly cancel interfering beams. They found that gravitational effects were equivalent to acceleration effects in such a measurement, to within 4%. This 4% error has never been explained until now, but it is clear at a glance that my math aboves solves it. Bonse and Wroblewski used the current GR equations to calculate the equivalence of acceleration and gravity, and those equations were simply wrong by 4%.
1Which LeVerrier called Vulcan.
2Visible light confirmation, which should be relatively easy to obtain given modern instruments, has still (mysteriously) not been made available. It is claimed that radio telescopes confirmed in the 70’s, but this data is also open to interpretation.
3"After that therefore because of that", or "near that therefore because of that."
4You can either accept this as a mathematical trick, akin to Minkowski’s tricks, or you can accept it as physically real. In the context of this solution of Mercury’s perihelion, it doesn’t really matter. As a final theory of gravity, it matters a lot, but the full argument regarding that is beyond the scope of this paper.
5Einstein’s field equations use both perihelion and mean distances, since precession applies to perihelion but the entire orbit must be analyzed over a full year. That is why his number just about splits the difference of my two numbers.
6GR gives the number 3.8 arcsec/century, we are told, and observation gives about 5, but I don’t lend much credence to those numbers, for what are now obvious reasons. They are both too small to be confirmed by a theory that is so mathematically compromised.
7http://arxiv.org/abs/0811.0756
8http://www.syrexe.com/physics/2008/968393.html
9http://arxiv.org/abs/0907.4514
10http://farside.ph.utexas.edu/teaching/336k/lectures/node128.html
11Phys. Rev. Lett. 51, 1401–1404 (1983) or http://books.google.com/books?id=1yxdFAJNO9YC&pg=PA106&lpg=PA106&dq
=Greenberger+and+Overhauser+1980&source=bl&ots=oRSw3HBlQ3&sig=q4suf81OK5XpoTxmoWusSZGGODA&hl=en&sa=
X&ei=z7oXT9GEOIHUiALOvPGqCA&ved=0CDsQ6AEwAw#v=onepage&q=Greenberger and Overhauser 1980&f=false