go to homepage

A Final Simplification
of the Problem
of Special Relativity

by Miles Mathis


Part One
The Current Derivation

In other papers I have extensively critiqued the mathematical proofs of Special Relativity by Einstein, Lorentz and Minkowski. In this paper I will present the shortest, most concise explanation of the problem and its solution.
        Only one illustration is necessary, and I will again use the illustration of the spaceship flying by an earthbound observer—the one that I borrowed from a textbook and modified for use in my longer paper.



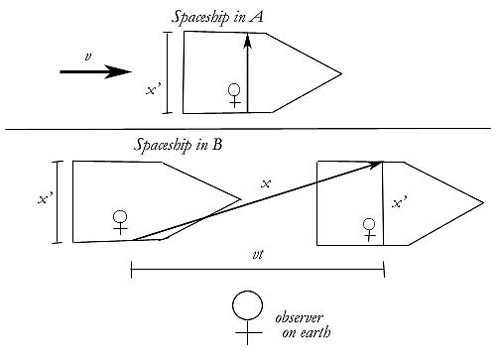
In this illustration a man walks from the near end of the spaceship to the far end. In the coordinate system of the spaceship he has walked directly away from the observer on earth, in a straight line. This straight line is x'. But from the point of view of the observer in the second coordinate system he has walked in a slant, x. This slant and the first straight line are two sides of a triangle. The third side is the distance the spaceship went from the beginning of the walk to the end. This distance may be represented by vt.
        Given x' and v, we seek x.

In order to solve, we must assume several other things. These are the first assumptions of Einstein and Lorentz and Minkowski:
x = ct
x' = ct'
        These equations are supposed to describe the behavior of light in the two coordinate systems. The only other assumption you need to solve is that we have created a right triangle here, allowing us to us the Pythagorean theorem

x = √x'² +(vt)²]

c = √x'² + v ² t² ]/t

c² = (x'² + v² t² )/t²

c² = x'²/t² + v²

c² - v² = x'²/t² = x'² c² /x²

(c² - v² )/c² = x'²/x²

x/x' = γ = 1/√(1 – v² /c² )

And there you have it, γ, gamma, the famous transformation term. It is also the transform for the t variable. Equally simple math gives us

c² = x'²/t ² + v²

c² = c² t'²/t² + v²

t/t' = 1/√(1 – v² /c² )

That is all there is to Special Relativity. This series of equations is equivalent to the math and assumptions of Michelson, Lorentz, Einstein, Minkowski, and everyone else in the 20th century. This simple algebra underlies the tensor calculus and has never been corrected to this day. Every explanation of Special Relativity you will find, no matter how complex, can be boiled down to this.

Part Two
The Critique

Unfortunately it is wrong in several places. The first place that it is wrong is in the light equations: x = ct and x' = ct' cannot both be true, because together they imply that x and t change in direct proportion, where in fact they change in inverse proportion. Einstein even admits this. In the book Relativity, he says (Ch.XII, p. 37) "As judged from K, the clock is moving with the velocity v; as judged from this reference body, the time which elapses between two strokes of the clock is not one second but [γ] seconds, i.e. a somewhat larger time. As a consequence, the clock goes more slowly than when at rest."
        Time dilation and length contraction are now cliches. Everybody knows that time slows down and lengths get shorter. But time slowing down is a lengthening of time. When time slows down the period increases, so that the length of time between two ticks is longer. This sets up an inverse relation between x and t, and makes one of the two light equations false. It turns out that the false one is the first one, x = ct. This is simply because the x in this equation is not a length measured in its own coordinate system. x is the way a length in another coordinate system looks to an observer. x is defined as the way x' looks to the observer. Therefore x = ct is not a parallel construction to x' = ct'. The two equations are not analogous. In fact, if we are given that x' = ct' (and we must be, that is one of the postulates) then x = ct'²/t. This assures that xt = x't'. Using the current equations, xx'= tt', which cannot be.
        The second mistake is in assigning the variable v in the term vt. What velocity is this? You will say it is the velocity of the spaceship, in this example. But is it the velocity measured by the spaceship or by the observer? The two will measure different velocities, but we are not told which it is. The variable is undefined. Likewise the t variable in vt. Because v and t are unprimed we assume they are measured by the observer, but if the observer already has a velocity in hand, why do we need a velocity transform later on? The velocity transform of Special Relativity claims to transform a v' into a v. But if we already have a v then what do we seek? You will say that v is the velocity of the spaceship and that the velocity transform allows us to calculate the velocity of the man walking. But shouldn't the spaceship require transforms too, not just the man? The spaceship is moving, therefore it is not in our coordinate system, therefore by the laws of Special Relativity it must require transforms. But Special Relativity never supplies these transforms.
        And this takes us to the third mistake. Gamma and the velocity transform are both generated from a conceptualization that yields two degrees of Relativity. You can see that the spaceship should require a transform itself. Then the man inside the spaceship should require a second one. The spaceship moves relative to the observer; the man moves relative to the spaceship. Relativity provides the two-degree transform but ignores the one-degree transform. In addition, Special Relativity provides the wrong transform for two degrees, as I have shown. Its math fails because its postulate equations are incorrect, its variables are undefined, and it has only two coordinate systems when it needs three.
        The final mistake is giving the spaceship in the drawing a trajectory at right angles to the observer on earth. If you will notice, the man cannot be made to walk directly away from the observer, even in his own field. His orientation relative to the observer on earth changes as time passes, so that the line x is not an accurate representation of his movement relative to the earth. The trajectory of the man would actually describe a curve in this problem. The line of equal distance from a point is a circle; therefore to remain at a constant distance from the observer on earth, the spaceship would have to orbit the observer, not go in a straight line tangent to his line of sight. This skews the whole problem. The right triangle does not have an angle of 90 degrees, for one thing, so that the Pythagorean theorem may not be used in the way it has. Furthermore, correct math will show that a spaceship passing on a tangent like this will require a variable transformation equation, one that changes every moment depending on its angle to the line of sight of the observer. A man moving on the spaceship will require even more complex transforms. The simple constant transforms of Special Relativity can only apply to movement directly away from an observer, and even there they require the corrections below.

Part Three
The Correction

It turns out that the time as measured by an observer of a moving body is simply the time of the moving body plus the time it takes for light to go from the moving body to the observing body.
t = t' + t_c
t_c = x'/c
        x' is used in this equation, because although it would seem to be only a measurement of distance by the moving body, it happens to be equivalent to the measurement of the background by the observer. In this way it becomes the background of all three: the moving body, the light, and the observer. This is the secret information that has always existed behind the problem, although it has never come to light until now. You will say that the measurement of the background by the observer is x, but that analysis is another that has been historically incorrect. In the transformation equations of Special Relativity, x stands for—and always has stood for—the way that the observer measures the moving body. It does not stand for the way the observer measures its own lengths and distances. x is the distance that the observer calculates the body to have gone, using its data. This is not the same conceptually as a length or distance within the system of the observer.
        The fact is that in SR, x' must be one of the givens of the thought problem. Einstein gives it to us by giving us v, although this has never before been clear. But if you give someone a velocity, you have given them some x over some t. This is conceptually the x that Einstein has given us: x' (although he never puts it in those terms). Of course, x' is also the variable used for length within the system of the body. This is also one of the givens or postulates of the problem, and therefore does not need to be proved.
        x' = distance in moving body's system, when measured by the moving body = distance in observer's system when observer is measuring itself.
        x = distance in moving body's system when it is measured by the observer. This is the body as seen by the observer.
x' thus belongs to what I call a local system. Even relativists believe in the local system. It is not a return to Galileo. Feynman, for instance, calls it the proper system.* In the local system, magnitudes are always measured from a negligible distance, so that the speed of light does not enter the equation or the measurement. In addition, light always travels in the local system. This is simply because every observer observes light in his own system. It is impossible to see light in another system. Our data arrives on electromagnetic waves, which waves must be in our system when we receive them, by a tautology. We measure everything relative to our own background, and we are stopped relative to that background. That is what makes it our background, of course. A background that is moving is a contradiction. Therefore, since light travels c relative to any unmoving background, light travels c in every local system. This means, of course, that there is a universal local system, defined by the speed of light. This universal local system, which is simply the equivalent of the classical universal system of Galileo and Newton, pertains whenever we are making measurements in our own system, by a method that does not require a transform. If you are measuring your own velocity relative to a given background, for instance, you are in the universal system. Only when you are measuring the velocity of a distant object are you no longer in the universal system. In this case you require a transform. The transform may be derived like this:

t = t' + (x'/c)

xt = x't'

v = x'/t = x/t'

x' = v't' = vt

t = t' + (v't'/c)

= t'[1 + (v'/c)]

t = t'/[1 – (v/c)]

v = x'/[t'(1 + v'/c)]

v =v'/[1 + (v'/c)] = cv'/(c + v')

v' = v/[1 - (v/c)] = cv/(c – v)

x = x' [1 – (v/c)]

x' = x[1 + (v' /c)]

The common term (which I have dubbed alpha) in all these transforms is
α = alpha = 1/[1 - (v/c)] = 1 + (v'/c)
t = αt'
x' = αx
v' = αv

Alpha has long been used in optics to transform frequency from one system to another. Feynman uses the equation in his Lectures on Gravitiation in a proof of gamma.
f' = f[1 + (v'/c)]
That is, he uses the correct term to prove the incorrect term. No one before me has seen that the accepted transform for frequency must be equivalent to the transformation term for one-degree Special Relativity.

Part Four
An Approaching Body &
a Trajectory at an Angle

All these transforms apply only when the moving body is moving directly away from the observer. You can see that the observer measures the period of the clock of the moving body to be greater than the period measured by the body itself: t > t'. [These time variables stand for periods, not instants, as even Einstein admitted (see The Meaning of Relativity, chapter 2, eq. 22a)]. In other words, there has been a redshift. If the clocks are thought of as waves—and clocks certainly may be called waves—then the period of the clock has been stretched by its movement away from the observer. It has been redshifted.
        Extending this reasoning, a clock approaching an observer must be blueshifted.
If t_d = period of departing object
and t_a = period of approaching blinker
t_d = 1/t_a
t = t' - x'/c
v = x'/t
v = x'/(t' - x'/c) = v'/(1 - v'/c)
v' = v/(1 + v/c)
        In this way we see that a body approaching an observer will be time-contracted rather than time dilated. In other words, the observer will measure a smaller time than the body will measure for itself: t' > t. He will also measure a larger x:  x > x'. This contradicts the current interpretation of SR.
        For simple experimental proof of this assertion, consider binary pulsars. Pulsars are clocks in the sky, which clocks create arriving waves of data here on earth. When the pulsar is moving toward us in its orbit, its period increases. The data is blue-shifted. This directly contradicts the standard interpretation of SR, which says that all relative motion causes time dilation. Time dilation is a larger period, but the motion of the binary pulsar creates a smaller period, which is time contraction. There is no way for the standard model to answer this, since if they answer that time dilation is a smaller period, then you point to the same pulsar moving away in its orbit. We have two opposite shifts here, no matter how you define them. You can't logically define both of two oppositie shifts as redshifts.

In addition, bodies moving at an angle to an observer will require complex transforms—ones that do not match either of the simple ones we have found. Trajectory must always be considered in SR. Trajectories at an angle will yield variable transforms, since the time and distance differences are not constant. These variable transforms will be dependent upon the speed, angle, and trajectory (approaching or receding) of the moving body.

Part Five
The Second-Degree Transform

To find second-degree transforms, like Einstein's velocity transform, we must expand our problem to three coordinate systems and five sets of variables:
A = man's system
B = train's system
C = system of the embankment and observer

We need five velocity variables to solve:
1) The man's velocity relative to the train, measured by the man, v'''.
2) The man's velocity as seen from the train, v''.
3) The train's velocity relative to the embankment, measured by the train, v''''.
4) The train's velocity as seen from the embankment, v'.
5) Only then can you ask about the man's velocity as seen from the embankment, v.

Let v of A rel B (man to train) = v"
let v of B rel C (train to embankment) = v'
what is v of A rel C (man to embankment)? = v
Given v' and v'', seek v.
v''' = the velocity of A measured by A.
      = v''/[1 - (v''/c)]
And we can calculate the velocity of B measured by B in the same way.
v'''' = B measured by B,
      = v'/[1 - (v'/c)]
The velocity of A relative to C, if ABC is a straight line, would be
v = v'''' + v'''
      1 + [(v'''' + v''')/c]
    = [v'//1 - (v'/c)] + [v''//1 - (v''/c)]
      1 + {[v'//1 - (v'/c)] + [v''//1 - (v''/c)]}/c
v = v' + v" - (2v'v"/c)
      1 - (v'v"/c²)

Equally simple math (not shown) allows us to find a two-degree time transform, one that is not gamma:
t/t'' =     c² - v''v'        =        1 - v''v'/c²
              (c - v'')(c - v')              (1 - v''/c)(1 - v'/c)

These transforms apply only to objects moving away from an observer in a straight line. Remember that we are dealing with observation by the use of light rays. In the observation of A from C, the light rays will travel directly from A to C. They will not necessarily pass through B. B has its own light rays from A that it is dealing with. But we should only be concerned with the light rays coming to us. That is, visual observations are made directly, and indirect evidence is dangerous in relativity. We must deal only with our own light rays, the ones entering directly into our eyes. The relativity equations apply only to these rays.
        This is not so clear when you are dealing with relative velocities all in the same line. In this case, the light rays do pass through B. But this will not always be the case, obviously. In second-degree transforms, the trajectories of both objects must be taken into account.

*He says (Feyman Lectures on Gravitation, p.94), "How much is the time difference at various points in space? To calculate it we compare the time rates with an absolute time separation, defined in terms of the proper times ds."

go to homepage
go to chapter 5

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.