More Trouble with Tides, by Miles Mathis

More Trouble
with Tides

by Miles Mathis

Abstract: I will analyze Newton's Proposition LXVI from The Principia, which is the foundation of modern tidal theory. I will show that it is false. I will then show that its extension by Maclaurin is also false. I will show that current equations fail to predict the known eccentricity of the Moon, being off by a factor of ten. I will then show the simple math proving that the eccentricity of the Moon is caused by the charge field and the Solar Wind, not by gravity.

Modern tidal theory, like many other things, comes from Newton. Newton was only a beginning, and it is admitted that he made some mistakes, but all the major additions like those of Bernoulli and Laplace and Maclaurin take Newton's basic gravitational theory as given. We can see this in recent modern books like one from 2001 by David Cartwright (of Cambridge and NASA), where the exposition of “correct” tidal theory begins with Newton's Proposition 66, from The Principia. It is this proposition that I will analyze in this paper.

Basically, this proposition shows a circular orbit thrown into ellipse by a third body. Later tidal theorists (like Maclaurin) then borrowed this proposition to show that the water around the Earth could be taken as a third body, and that it would therefore be thrown into ellipse, creating the tidal bulges we have been talking about in other papers. I have already shown that this solution has been falsified by lots of conspicuous modern data (see the negative tide on the front of the Moon, below). Here I will show the solution is illogical and false, even before any data is presented. I will also show that Newton's proposition was false to begin with, destroying the edifice at the foundation.

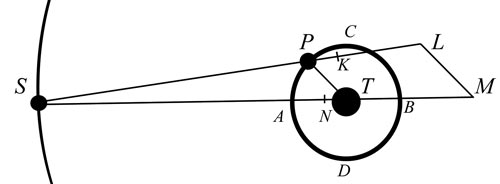
In Proposition 66, Newton gives us two smaller bodies orbiting one larger body. The larger “central” body is T, the nearer orbiter is P, and the distant orbiter is S (see illustration under title). David Cartwright and modern theorists try to get you thinking that S stands for the Sun, but if we look at Newton's initial assignments, we find that is not so. S is orbiting T, so T cannot be the Earth and S the Sun. The Sun does not orbit the Earth, and it was not thought to do so in Newton's time.

The first thing we find if we study Newton's own assignments is that he does not give us any orbital velocities for S and P. He clearly intends that his theorem will be proven for any and all velocities, so that they are not important. However, I will now show a simple falsification of his proposition, using a set of velocities for S and P. If I can show one falsification, the proposition, as stated, must be false.

Newton, in his illustration (above), draws S and P initially orbiting T in circles. His claim is that S, the outer moon, will necessarily throw P into ellipse. The case that falsifies that proposition is the case that S and P have the same time of one orbit. In other words, S is traveling much faster than P, so that the two remain in the same position relative to one another. The easiest way to see this falsification is to put P and S in the same line to start with. Nothing in Newton's set-up disallows that. Well, if that is the case, then S and P will remain in a line always, and this will only have the long term effect of increasing the radius of P's orbit. P will be thrown into a bigger circle, not an ellipse.

I will be told that Newton's math and his proposition also tell us that T will be thrown into a barycenter motion by the attractions of S and P. This must cause an ellipse. No, it causes the appearance of an ellipse only if we measure from T, and if T assumes it is static. But if we measure the orbits from S, P, or any other place in the field other than T, then P remains in a circular orbit. No ellipse is created, and Newton's proposition is false.

I will then be told that the barycenter causes an ellipse after the fact, since the barycenter creates a wobble. But the barycenter does not create a wobble relative to the two orbiters, if the two orbiters were in round orbits to start with, and if the inner orbiter is not thrown into ellipse. This is because the two orbiters, if they are stable relative to one another, only tend to pull the central body toward them. If they are stable, they pull the central body toward them an equal amount at all times, which means the central body is always the same distance away from them. So the central body can wobble without throwing the orbiters into ellipse.

This also works if S and P are not in a line. They only have to have the same orbital period. This is because P will always have the same force vector from S, and this means that the orbit will be changed the same amount all the way round. If you change a circle the same all the way around, you get a bigger circle, not an ellipse. To create an ellipse, you have to vary the change on the circle. You can do a lot of math to prove this to yourself, but it should be obvious at a glance. The only reason no one saw this with Newton is that he couches everything in stilted and convoluted language, and lots of dense geometry.

Newton's geometry fails because it contains the unstated assumption that S never moves. If S never moves, then Newton's theorem does work: P is thrown into ellipse. But Newton states that S is in orbit around T, and you cannot maintain an orbit with zero velocity. Therefore, proposition 66 is false.

We can see how confused Newton is by looking at cors. 3, 4, and 5. In these, it is clear he thinks that the ellipse is pointy in the quadratures, rather than at conjunction and opposition. In other words, he in not telling us the ellipse is pointing at S, but the reverse. In his corollaries, the bulges are not pointing at the perturber S, the bulges are to the sides. Since his main proposition is false, and his first corollaries are false, we must assume all his corollaries are false.

Newton starts corollary 5 by telling us P is closest to T at conjunction and opposition. He then switches, telling us that IF P were in ellipse to begin with (had an initial eccentricity), then “it may sometimes come to pass” that P would be farther from T at the syzygies. I take this to mean that an initial ellipse will be made more elliptical, and that the ellipse will travel.

Newton could have made it easier to understand by drawing an ellipse at some point. But instead he just draws the same circle over and over. He publishes the same stinking diagram six times in this section, and never once draws the ellipse to show us where it is.

Newton then uses the next several corollaries to push the ellipse from the quadratures to the syzygies. He creates several variations or “errors” to make the apsides travel. In the first variation (cor. 6), he lets the force from S vary. This creates a motion of the apsides forward and backward, but “more forwards than backwards.” But, again, he fails utterly to prove this “more forwards than backwards.” He says it is because KL is greater than LM (see diagram), but that is an accident of his diagram. By varying the distance of S, we can make LM equal to or greater than KL. So it is clear Newton is just pushing his numbers here. It is less clear why he is doing it. He wouldn't have needed to push his apsides to the syzygies if he had just found his ellipse pointing at S to start with, as they now do. Modern physicists no longer use this push of Newton, and it is probably because they know it is a push (supposing they can make any sense of this text at all).

But that begs this very big question: if Newton's initial proposition is false and all his corollaries are false, up to corollary 18, why have we built 300 years of tidal theory upon corollary 18? Corollary 18 is where Newton applies proposition 66 to tides. Corollary 18 is one of the shortest corollaries in this section, being less than 15 lines long, but it supports all of modern tidal theory. In it, Newton proposes that we replace the orbiter P by a fluid annulus or ring. “And the several parts of this annulus, performing their motions by the same laws as the body P, will draw nearer to the body T, and move swifter in the conjunction and opposition of themselves and the body S, than in the quadratures.”

That “swifter in conjunction” means that once again Newton has his ellipse pointing the wrong way. The apsides are in the quadratures, which is opposite the modern drawings. More than that, in this corollary 18, Newton never stabilizes his apsides in the syzygies. Yes, he proposes that the apsides move, but they do not move to the syzygies and stop there, as modern theory would have it. No, “the axis will oscillate each revolution.”

Terrible problems there, but we aren't finished. The tides cannot “perform their motions by the same laws as the body P,” because the body P is an orbiter and the tides are not. Apsides are qualities of an orbit, and the tide cannot be assigned apsides. The reason for that is the particles in Newton's fluid ring “move swifter in conjunction;” but the tide cannot move swifter in conjunction. The tide need have no orbital motion, at conjunction or anywhere else, since motion at conjunction is defined as tangential motion uncaused by the field, and the tidal motion, whatever it is, in not motion of that sort.

To say it another way: in earlier parts of The Principia, Newton defines orbital motion as a compound of “innate motion” and centripetal motion caused by gravity. The innate motion is tangential motion that the orbiter carried into the orbit. It is uncaused by the field. But the tides do not and cannot have this motion. Since they are not in orbit, and since they have no innate tangential motion, they cannot “perform their motions by the same laws as the body P.”

Also, if the tidal bulges were created by an ellipse in this way, then that would mean that the bulges were the apsides of the ellipse. Since the Moon travels within 30^o of the equator, the tide should travel mainly equatorially, and mainly east to west, with a maximum speed of travel between the two bulges and a minimum speed under the bulges. Is that what we find? Not even close. Even if we give the tide some time lag, it doesn't work at all like that. If it did, we would see the largest tides near the equator. In fact, we don't. The waters of the Earth aren't even trying to orbit the Earth equatorially. If anything, they are moving east to west, because they can't keep up with the rotation of the Earth. That is not an orbit, that is a resistance to an orbit, as we would expect.

Despite all that, Newton tries (cor. 19) to force a comparison to Earthly tides by proposing that his annulus of orbiting water is now matched in speed by the rotation on its axis of T. Note well that Newton simply proposes that the period of rotation of T is the same as the period of rotation of the water. T does not cause the rotation of the water, it simply spins underneath it, the two periods of rotation matching by fiat. Is that really how we think the oceans work? Are the oceans independent of the spin of the Earth, the rotation of the Earth and the rotation of the water just happening to match? We could ask the same question about my couch. Is my couch orbiting the Earth, with a tangential velocity of its own? Or is my couch moving due to direct contact with the Earth? I had always assumed that my couch was just along for the ride, but maybe Newton and modern physicists really believe it is self-propelled.

Honestly, I have to laugh sometimes. When reading Newton I have to look twice at the cover, to be sure I am not reading Swift by mistake. Passages like this one have the flavor of the Laputians' floating island, except that Swift's expositions are clearer.

By the way, Newton does get around to switching his bodies, so that by cor. 14, T and P are orbiting S. But if that is the case, we have to ask why Newton didn't just let T and P orbit S to start with. Why do all the math for one three-body problem, then switch the bodies at the last minute? It looks like a shell game to me, and we had better check his proposal. He simply states that all the math will be the same as before, but is that true? It could hardly be true, since in the first case we had two moons orbiting one body, and in the second case we have a planet and a moon circling the Sun. As just one example of how they are not equivalent, let us ask if we can propose any velocities for T and P that will keep S and P in a line. No, if we are given that P is still orbiting T, there is no velocity for T that can change the nature of that orbit relative to S. We cannot maintain constant relationships, and therefore cannot maintain circles.

Modern physicists will say, “Yes, you have shown some problems, but we don't care about that. We only care that once Newton makes the switch, defining S as the Sun, the Moon must be thrown into ellipse. If the Moon is thrown into ellipse, then the tides must be, too. You have admitted that the Moon must be thrown into ellipse, haven't you?”

Yes, I have, but the problems remain. To start with, physicists now use Newton's math in this section to show why the Moon's apsides travel. The Moon's ellipse does not always point at the Sun. It travels. If that is so, then the apsides of the tide should travel in the same way, by the same general math. Thing is, modern physicists want the apsides of the Moon to travel, since they do, but they don't want the apsides of the tide to travel, since there is no indication that they do. They always draw the tidal apsides pointing at the Moon, and they do that because if the apsides travel, there is no way to get them to meet up with the Solar bulges at the right times. Remember that the spring tide is explained as a conjunction or opposition of the Sun's and Moon's tidal apsides. But if the lunar apsides travel, they can be anywhere. A conjunction of Sun and Moon can explain spring tides only if the tidal apsides follow the position of the Moon. But neither Newton nor Maclaurin or anyone else has shown that they must. In fact, the math shows the opposite. If lunar apsides travel, then tidal apsides should, too. You cannot have it both ways.

Another problem is that by the current equations, the eccentricity of the Moon's orbit should be easy to estimate. The Sun has a force on the Moon 2.2 times that of the Earth on the Moon. At closest approach, the Sun would have an even greater relative force on the Moon. Unless the Moon moved close to the Earth at this time, it would escape. This means that by the current equations, the Moon's eccentricity would be infinity. The Moon would move in a beeline toward the Sun.

Is that what we find? Of course not. The Moon's orbit has an eccentricity of .055, but the current equations predict infinity. Off by a factor of infinity. The current math doesn't work.

I think many mainstream scientists recognize that gravity theory has many problems. But since they see no clear answers, their only hope is that string theory or brane theory may eventually come to the rescue. Until then, they are not prepared to look hard at Newton or Laplace or Einstein or any of the other big names. What we have doesn't work, but it is all we have. Therefore we must defend it, they think. Honorable, in a certain sense, but foolhardy nonetheless. If the various standard models weren't sold and defended with such certainty and gusto, more scientists would be prepared to offer corrections. As it is, only outsiders like me are “allowed” to spend any time studying alternatives. Peer pressure prevents academics from doing basic science. Only a handful of top theorists are allowed to speculate, and they have proved that they are not able to solve this one. After a century of work, they have only muddied up the water even more with all their new maths and their fancy lingo. Rather than correcting Newton or Laplace or Einstein, they have only whitewashed the old theories with ever more coats of obscuring equations. But as we have seen here, Newton was already dense and opaque enough. We did not require more density, complexity, and opacity, we required a clean-up. Now, 300 years later, we require a much larger clean-up.

Gravity by itself cannot explain tides, it cannot explain perturbations, it cannot explain resonances, and it cannot explain the size of ellipses (the actual eccentricities we see). To really begin to explain all these things, we have to have two fields, gravity and E/M. We have to have a unified field, and we have to have a unified field where E/M is large enough at the macro-level to enter the equations. In my other papers, I have begun to show how to do that.

I have shown that ellipses aren't caused by gravity at all. Ellipses are an E/M phenomenon, caused by charge field interaction. I will now show the cause of the Moon's eccentricity very quickly and directly. That number .055 is the same as 1/18, so all I have to do is show why the Sun's field is 1/18th that of the Earth. I have previously done the math showing that the Solar Wind supplies a force 2/5th that of the Moon's force on the Earth. That was my explanation of the spring and neap variations. So we just need to find the Solar Wind force as a fraction of the Earth's force on the Moon. Let's do the math in reverse, to see what number we would need to find. Obviously, we need to find that the Earth's force on the Moon is 7 times the Moon's force on the Earth. Because 2/5 x 1/7 ≈ 1/18. Fortunately, I have already shown that math elsewhere. In my long unified field theory paper, I said it this way:

So, if the Moon’s (radius x density) is 1/6 that of the Earth, then if the Moon’s number is 1, the Earth’s number is 6. And the total number for the combined field would be 7. But we want to give the entire effect to the Moon, keeping the Earth as a fixed point. So we multiply .151 x 7 to get 1.057m/s².

That is how fields work. And that is where the number 7 comes from. The Earth's charge effect on the Moon is 7 times the Moon's charge effect on the Earth. Therefore, the Solar Wind's effect on the Moon is 1/18 that of the Earth's charge effect on the Moon. And that gives us the Moon's eccentricity of .055. The Moon's ellipse is caused by charge, not by gravity. Newton's first postulate was wrong. He began by assuming that bodies influenced each other by gravity. But, in this case, they don't. Ellipses aren't caused by gravity. Neither are perturbations or axial tilts or resonances. This is not to say that I have ditched gravity. I haven't. I keep it in my unified field equations, and it is just as strong as it ever was. In fact, it is stronger, because I have shown its presence in quantum interactions, increasing its power there by a factor of 10²². But in this problem, as in all others, we have to monitor both gravity and the charge field. It turns out that ellipses are caused by the charge field.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.