return to homepage First posted October 20, 2004 Part 1
Celestial mechanics has not made much progress since Kepler and Newton. Even General Relativity only recast the old concepts in new but basically equivalent terms. Einstein did not overthrow the fundamental mathematics of gravity and orbits. The old conceptualizations and equations still stand; they are still taught in schools everywhere. General Relativity only fine tunes them, by substituting a different but basically equivalent theory (curved space for action at a distance) and a nearly equivalent mathematics (tensor calculus for calculus). Einstein never implies that Kepler and Newton's theories were wrong—they are only incomplete. Import the finite speed of light and the tensor calculus into classical theory and you have current wisdom with regard to celestial mechanics.
There are many other similar mysteries about the stability of orbits, but I think I have made my point in regard to the circular orbit. Let us now graduate from the mysteries of the circular orbit to the mysteries of the elliptical orbit. As you know, Kepler told us that all orbits are ellipses, the nearly circular orbit being only a special case. Does an elliptical orbit solve any of the problems I have outlined above? Is it easier to explain the creation of orbits and the stability of orbits? No. Kepler does not address any of the things I have mentioned above. No one addresses these problems. Neither Kepler nor Newton nor Einstein nor anyone else has tried to build a necessary connection between the tangential velocity and the centripetal acceleration, not with elliptical orbits or any other orbits. Kepler's second law states that a planet sweeps out equal areas in equal times. This is achieved by varying the orbital velocity of the planet, obviously. In this case there is no tangential velocity, as least not as there was in the circular example, since only two tangents will be perpendicular to the line from the sun (perihelion and aphelion). So it is unclear where the initial velocity of the planet, before it was captured, has gone. Is it still a constant piece of the compositional velocity, or has it been lost? How can we explain the formation of the ellipse and its stability?
As a final example of the current state of the art in celestial mechanics, let me show you a specific example from The Encyclopedia of the Solar System, a recent book [1999] published by NASA and the Jet Propulsion Lab with the cooperation of many of the top universities in the country. To tie the sun to a solar disc, we are given evidence from T Tauri stars. These stars are of roughly solar mass and they have what appear to be discs. Or, to be more precise, they have a lot dust around them. There is enough dust to obscure the stars, but it doesn’t. Why? Because it is confined to a disc and the disc isn’t in our plane of sight. So far so good. To confirm this, we look at the emission lines created by a stellar wind. We find that these emission lines are always blue-shifted. And this is where it gets silly. For the book tells us: “This observation is explained if the red-shifted lines that would be associated with gas flowing away from the observer were obscured by a circumstellar disc.” Anybody see the problem here? There are actually two problems. The first is that if the disc is not in our plane of sight, then it can’t be the cause of any obscuring of shifts, red or blue. The second problem is that the gas flowing away from the observer is on the far side of the star. If light from the star goes through it in order to make any emission lines, then the light must be going in the opposite direction of the earth. We can’t possibly see it. This whole theory is a comedy of basic logical errors.
return to updates
Celestial Mechanics
Unanswered Questions
by Miles Mathis
by Joseph Wright of Derby
apparent rari nantes in gurgite vasto
Kepler's laws still hold, Newton's laws still hold. General Relativity and contemporary celestial mechanics take them as givens, as starting points. For instance, Kepler's theory of ellipses still pertains to this day. One might say it remains the bedrock of contemporary celestial mechanics. Richard Feynman recalculated Newton's proof of the elliptical orbit using only plane geometry in his famous "lost" lecture. He had nothing to add but an updated proof. And General Relativity never questions accepted concepts like the theory of ellipses. For Einstein, the gravitational field remains a Keplerian beast, in shape and size and influence. The only difference is in calculating specific accelerations within that field.
There is one further difference of course: the genesis of that field. Kepler and Newton believed that a gravitational field was produced by a massive object, that space (if not the field) was rectilinear, and that the massive object acted directly—though in an unknown way—upon any matter within the field. Einstein changed all that, though in a less drastic way than is commonly assumed. He agreed that the field was produced by the massive object, but he theorized that the object acted on the field rather than on matter in the field. This produced a spherical field, which then acted on any matter within it. He went even further, though, for he believed that "the field" and "space" were two words for the same thing. For him they were equivalent abstractions or ideas. If the field around a massive object was curved, then space was. There was nothing left over, nothing that you could call space after you defined the field.
Notice, however, that the gravitational mechanism remains equally mysterious. Newton could not say how a massive object acted upon matter at a distance. Einstein cannot explain how a massive object curves space at a distance. There is much talk and work currently on gravitons, but none have been found. And Einstein never presented them as the mechanism for gravity anyway. He postulated that gravity waves might be produced under certain situations, and that the waves might be composed of gravitons, but he never implied that a normal gravitational field was produced by gravitons—by a transmission of influence-carrying sub-particles. For Einstein, no carrier of influence was necessary in a normal gravitational field, since matter in the field "felt no force." A particle that feels no force does not need to be acted upon by smaller influence-carrying particles. Matter in a gravitational field moves as it does because the field is curved, not because it is being influenced by sub-particles. Einstein took the electrical field as his blueprint for the new gravitational field of General Relativity, and it is equally mysterious. An electrical current is composed of moving electrons; an electrical field is not. A single electron has a charge, a charge it could hardly transmit to surrounding particles by emitting another electron. This would certainly be a reductio ad absurdum. The electrical field just is. The "field" has most often been a concept without mechanical legs—another one of those words that so successfully implies content that history has never felt the need to supply it with any. Just so the gravitational field.
Of course QED usually assumes that the E/M field is produced by the emission by all bodies of photons or neutrinos or some other force-carrying particle. The E/M field would therefore be an exclusionary field caused by bombardment. The quantum genesis of the E/M field is of course beyond the scope of this paper. But the gravitational field is not an exclusionary field—it cannot be produced by bombardment of subparticles. It therefore cannot be a strict analogy of the E/M field. It remains more mysterious than the E/M field even at the quantum level (one might say especially at the quantum level—where gravity becomes a ghost, a vanishing "force" that has no known influence).
In saying that a massive object curves space, Einstein was in many ways begging the question. He was removing the problem one more step. For Newton, the mystery was in understanding how the sun influenced the earth, for instance. For Einstein, the mystery becomes in understanding how the sun influences the space around it, which then influences the earth. It is a sort of obscurum per obscurius—explaining the obscure by use of the more obscure. We are now taught, in courses influenced by the thinking of Einstein, that the elegance of a scientific theory resides, in part, in its simplicity. Given two theories that have the same content—the same power of prediction—always choose the one that has the fewest moving parts, the fewest postulates. General Relativity fails on this basis alone; it is cut by Occam’s Razor. It not only fails to solve the problem of Kepler and Newton, it adds to it. The mystery of influence remains unsolved, and the mechanism now has two steps rather than one.
What I will show is that Kepler and Newton, although mathematically correct in most basic ways, left us with underlying theory that was incomplete. Einstein perfected the math, but left the underlying theory almost untouched. Relativity gave him the tools to fill in the conceptual holes of classical gravitational theory, but he did not use these tools to their full effect. Diverted by the tensor calculus, he lost sight of some of the simple conceptual shortcomings that his theory should, and could, have addressed. This has left us with orbital math that is a very precise heuristics. That is, it allows us to express empirical data with great accuracy. But it does not show why the empirical data is what it is. Its failures are the same failures as classical theory. [GR has some mathematical failures, too—the most important of which is the failure of gamma—but those are addressed in other papers.]
Ultimately I must take exception to Kepler's theory of ellipses. But to do this, I must go back even further. I must start with a single object orbiting a central mass, an earth orbiting a sun in a perfect circle, such as Archimedes might have understood. In this ultimately simple version of an orbit, we have only two velocities. We have a tangential velocity and a centripetal acceleration—which causes a so-called instantaneous centripetal velocity. Newton assigned the centripetal acceleration to gravity and the tangential velocity to the orbiting body itself. That is, the tangential velocity is not caused by the gravitational field. How could it be? It is perpendicular to that field, whether the field is rectilinear or curved. It is stated explicitly that the earth had this velocity before it entered the orbit. Newton calls it the body's "innate motion." A gravitational field has no braking effect; therefore, since a body retains a velocity until another force acts on it, the earth still has the velocity in orbit. Notice that if the earth had no velocity tangential to the sun's gravitational field as it was captured by that field, it would simply crash directly into the sun. So the earth must have an initial tangential velocity, and it retains this velocity after it is captured by the sun. This velocity is the velocity shown in all current and historical illustrations, one and the same.
As I said above, this analysis began with Newton when he described circular motion in Proposition I of The Principia. The orbiting body is assumed by Newton to have a velocity due to "its innate force." So this motion must be independent of the gravitational field. His assumption has never been seriously questioned.
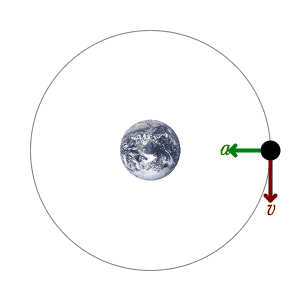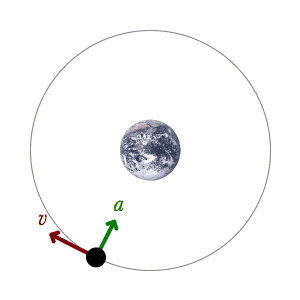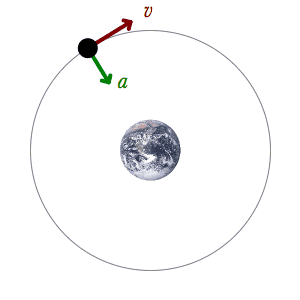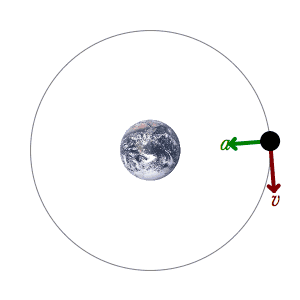
When we are shown the illustration of circular motion in our physics textbooks, we are always shown the accompanying illustration, which is that of a ball on a string. The boy whirls the ball around him, and a circular orbit is created. The force that the boy's hand must exert on the string is analogous to the gravity of the sun, we are told. The swinging action of the boy creates the tangential velocity. So in this case, the hand creates both velocities. In fact, there is a dependence between the tangential velocity and the centripetal acceleration, a dependence given mathematical form by the equation a = v2/r. But in the illustration of the orbiting earth, the sun does not swing the earth—there is no implication of that. The tangential velocity and the centripetal acceleration are completely independent. There is no string or other force that could impart tangential velocity to the earth. Assuredly, the sun is spinning, and this may create tangential perturbations in an accompanying E/M field; but there is no way, in this simplified illustration, that the sun could be the cause of the tangential velocity of the earth. And if the sun is creating tangential perturbations in the gravitational field, the theory must mechanically explain how they are produced. No theories have ever done this.
Even greater problems arise when we try to imagine how the earth was captured by the sun. How is an orbit like this created? How is any planetary orbit created? The textbooks never go there. By giving us the ball-on-a-string illustration, the book leaves the impression that the analogy is complete; that is, that the tangential velocity and the acceleration are conceptually connected in both instances. We are left with a fait accompli: since the two motions are tied to one another with the ball on a string, the two motions must be tied in the earth/sun example, and there is nothing to explain. But there is an awful lot to explain. To start with, in reality an orbit like this creates a hairline balance of two independent motions. The tangential motion and the centripetal motion must be perfectly balanced or the orbit will deteriorate immediately in one direction or another (inward or outward). Any satellite engineer knows this. There is one perfect distance that creates a stable orbit for a given velocity. Any other orbit requires the satellite to speed up or slow down—to make corrections. Obviously, the earth cannot make any corrections. It is not self-propelled. It cannot speed up or slow down. Therefore it must be taken to its optimum distance and kept there.
Now, think of the earth's orbit for a moment. Let's work backwards and see if we can imagine how the earth might get to that optimum distance, with just the optimum tangential velocity. If you reverse time, and conceptually back the earth out of orbit, you see that the only way you can do so is if you accelerate it out of there. If you keep the same velocity, it stays in orbit. If you decelerate, then it crashes into the sun. So you must accelerate the earth out of the orbit. But that means that unless the earth was ejected by the sun, it had to decelerate to reach its present position. If it is coming from outer space into the field of the sun, it must somehow decelerate in order to fall into its current position. But how can an object entering a gravitational field decelerate? It is getting closer to the sun: it should be accelerating. The only possibility appears to be a fortunate collision that accidentally throws it into the perfect spot. Even a planet ejected by the sun cannot reach any possible orbit, without a collision, since an ejected planet will not have any velocity tangential to the sun. There is no way to eject an object from the center of its future orbit with a velocity tangential to that orbit.
So, the unavoidable implication of historical theory is that all orbits must have been created by fortuitous collisions, either by planets arriving from outer space or being ejected by the sun. The problem is that planets arriving in orbits immediately after collisions are going to be damaged planets. Most likely they are going to be out of round. They are going to be missing chunks. This is a problem since imperfect planets create perturbations in orbits. Spins and wobbles are created, which cause uneven velocities and uneven forces. This should be fatal since the sort of orbit described by current theory is not correctable. There is no margin of error. Either the forces balance or they do not. If they do not, then the orbit should not be stable.
Some will interrupt here to point out that current theory provides that the earth was formed from a solar disc. It was not captured or ejected; it was simply always there, in some form. It congealed out of the nebula. But this answers nothing, for current theory fails to explain how this primordial disc of pre-planets or planetoids achieved its tangential motion in the first place (see below). Gravitational theory provides absolutely no mechanism, not even one as magical as gravity, to explain rotational motion in a gravitational field. It is the same question as to why galaxies rotate like wheels: they just do. We have a partial answer for why the stars don’t fly out into space: gravity. But we have no answer at all for why the stars move sideways to the gravitational field of the galaxy. If they weren’t captured, what set them in motion? The pat answer is “a spinning gravitational field”, but if you ask how a gravitational field imparts tangential velocity you get no answer. It is implied that the spin of the sun about its own axis somehow set the whole solar system to spinning, but this is mystical in the extreme. Almost no one thinks that the moon’s orbit is caused by the rotation of the earth about its own axis. No one thinks this because there is no mechanism to link the rotation of the earth to the orbit of the moon. There is no mechanism to link the orbit of the solar disc to the spin of the sun either, and yet it is accepted at face value.
All the other perturbations of the solar system are likewise mysterious. The planets affect eachother by applying small torques to one another, we are told. How can you postulate the applying of torques with a gravitational field—a field that is absolutely incapable of creating mechanical torques? Current celestial mechanics discovers the perturbations, gives them mathematical form, but does not explain the mechanics of the perturbations. It would be better labeled Celestial Heuristics.
According to current theory, gravity is either an attractive force or a space warp. In neither case can you mechanically explain a torque. The field is generated from its center and cannot possibly do anything but pull inward from that center. Even with a spinning gravitational field, no torque is possible. We are told that angular momentum is carried out to orbiting bodies, but how? It cannot be via the gravitational field. There is no proposed mechanism. Einstein expresses known forces with tensors, but he cannot explain the genesis of those tensors. Where do the tangential components of the tensors come from? We don’t get so much as a theory. Nothing. That is the main reason physicists have added the graviton to the fundamental field of gravity, despite the fact that Einstein assured them that objects in curved space “felt no force,” and despite the fact that they still parrot this claim—believing that GR is geometric, not force-carrying. They need the graviton to help them explain torques.
The graviton would not help them anyway. A torque could be applied by an exclusionary field—like the E/M field. But a torque could not be applied by an attractive or warping field. The graviton, if it existed, would cause attraction or the equivalent of attraction. Even if the graviton carried angular momentum, it would be a sort of negative angular momentum, like the negative force it carried that caused the body to come closer. This would put all objects in retrograde orbits, and we don’t see this. We don’t see negative torques, we see positive torques—prograde torques.
Mean motion resonances are also impossible to explain with gravitational fields, for the same reason. Gravity is a centripetal force, not a tangential force, so that resonances are beyond explanation. This also applies to tides and equatorial bulges. No one doubts they exist, but how can gravity explain them? How can curved space explain tides? Beyond curved space you are back to force at a distance—not only centripetal force but tangential force. You must have angular momentums working at a distance. How?
Another problem is that even the current model believes that some satellites, like Triton and Phoebe, are captured satellites. Captured satellites must have been captured as I stated above—by decelerating into orbit. How was this possibly achieved, given the current list of forces and causes of forces? What, exactly, caused Triton to settle into its current orbit? A balancing of instantaneous velocities cannot explain it, since even if Triton happened to intersect its future orbit at exactly the right distance and at a precise 90o angle, many other factors would also be involved. Neither Triton nor Neptune is an ideal body. They both would have had some spin. Just as an example, it is believed that all bodies apply torques to all other bodies (although it is not explained how in current theory). Therefore Neptune must have a rather complex field at all orbits, not just a simple centripetal acceleration. Scientists use this complex field to explain the motions of Neptune’s other moons. If you add this complexity to the real field of Neptune, you see that the odds of Triton arriving with all the perfect counterspeeds and countertorques, at just the right angle and distance are precisely zero. There must be some correctability to orbits not only to account for the stable orbits we see but also to account for the creation of captured orbits. The field of Neptune must have some ability to resist small deviations and to correct them. Otherwise no body could ever be captured in the first place.
It is true that the orbit of Triton is decaying, so that the orbit is not in fact completely stable. But this is not the question. No field is infinitely forgivable, but orbits show a degree of float that is not in line with current theory. There appear to be constraints on decay and escape far beyond what would be logically expected. A decaying orbit like Triton’s would be expected to fail exponentially. As Triton lost energy it would fall into a lower orbit. At this lower orbit the acceleration toward Neptune is even faster. To be in a stable orbit at a smaller radius, Triton would have needed to gain energy, or speed up. It has slowed down and gone lower, therefore we would expect a multiplied affect. Instead we see a long slow decay. Once again, empirical evidence directly contradicts the given theory of gravity and orbit.
A similar problem is caused by any three-body analysis. Insert even one moon into a planetary orbit that is the balance of a tangential velocity and an independent centripetal acceleration and you have a crash. A moon creates a perturbation that cannot correct itself. For instance, take the familiar two-body illustration and add a 3rd body. Say this 3rd body is the moon, and put the moon between the earth and the sun. We know the moon goes there occasionally because we see total eclipses. Well, the moon is going to pull the earth into a fractionally lower orbit. Physicists have never explained how this is not fatal to the orbit. They know that it is not fatal, since the earth does not crash into the sun, so they simply do the math to explain how the earth gets to the next position that it actually achieves. But to do this they must give the earth slightly eccentric little accelerations and decelerations, which they never explain. They give the earth a little tug here and there, saying that the moon corrects for itself. But this is absurd. A balancing of velocities like this cannot be self-correcting.
For instance, if you think that the moon simply pulls the earth back out of danger two weeks later when it is farthest from the sun, you are not thinking right. The moon has pulled the earth closer to the sun: in order for it to now pull it back two weeks later, it would have to be bigger. It takes a greater force to nudge a planet into a higher orbit than it does to nudge it into a lower orbit. And the same problem is going to be met when the moon is sideways to the earth. It is going to slow it down and then speed it up two weeks later. All these perturbations cannot be made to offset. No matter which direction you have the moon going (clockwise or counter) you are going to have the earth thrown into ever lower orbits for two straight weeks. The next two weeks of corrections cannot offset this. And this is not even taking into account the sun's effect on the moon's orbit, which causes further uncorrectable perturbations.
You may say that I am taking only the case where the moon is orbiting in the plane of the earth's orbit. But there is no plane of orbit that is self-correcting in this situation. I encourage you to try it.
The usual answer to this is to show a summing of potential and kinetic energies in a closed loop and prove mathematically that all energy is conserved. But this fails to address the issue. I am not complaining here about a sum or an integral. Mathematically I am pointing at differentials. If you look at individual motions in any orbit that has three or more bodies, you will find that the differentials show a variation in the tangential velocity of the orbiting body. But natural bodies like planets and stars and moons cannot vary their tangential velocites on demand of the math. As I said, they are not self-propelled. They cannot make any corrections. If the differentials are showing a variation, this variation must be explained by an external force. Gravitational theory gives us no force to explain it. Neither Newton nor Kepler nor Einstein have anything to say on the subject. It is one of the great unseen gaps in kinematics.
This is not to say that the math is incorrect. It isn't. It is simply unsupported. We have failed to build an orbit that is correctable or stable. Our engineers can build a stable orbit, our mathematicians can build a stable orbit, but our theory cannot yet do so.
This is proved once again by the large perturbation between Jupiter and Saturn, solved by Laplace. By applying a new set of differential equations to Newton's laws of motion, Laplace is said to have shown why Saturn's orbit had been increasing slightly since the time of the Chaldeans. Unfortunately, Laplace's equations hide a mechanical hole, one that cannot be filled by gravity as a pull alone. Saturn cannot go higher due to a perturbation from Jupiter, unless that perturbation is repulsive at some point in the long cycle. Laplace's equations contain that repulsion (in hiding) but cannot explain it. Newton's gravity cannot provide the mechanics for a repulsion, even one hidden cleverly in a long-term resonance.
The history of celestial mechanics is a history of mathematical analysis that is very short on theory. Every book you will find in the section on celestial mechanics at even the largest university libraries concerns creating equations to explain orbits based on observations. Three or four observations allow you to build a basic equation. Most books have differential equations on the first page, and those that don’t begin by glossing the history from Newton to Gauss—a history of mathematical analysis. Most books don’t have a single page on the theory of orbits. That is because no one has done theory since Kepler and Newton. The problems I am enumerating here are mostly not known to exist anymore, for the very reason that all study of orbits and gravity is now strictly mathematical. No one cares “why”, they only want to discuss “how”. If there are huge holes in the gravitational theories of Newton and Einstein, what does it matter? We have a heuristic theory that allows us to put our own objects into orbit, what else do we need?
As an example of this, the last two hundred years have seen work in celestial mechanics in two major areas: perturbation theory and chaos theory. Both theories are mathematical. Neither is conceptual and neither addresses any of the points I have made or will make in this paper. In fact, one might think that both perturbation analysis and chaos theory were created in order to hide the fundamental flaws of gravitational and orbital theory. Perturbation analysis hid the flaws of classical theory, and chaos theory came along later to help hide the newer flaws of GR.
Lagrange and Laplace did much work on perturbation theory, which is basically a differential or series analysis of the restricted three-body problem. Using this analysis it is found that the problem cannot be made to be completely deterministic. Poincaré showed that perturbation series are often divergent and therefore they are valid only over short time spans. Chaos theory was born out of the work of Poincaré. It investigates the causes of these divergences and indeterminacies, and their various strengths. Imprecision in some variables and operations leads to great errors and in others leads to much more limited errors.
All this is interesting, I admit. Perturbation and chaos theory is not completely without merit or use. But what has happened is that first perturbation theory and then chaos theory have engulfed and defined all serious analysis in orbital theory, so that no one even remembers what else was going on before Poincaré. Much more fundamental problems have been forgotten in order to pursue these mathematical subtleties.
Chaos math and theory closely parallels that of quantum mechanics. Both are obsessed with uncertainty. No one has yet pointed it out, but the uncertainty in both fields comes from exactly the same place. It is known that the full three-body problem becomes indeterministic when we have a four-dimensional phase space with two of the dimensions positions and two of them velocities. Sound familiar? I have shown in my paper on Special Relativity that it physically impossible to measure position and velocity at the same time, in an unknown field. Velocity requires two separate measurements: it requires a measurement of distance, then it requires a measurement of how much distance per time. These cannot be done simultaneously. This causes a HUP (Heisenberg Uncertainty Principle) even at the macrolevel, and it intersects the perturbation problem precisely here. The way that this phase space and these variables have been defined causes indeterminism. What this means is that it is the math that is causing the problems, not the physical spaces themselves.
Chaos theory sometimes recognizes this, since the fundamental definition of chaos theory is theory that explores the results of nescience in initial conditions. So it is not the variables themselves, much less the objects, that contain or are causing chaos. It is our measurement of the variables and our mathematical operations on them that are causing the chaos.
Recognition of this basic fact is not new. Mathematicians have always known that all measurements are necessarily imprecise. You cannot physically measure at a point or an instant, and this must affect all your final numbers. Furthermore, the loss of precision will depend in large part on your mathematical operations. In the simplest possible example, multiplication causes greater deviations than addition, for quite obvious reasons. Exponents cause even more problems, since they may magnify any initial imprecision. Averaging is another problem, and it happens to be the basic problem of current math. Most current math is based on series and integrals of some sort, and these integrals have a degree of imprecision even if they aren’t averaged again later.
For instance, my textbook says this, “For very long-term behavior, a fruitful approach (due to Lagrange and Laplace) involves averaging the disturbing function over the mean motions of the planets, resulting in what is known as the secular part of the disturbing function.” Well, I don’t need Poincaré to tell me that this kind of math is going to create indeterminacy. Any math that is based on calculus must be indeterminate, by current axioms, and if you add averaging to that math you have left determinacy far behind. But so what? This kind of math was not created to be determinate, it was created to be useful and “fruitful”, which it is. We must be aware of imprecision and the dangers of all our variable assignments and parameters, but we don’t have to be obsessed with them.
Chaos theory takes an interest in imprecision to places far beyond the confines of linear math. Chaos theory is often said to be deterministic, but this meaning is imprecise at best. It is deterministic only in the strict sense that it is not quantum chaos theory, for which the term indeterministic is saved. But if the HUP can be shown to apply to macro-systems, as I believe, then all chaos theory is indeterministic. This should have been seen earlier, since it is hard to imagine how a math can be non-linear and deterministic at the same time—especially when the definition of chaos depends on initial uncertainty within variables. Besides, current math theory is quite simply wrong when it claims that calculus is deterministic. [This is the other reason chaos theory is called deterministic, beyond the comparison to quantum chaos theory]. Calculus fakes a sort of determinism by assigning the derivative to a point. But as I have shown in my paper on the foundation of the calculus, this is a misassignment. There can be no change over an instant and no motion at a point.
The reason that physicists have moved to such maths may be shown by this quote from the Wikipedia article on chaos: "Everyday predictable non-chaotic deterministic systems (like good billiard tables) might seem boring because, in most cases, scientists discovered exactly how they work centuries ago, and nobody who knows how they work will ever be very surprised by them." That is to say, old physics was over and we had to find something to do. This would be a bit more convincing if there weren't so many fundamental problems still embedded in classical theory and linear maths. I myself am a new researcher in the field, but I find simple mistakes and basic holes on a daily basis—mistakes that are almost remedial and holes that almost audibly yawn. After coming face-to-face with such simple and basic errors it is very difficult to be either impressed or cowed by higher math. It is also difficult to agree with the assessment that scientists fully understand non-chaotic deterministic systems. It would be more accurate to say that scientists and mathematicians have gravitated to esoteric maths and fields in order to hide from their inability to understand simpler fields.
All this goes to say that the popular mathematics of chaos theory has obscured the fundamental problems of its field. It, along with the tensor calculus, Lagrangian and Hamiltonian math, and other higher maths, has buried much greater conceptual anomalies under a blanket of complex variables. We are taught to bow to the implications of chaos theory and to devote endless hours of modeling time to discovering which mathematical operations cause the most error. All this when we have gigantic errors staring us right in the face from direct observational data.
The errors our equations are lending us are infinitesimal compared to the errors we buy freely by failing to look closely at the world in front of us. If we want to devote time to a problem, it would be better to devote it to explaining why orbits are stable, instead of devoting it to mathematical niceties that add little to our knowledge and nothing to our concepts.
It seems to me that modern physicists hide in their math to avoid doing basic physics, a physics that is never as easy as creating models of indeterminacy in fictional fields. They prefer the chaos in their models, which is in some sense controllable and finite (if only because it can be stopped by turning off the computer) to the chaos in their basic theories, which was created by them and their precursors, and which cannot be turned off except by making better sense of it.
[Click here to read more about Laplace and the 3-body Problem.]
Let us assume that the planet can be captured at any point on the ellipse, if it arrives at that point with the proper velocity and direction. The easiest points to have it arrive, for the sake of conceptualization, is at perihelion or aphelion. So, for the sake of argument, let us say that a planet has arrived at aphelion due to some fortuitous collision. Its tangential velocity is therefore independent of the gravitational field. Meaning that the velocity is uncaused by the field, and that it is perfectly perpendicular to the field at that point. Now, if we look ahead on the ellipse, we can see that the path begins to curve toward the sun, decreasing the orbital radius. Why would it do this? We can only imagine that it must be because our planet is not moving fast enough to achieve a circular orbit. As the planet continues on, the centripetal acceleration begins to overpower the tangential velocity, and it gets closer and closer to the sun. Finally, its trajectory brings it so close to the sun that it is inside what its perfectly circular orbit might have been. This allows its tangential velocity to eventually counteract gravity, pulling it back into ever-increasing distances from the sun. So far so good. The question is, can we connect up the ellipse? Can we draw the line all the way back to aphelion? If so, then the ellipse is explained. If not, then Kepler has a problem.
To answer this, we must go back to the circular illustration. We must differentiate between the tangential velocity and the orbital velocity and it is easiest to do this in the simpler illustration. I have said the tangential velocity is equal to the initial velocity of the planet, before capture by the field. The orbital velocity is the composite of the tangential velocity and the centripetal velocity. If the earth had only a tangential velocity, its trajectory would not curve. If it had only a centripetal velocity, it would move directly into the sun. It orbits because its trajectory is a vector addition of the two. At any point on the circle, the orbital velocity is found as diagrammed below.
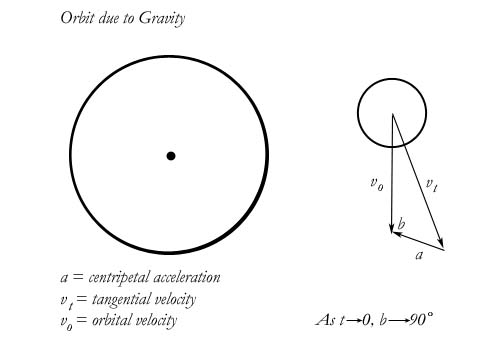
What this shows us in addition is that the earth always retains its initial tangential velocity. It still has the same perpendicular velocity it had at the point of capture. How do I know this? It is a simple deduction. There is nothing in the history of celestial mechanics that would affect this initial velocity. If it is not acted upon, it must continue, by the same rules of mechanics. Newton's First Law. And this applies to the ellipse just as it does the circle. The perpendicular component of velocity cannot be influenced by the gravitational field, therefore it must continue. Just as in the example of the ball on a string, the direction of a perpendicular velocity may be affected, but its magnitude cannot. At each point on the ellipse, the orbital velocity of the planet is the vector addition of the perpendicular velocity (which is no longer tangential) and the “instantaneous” centripetal velocity. Therefore, at perihelion, the perpendicular velocity will be equal to the initial perpendicular velocity at aphelion. The orbital velocity is much greater, but that is due only to the greater centripetal velocity. The planet is closer to the sun, therefore the centripetal component is greater.
Here is the major problem of the ellipse: Draw an ellipse with the Sun at one focus. Look at the vector additions at aphelion and perihelion, using this diagram.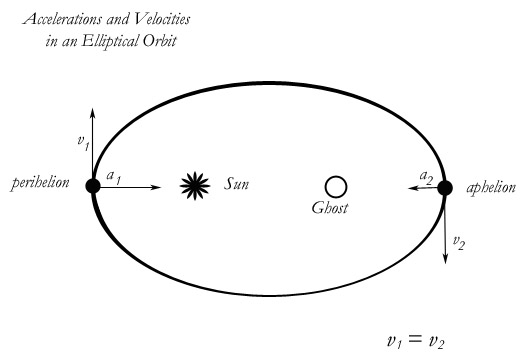
You have the same perpendicular velocities, but at perihelion the centripetal component is much larger. And yet both points exhibit the same curvature! An ellipse is symmetrical. How can this be? Celestial mechanics glosses over this problem by conflating, at various times, orbital velocity and perpendicular velocity. But they aren't the same thing.
Everyone interrupts here to scream at me that the orbiter will be going slower at aphelion. But everyone is so far missing my point completely. Yes, the orbital velocity will be slower at aphelion, but please concentrate for a moment on the curvature. If you are theoretically limited to two vectors like this, then if you slow the orbiter, you necessarily flatten out the curve. You can't draw an ellipse like this with two vectors. It's a magic trick. People have always accepted this diagram on faith, but it is a false diagram. You simply cannot draw the same amount of curvature at aphelion and perihelion and then claim that it is caused by a variable orbital velocity. An orbiter may sweep out equal areas in equal times, but not if its orbital velocity is determined by two vectors. It is a kinematic impossibility.
It is impossible since the perpendicular vector has to stay the same length all the way around. The "innate motion" of the orbiter is a constant. It cannot vary. Most of those screaming at me scream that my two velocity vectors can't be equal, since the orbital velocity varies in an ellipse. But I repeat, those two velocities are not orbital velocities. They are drawn as and labelled as perpendicular or tangential velocities. They are a component of the orbital velocity but are not equivalent to it. The orbital velocity is a vector additon of the perpendicular velocity and the centripetal acceleration. The orbital velocity varies; the perpendicular velocity cannot, sinced the perpendicular velocity expresses Newton's "innate motion". This means the only primary vector you can vary is the acceleration vector. In any gravitational field, that is the only non-compound vector that can be varying, without cheating in some way. Look closely at the diagram above. If you vary only the length of the acceleration vector, in the vector addition, then you must vary the curvature. The orbiter is going more slowly at aphelion, and this slower orbital velocity is due to the smaller acceleration vector, and only to the smaller acceleration. But if this is true, then the orbiter can't be describing the curve that is drawn by the ellipse. An orbiter with a given "innate motion" and a larger acceleration cannot possibly be describing the same curve as that same orbiter with the same innate motion and a smaller acceleration.
If we rigorously study the variable assignments of Kepler and Newton, what we find is this shape, not the ellipse: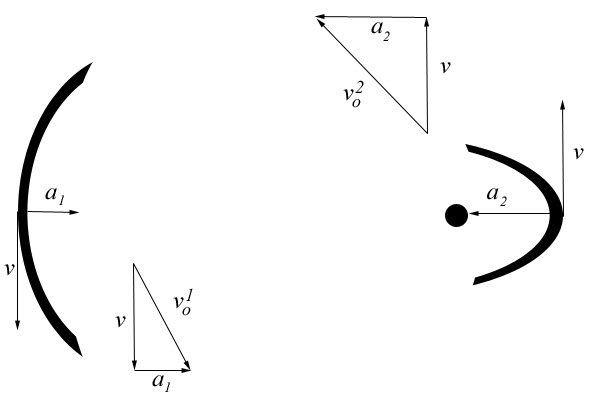
You see, the curvature cannot be the same on both sides if the innate motion or tangential velocity is a constant. This problem has been buried ever since Newton used his new calculus to find the orbital or curved velocity given the tangential velocity. In The Principia, he is given the tangential velocity or straight-line motion, and he derives the orbital or curved motion from it, using his ultimate interval (like a limit). The velocity variable in a=v2/r must then be this new orbital velocity. So the old tangential velocity is lost. It has been buried from sight ever since. But in the ellipse, or any real orbit, we must continue to monitor the old tangential velocity, since we cannot allow it to vary without giving a mechanical explanation of that variation. If we see it varying in the ellipse, as I have shown, then we must ask how a planet can vary its innate motion to suit an orbit. How can either the planet itself, or the gravitational field, cause that velocity to vary? The planet cannot, because it is not self-propelled or self-correcting. The gravitational field cannot, because the gravitational field has no mechanism to influence that vector. Even Einstein admitted that the gravitational field had no influence at the tangent. This is not to say that ellipses don't exist. We can see that they do. But they must exist with the help of some field we have not included in our equations.
Here's another problem. Say you want to recreate the ellipse with your ball and your string. You want to build a real mechanical ellipse with real forces, at a human scale. Well, you can't do it with string. But you can kind of do it with a rubber band. This will allow you to vary the centripetal force, to mimic the gravitational field of an ellipse. And yes, you can create the ellipse (sort of), and you can sweep out equal areas in equal times, and the orbital velocity is greater at perigee than at apogee. Everything looks great until you notice how your "gravitational field" is varying. The force on your rubber band is a lot greater at apogee than at perigee. What you have is a gravitational field inside out. What happened?
What happened is that Kepler's ellipse is a myth. It can't be built in the real world, by unpropelled planets in a Newtonian orbit. The reason your ball on your rubber band exhibits an ellipse is because you are able to vary its orbital velocity from the focus. You do this by varying its perpendicular velocity at perigee and apogee. Try it and see. You will find that it is easiest to give the ball a boost between perigee and apogee, since at that point a sideways nudge is felt without throwing the ellipse out of round (mostly). But a planet cannot vary its perpendicular velocity. It has its initial velocity, and that is all.
As further proof, go back to the paragraph where I am trying to build the ellipse. I start the planet at aphelion. The planet is then pulled into a tighter orbit, since its velocity is not great enough to achieve a circular orbit. I then say that the trajectory of the planet finally takes it below what its circular orbit would have been, giving it a sort of escape velocity. I imply that once it passes perihelion, its velocity allows it to begin increasing its orbital distance again. Well, this is not really true. It seems logical, and the textbooks always imply this, so it is easy to accept. But upon closer examination, it all begins to fall apart. What we imagine when we accept the ellipse as a logical-looking orbit is that it is simply a sort of squashed circular orbit. We think, well, maybe when a planet is captured, it first hits an orbital tangent at an angle, instead of at a perfect perpendicular. This throws its orbit a bit out of whack, but the orbit is somehow stable since the total area of the orbit is about the same. All very unscientific, but I would guess that many of us have assumed these things, without really questioning it very deeply. But, let's build that ellipse again, starting from aphelion. Let us draw the whole thing, just accepting that an ellipse must somehow be created, since we have evidence of them in the solar system. Finally, let us look for the "equivalent" circular orbit.
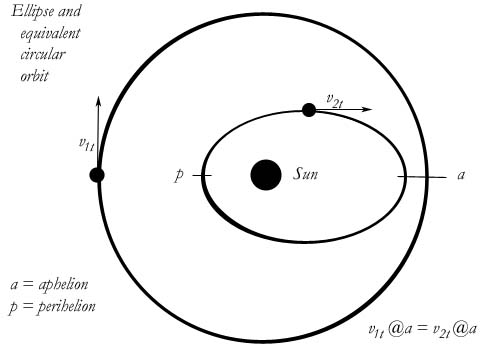
Meaning that if we have the same planet with the same initial velocity and we want to put it into a circular orbit, where do we put it? Turns out that the circle is completely outside the ellipse, and that it has a lot greater area. Remember that the only way we can explain the planet in ellipse beginning to dive toward the sun as we move it past aphelion is that its velocity is not great enough to keep it in circular orbit. Therefore, to put it into a stable circular orbit, we must move it further away from the sun at aphelion. If we do that then aphelion becomes the radius of the circle, and we have our circular orbit. As you can see from the illustration, the path of the ellipse never crosses the path of the "equivalent" circle. If that is true, then the planet in ellipse can never reach a point where its perpendicular velocity overcomes the centripetal acceleration produced by the gravitational field. It never achieves a temporary escape velocity. No, it simply spirals into the sun. Its orbital velocity increases, yes. The "orbital velocity" continues to increase until the planet burns up in the sun's corona.
As another argument, consider the standard example of the creation of an ellipse. Richard Feynman uses this example in his geometric “proof” of the elliptical orbit. Take two thumbtacks and put them some distance apart in a piece of paper. Tie one end of a piece of string to one thumbtack and the other end to the other, leaving the string with a lot of play. Now, take the point of a pencil and pull the string tight with it, making a triangle with the pencil tip and the two tacks. Pull the pencil to the left, drawing a line, at the same time keeping the string taut. Keep going as far as you can to the left and then go back as far as you can to the right. You will have half an ellipse. You can draw the other half by lifting the string over the tacks and continuing. The thumbtacks act as the two foci.
Clearly, this works because the pencil tip is feeling forces from both foci. But in a planetary orbit, the planet can feel a force only from the sun, at one focus. This is why the ellipse cannot work for such an orbit, taking the forces and velocities as they are now understood. In the thumbtack example, the pencil is feeling the same forces at both perihelions (closest to each focus). A planet would be feeling different forces at those two points.
An ellipse is simply not a potential orbit for the balancing of a tangential velocity and a single centripetal acceleration. You will say, but what about comets? We can see them. They have elliptical orbits. How do you explain that? I am not saying that elliptical orbits are impossible, I am saying that they are impossible to explain with current celestial mechanics. Elliptical orbits cannot be explained with current gravitational theory, not Kepler's, not Newton's, not Einstein's. In addition, as I have shown, stable circular orbits with moons are also impossible to explain. They should not work, since there is no reason for them to show the correctability they do show.
Here is another argument against current theory. Consider Kepler's Third Law. It states that the ratio of the squares of the periods of all potential orbits are equal to the ratio of the cubes of their average distances. This law is still accepted. Einstein accepted it. It is in all current textbooks. Furthermore, it is confirmed by the most exacting modern measurements. To within a small fraction of error, the ratio r3/t2 for the nine planets is 3.34 x 1024km3/yr2. What this means, of course, is that the orbit of the planet has nothing to do with the mass of the planet. According to Kepler's law, one must balance only the distance and the period. To see what I mean, take the Earth out to the distance of Jupiter and try to build an orbit. Could you do it? Of course. You just slow the Earth's orbital velocity down until it offsets the centripetal force from the sun. What you find is that the Earth will match the orbital velocity of Jupiter exactly. Somewhat surprising, isn't it? I assume that some readers will have thought that the Earth would be going slower, since it is smaller. It feels a smaller force from the sun, therefore it has less centripetal acceleration to offset with its velocity. But that is not how a gravitational field works. Yes, the force is different, but the acceleration is the same. F = ma. That is why all objects fall at the same rate in a vacuum, remember? Jupiter and the Earth fall toward the sun at the same rate—that is, the same acceleration—if they are at the same distance. You will say, "But the sun must pull harder on Jupiter, surely, to keep it in orbit, than on the Earth." Yes, surely. And that is my point. A gravitational field is a strange creature, and its characteristics have never been explained. They have been described, in several different ways, by Newton, Einstein, etc., but never explained. The gravitational field is not a force field, it is an acceleration field. When Newton or Einstein maps the varying numbers at varying distances in the field, he is mapping accelerations, not forces. Very mysterious, that. Notice that acceleration is a measurement of rate of change of motion. Acceleration is not directly a measurement of force. Movement, not force. That is very important.
Nor has this problem been solved by General Relativity. More money is now being spent worldwide on finding the graviton that on any other scientific project. Billions, literally. It will not be found, but a good question to ask those who seek it is this: Would the sun need to send out bigger or more powerful gravitons to Jupiter than to the Earth, if they were both at the same orbital distance? If so, how does the sun know which to send?
Perhaps we need to look for a messenger particle, one that precedes the graviton, and asks the orbiting object how much it weighs. I know that this all sounds like a joke, but the question must be addressed seriously by those who put "no action at a distance" on their t-shirts. The status quo in physics, made up of the biggest names in the field in the 20th century, still brags about this in the latest books. But their theories explain absolutely nothing.
You may be asking yourself at this point, how has all this sloppiness stayed buried for so long? Stephen Hawking told us just twelve years ago that we were a decade away from knowing everything. The end of physics. Except for chasing the graviton, no one is even working on gravity anymore. It is a problem that is considered solved. The "great minds" are busy with superstring theory, and things like that. Tying gravity to quantum mechanics. But here I am saying that no theoretical progress has been made since Newton. How can that be? One word. Obstruction.
The obstruction began with Newton himself. Newton derived Kepler's law from his own, to show that the two were consistent. He did it like this, roughly.
Given that f = ma and that F = Gm1m2/r2 (Newton's famous equations, of course)
Let f = F
Gm1m2/r2 = m1a
Then let a = v2/r
Gm1m2/r2 = m1v2/r
Next, since all the orbits of the planets are nearly circular, let the distance travelled in each orbit equal the circumference of the orbit:
v = 2πr/t
Gm1m2/r2 = m1[2πr/t] 2/r
Gm2 /r3 = 4π2/t2
t2/r3 = 4π2/Gm2
Since the right side is a constant for all planets around the sun, the left side applies to all the planets, and all possible planets.
This derivation is problematic not because we let the orbit be circular. That was only to simplify the math. The problem is in letting a = v2/r. As I showed above, this equation is applicable only when a is dependent upon v. If Newton or current textbooks want to use that equation, then they must explain how a is dependent upon v. Newton is implying that there is a necessary causal connection between the two, without providing us with a means of causation. For, I repeat, how can a gravitational field cause a velocity tangent to that field? Or, to make the analogy even tighter, how can the tangential velocity determine the field strength? That is what is happening with the ball on a string. Increased velocity causes a greater force on the string.
Kepler's Third Law tells us unequivocally that a and v are dependent, but neither Newton nor Einstein nor anyone else can say how that dependence is arrived at. Newton ties his equations to Kepler's law by a kind of cheat. He slips an equation into his derivation that contains a gigantic theoretical leap, but then does nothing to support that leap. He hoped no one would notice, and apparently no one has for about 300 years. But the fact remains that there is no theoretical justification that has ever been offered for this leap. The theory of the gravitational field, either Newton's or Einstein's, cannot support Kepler's Third Law.
People don't get famous and stay famous by putting up theories that have big obvious holes in them. So the smartest people learn to plaster up the holes and offer the theories as airtight. The very smartest people are just as good at plastering up holes, and painting over them, as they are at devising theories. Newton was one of the very smartest people. His greatest theories are full of chalk and mortar, and part of the greatness of the theories is how well the mortar has held over the centuries. But it is not just that. Subsequent scientists, unless they can devise a superior theory (which is obviously not so easy), prefer to let the mortar stand, even when it begins to show. They may even repaint over it themselves. They do this to maintain the prestige of the field. The history of physics is a history of geniuses. We all know that. And, since geniuses get paid better and make better copy, it is best to keep the field properly propped up. If Newton or Einstein is made to look foolish, we all look foolish, and our checks from the government vanish. Hobbyists stop reading about us with stars in their eyes, and Hollywood sticks to stories about old generals and ship captains and artists.
To show how contemporary physicists have painted over Newton's crumbling mortar, one need look no further than the derivation of Schwarzchild's radius and the gravity wave. Both use the same unsubstantiated assumption Newton used, namely that a = v2/r. For a famous and typical example of the derivation of the gravity wave, I refer you to Appendix V of Peter Bergmann's The Riddle of Gravitation. [Forgive me for reading these things: I know we aren't supposed to check math in appendices, but I am just strange that way.] He says that Schwarzchild's radius is R = 2GM/c2.
If a = GM/r2, and a = v2/r, then
v2/r = GM/r2
v2 = GM/r
GM = Rc2/2
rv2 = Rc2/2 or
2v2/c2 = R/r
This last equation is used to find the intensity of a gravity wave
I ~ c4R5/Gr7
The intermediate steps are not important, since they are all bombast anyway, but just note that the equation a = v2/r is still there big as an elephant and twice as invisible. It doesn't matter to anyone, even in the 20th century, that there is no reason why that acceleration should be dependent on that velocity. It was in everyone's high school textbook; why question it now.
You may answer that a = v2/r is a necessary condition of a circular orbit. It is not a matter of "dependence," as I call it. It is a mathematical necessity. Any stable orbit, whether caused by the balancing of force and velocity, as in the earth/sun example, or by a combined velocity/force, as in the ball-on-a-string example, is defined by that equation. Maybe, but that is heuristics, not theory. Using a naked equation, without any theoretical underpinning, is dangerous. The fact ends up becoming the theory, and we have forgotten that we have anything to explain. We have forgotten that the orbit of the earth is problematical, since is does not work like the ball on the string.
Another reason an equation unsupported by theory is dangerous is that it becomes dogma. It sits there, in all the same regalia as a supported equation, and we salute it in the same way throughout the centuries. It takes on the solidity of a fact, when it is not. And I am not just making airy accusations. I can show you that a = v2/r is not correct, even as it stands. It has sat on the pages of our books unquestioned since Newton. But it is false. [See my paper A Correction to a = v2/r]
Next let us look at Nebular Theory. This is the theory of how the solar system was created. Kant and Laplace were the first to propose nebular theories to explain the orbits of the planets. This was about a half century after Newton. In short, according to this theory the solar system was created by the gravitational collapse of a cloud of gases. Those who took exception to my comments about the earth being “captured” by the sun above no doubt had the nebular theory in mind, since in it no capturing of planets is necessary. The planets and the sun form at the same time. First a solar disc is created, then this disc accretes into planets over millions of years. This nebular theory is still ascendant, with a few updates that I will mention in a moment. However, I would like to point out right now that Kant is known to history mainly as a philosopher, not as a scientist or mathematician. And yet, like Kepler, his theory still stands today as the basis for all modern nebular theory. This despite all we have been told by modern scientists about philosophers being inferior creatures, ones who should not dabble in science. It is perhaps just as well for scientists like Feynman that Kant predated the chance to take their advice.
For about a hundred and fifty years the nebular theory was attacked mainly on the ground that it did not explain the lack of large angular momentum at the center of the collapse. The current solar system has larger angular momentum in the outer planets than it does at the center. That is, the sun has very little angular momentum itself. In a gravitational collapse of a nebula with some initial angular momentum, the center of the nebula would be expected to gain the most angular momentum. Many many competing theories were put forward in the 19th and early 20th centuries to explain the sun’s lack of angular momentum, but none were successful. As one recent textbook put it, they were “catastrophically” wrong. Not one was able to improve on the nebular theory. And so in recent times scientists have made their peace with the nebular theory. It has only one major flaw, whereas all the others had more than one.
Modern science has created a theory of dissipation to explain the loss of angular momentum by the sun. Several mechanisms for dissipation have been presented, although none have been very successful at explaining it. To make up for this, current theory now assumes that all the theorized mechanisms are at work, and that the actual dissipation has been achieved by their combination over long periods. What exact combination is unknown at the present time.
One of these mechanisms is the hypothesized separation of angular momentum by a two-element gas. Since nebular gases are known to be made up of hydrogen and helium (and traces of other gases), the differing forces upon these molecules during gravitational collapse is thought to have allowed angular momentum to dissipate outward. Even according to its proponents, this mechanism is not capable of explaining the actual dissipation that we see. But even more damaging to the theory is the fact that it would require that we now find a much greater concentration of hydrogen in the sun and a greater concentration of helium in the outer planets than is the case. Even if all the helium in the sun is assumed to have been created by fusion since the time of the formation of the solar system, this does not explain the ratio of hydrogen to helium in Jupiter or Saturn (the ratio is now assumed to be about that of the sun). Even if we assumed that all the helium in the pre-collapse nebula were initially positioned at the center of the cloud, and that it all was transported to the outer planets during system formation, even then that small amount of helium could not have carried all the angular momentum away from the sun.
If, on the other hand, you assume that the helium would have been transported toward the center, displacing hydrogen to the outer planets, this also fails to account for the ratio of hydrogen to helium in Jupiter and the sun. Jupiter would be expected to have almost no helium and the sun would be expected to have a lot. The sun would have the helium from transport plus the helium from fusion. But the sun and Jupiter are thought to have about equal amounts of helium.
The other mechanisms for dissipation—magnetic and non-magnetic turbulence—are equally tenuous. As is so-called long wavelength spiral structure dissipation. They all take on the form of ad hoc theories, and look very much like signs of desperation. Especially in light of my theory, which will show that dissipation is a complete myth. I will prove that the angular momentum of the sun and planets has nothing whatsoever to do with nebular collapse and that there is no nebular connection at all between the angular momentum of the sun and of Jupiter.
As a lead into this, I want to first outline some of the other flaws in nebular theory. For a proto-star or solar disc or collapsing nebula to have angular momentum after the gas begins its gravitational collapse, it must have angular momentum before this collapse. In fact, this is already assumed, since we are told that interstellar nebula do in fact have angular momenta. This has been established empirically by Doppler shift measurements on different parts of the same nebula. But nebular theory never answers the first question—that being how could a pre-collapse nebula have angular momentum? It is like saying that a gas in a jar has angular momentum. There is absolutely no known force that could cause it. A gas is either in a state where thermal forces are ascendant or where gravitational forces are ascendant. It cannot be in a state where both are primary. If thermal forces are at work, then the gas would have no center. Gravitational forces would be trumped by thermal forces, and the nebula would show no signs of gravitational symmetry—that is, movement about a center. Only if the gas were thrown out of thermal equilibrium by some temporary concentration of molecules in a central region could a gravitational collapse begin. In that case, gravitational forces would become the primary structural forces, trumping thermal forces. Therefore, nebulae which show angular momenta must already be in the first stages of collapse. And the question then becomes, how does the cloud go from being a thermal cloud with no center to being a gravitational cloud with angular momentum?
The answer is that it doesn’t. A nebula is never just a cloud of gas. A nebula requires the postulate of a center. This center is not created by the gravitational collapse, it causes the gravitational collapse. By that, I mean that the nebula does not create the sun and planets. Something must pre-exist as a center, that then creates the nebula.
It has been theorized that a shock wave from a supernova or some other outside force may start the collapse of a nebula, but it is never explained how any outside force could impart angular momentum to a nebula. The shock wave from a supernova could only impart linear momentum to all or part of the nebula, but it could not start the nebula spinning unless the nebula was already arrayed about a center.
A nebula therefore requires a seed. This argument soon becomes circular, since what I mean by seed is some massive body. But the nebular theory was proposed initially to explain the creation of massive bodies. So we require a massive body in order to create one. At first this may seem a small problem, since nebular theory explains star creation, and we need only a planet or planetoid to seed our gas cloud. But then we must explain the existence of our planetoid. Maybe it formed by simple accretion—not gravity but random collision. Accretion of what? Grain and fragments? And these grains were formed by accretion as well? If grains and planetoids formed by accretion from gas clouds, we would hardly need gravitational collapse to explain anything. But the fact is that helium and hydrogen gases do not accrete into planetoids. Gases don’t commonly just stick together for the convenience of theorists.
To sum up: the problem with nebular theory is that it 1) utterly fails to explain how a gas sets up around a center, 2) fails to explain low angular momentum at the center, as in the case of the sun.
It is not the exception, either, it is the rule. A mistake like this cannot be assigned to single person. This book was edited by a large committee of top-flight physicists. Besides, contemporary physics is riddled with basic mistakes like this, mistakes that are nothing less than shocking. I have listed many of the holes in orbital theory above, but every modern theory is full of invisible holes. My other papers might be called a compilation of these holes.
Modern physicists are trained in a topsy-turvy way. They rush through basic kinematics, vector analysis, and all fundamental conceptual physics, usually putting it behind them when they graduate high-school. They then spend their undergraduate and post-graduate years learning specialized maths. It is not that they can’t comprehend Relativity, which might be expected; it is that they can’t comprehend Newtonian mechanics or kinematics either. Most consider it beneath them. If it doesn’t involve computer modeling or advanced mathematics, they can’t be bothered to look at it. Most can’t follow a straightforward algebraic analysis with variables clearly assigned to physical objects and fields, since they are used to dealing with extremely complex and abstract variables and extremely complex mathematical manipulations. Basic physics is just not sexy anymore. And besides it doesn’t pay. You have to be a specialist. To be a specialist you have to specialize your training early, the earlier the better. Most physicists can’t afford to spend the necessary time learning basic physics, much less basic logical analysis. Anything that can’t be loaded down with variables and matrices and Fourier equations and Hamiltonians and tensors is looked upon with distrust anyway. If you speak of simple logic you are immediately dismissed as that most dangerous of all scientific demons—a philosopher.
Philosophers once policed physics in a small way, but no more. The successes of physics in the 20th century allowed it to appear to transcend any need for cooperation with “lesser” men and women. Physicists like Richard Feynman abused both the philosophy departments and the mathematics departments, and physicists cheered him. Besides, philosophy became obsolescent in the 20th century. Since Popper, no one has been capable of critiquing physics in a major way, or has even tried to. Physics, spoiled by its own notoriety, has begun to rot from within, and there is no strength in other fields to counteract this rot or resist it.
If physics is to regain any sort of health, it must begin to take mechanics and conceptual analysis seriously again. And it must regain a degree of rigor and self-criticism. Currently it is awash in a sea of self-glorification. This was evidenced most clearly by Stephen Hawking more than a decade ago, when he claimed that physics was nearly over. His popular book was a sign of the times, and a sign of things to come. Since then the science magazines have followed suit, encouraging a smug self-satisfaction while at the same time promoting increasing levels of obstruction. Lists of things that are still unknown are occasionally published, but substantive papers pointing out the very real faults of the Standard Model are dismissed without a reading and their authors are blacklisted. Besides, these lists of unsolved mysteries are always long on big theoretical problems—the sort of things that might be expected to remain even though we are brilliant masters of the universe. They are short on specific holes in existing theory. So you hear a lot about how we can’t yet explain the total amount of matter in the universe, but you hear nothing about how we can’t explain why natural orbits don’t immediately deteriorate or how we can’t explain force fields.
Science is a human activity like any other, where one would expect to find high levels of partisanship and protectionism. The history of science is a history of warfare, like history itself. But I for one think it was preferable when this warfare was in the open. In the time of Newton, for instance, scientists attacked eachother publicly and directly. This allowed a thorough airing of the differences and led to progress. We are now too interested in consensus and in creating the appearance of stability. Science has become completely politicized: we think that the daily safety of citizens depends on their believing that science has all the answers. And, I must say that this is only to be expected, since science has become the new religion. We don’t go to church to hear how all is well and “God is in his heaven.” No, we go to the web or the science magazine to hear how the demigods of physics are on the brink of explaining the genesis of all things. If we had to read an article that told us the truth—that we know next to nothing about the way things work in the universe, we would not be able to sleep at night.
The situation that science has found itself in is unscientific in itself. Science has become delusional, pathological even. It cannot look at real problems; it must invent fictional ones to divert it. It cannot study the world or even data directly; it must look through the heavy lens of a dense mathematics. Its mathematics becomes its reality. The phase field usurps the physical field, and reality evaporates. Technically, physics does not exist anymore, since the physical field has been jettisoned by QED. Only mathematics exists.
Beyond this mathematical mist in which we have lost ourselves, the other main problem is hubris. A sub-field of physics that thinks that it is perfect or near-perfect will not make any effort to improve. Until orbital physics is prepared to admit that it is mainly heuristics, it will never build beneath itself the necessary conceptual framework. The same is true of every other sub-field.
Parts I—IX of the "The Third Wave" [Book Chapters 69-78] answer many of the questions posed above. This new theory of gravity and orbits makes use of the current E/M field, Relativity, and classical equations. It is mostly a tying together of existing theory, not a GUT that jettisons the whole Standard Model or proposes mysterious new strings, branes, etherons, or supraluminal velocities. I accept c, Relativity, QED, Newton's math and most of his theory, and I give no qualities or quantities to space, including expansion. There is no force at a distance nor any attractive force (including negative charge). Specifically, the lack of angular momentum in the Sun is explained in Part IV. The explanation of the ellipse can be found in Explaining the Ellipse.
February 2010: You may now read my new paper on the Moon's orbit, which extends my comments here.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.