|
return to homepage
return
to updates
THE CORIOLIS
EFFECT
DECONSTRUCTED

by
Miles Mathis
First
posted February 14, 2011
Abstract:
I will analyze another modern theory by looking closely at a page
from Wikipedia. As I did with tides, I will go from top to
bottom, analyzing the math, the diagrams, and all the logic (or
lack of it) contained in them. I will then show that it is once
again the charge field causing the phenomena, not the Coriolis
Effect.
This
is another phenomenon that has been badly misconstrued. We are
told that bathtubs drain one way north of the equator and the
other way south, and that weather patterns spin this way, too,
whether in water or air. I will not question the data here, I
will question the explanation, which is woeful in its lack of
power and logic.
It is admitted that the Coriolis Effect
is not a real force. It is only an outcome of circular motion. A
line that looks straight from one position will look curved from
another position. Again, I am not doubting that. I accept both
the data and much of the math. However, I think it is clear that
the Coriolis Effect is only an effect of pre-Einstein relativity.
That is, it is an outcome of position and motion, not of forces
or dynamics.
Many physicists will agree with that, but I
will go further. When it is used to explain vortices on the
Earth, it is false. It cannot logically explain them. To explain
these vortices, we require the charge field.
Some will
stop me here before I get started, telling me that I don't need
to go to the trouble. We can solve this very simply without
either a longwinded mathematical analysis of the Coriolis Effect
or of the charge field. At a Penn State University website called
"Bad
Coriolis", the author, while critiquing some of the
current uses of the Coriolis motion, simplifies the argument into
this: The Earth is spinning counter-clockwise in the northern
hemisphere, and so are the hurricanes: nuff said. While I admit
that explanation is preferable to the current mainstream one in
many ways, it still begs the big question: WHY is the Earth
spinning counter-clockwise, or to the east? Why not to the west?
As it happens, the Penn State explanation is only partially
correct, and of course it doesn't even try to answer the big
question. The charge field is required to answer it because it
underlies the spin of the Earth itself, as well as the spins of
hurricanes and so on. As I will show below (and as I have already
shown in previous papers), the ambient or Solar charge field
determines all the local fields in the Solar System, and by doing
so, determines the spin direction of all the planets and moons. I
have shown how it causes tilt,
eccentricity, and
other variables,
and here you will begin to better understand how it causes spin.
If you have been following the titles of my papers this past
twelvemonth, you will have seen that the charge field causes
almost everything.
No, vortices on the Earth cannot be
caused by the Coriolis Effect alone. The easiest proof of that is
this: if the vortices were caused by the Coriolis Effect, and
switched at the equator, then there should be some point on the
equator where water drained with little or no spin. We have never
found that place, therefore the theory is falsified by data. The
theorists are required to explain the negative data, and they
cannot do it.
The simplest way to visualize the current
assignment of the Coriolis Effect to the Earth is to imagine a
merry-go-round or carousel spinning in a zero gravity field. With
no gravity, we could put polehorses both on top and below the
spinning carousel. The children could spin upside down or
rightside up. They could just crawl under the carousel and spin
on a second ride. This is the way physicists now imagine and
explain the Coriolis Effect. If the children on top see the ride
moving clockwise, the children on bottom see the ride moving
counterclockwise. Drain problem solved. The children also see
curves from center to edge reversed. Large weather curves solved.
I admit that is somewhat ingenious, which is why I
accepted it for years (without really looking closely at it). But
we encounter big problems if we let a child stand on the edge of
the carousel, right on the equator. He doesn't see any curve at
all, or at least not in the same plane as the other children. If
two children stand on the edge and throw a ball to one another,
the second child will see the ball mysteriously rise (the Eötvös
effect). The curve will be up. But the Coriolis effect proper is
gone. Do we find this in studying drains on the Earth's equator?
No. Do bathtubs drain up or fail to drain on the equator? No. Do
they drain without spin. No. Do they even drain with less spin?
No.
The Coriolis Effect also fails to explain the tight
curve of drains and cyclones and so on. The children on the
merry-go-round see curves that correspond to the curvature and
speed of the ride. They do not and could not possibly see little
vortices at spots on the ride. Nor would making the ride into a
sphere rather than a circle create these little vortices. Yes, we
find these little vortices on the Earth, but they cannot be
caused by gravity, the Coriolis effect, centrifugal forces, or
all three combined. Inertial circles, as they are called, cannot
be the outcome of inertia, or of any of these forces or
pseudoforces, as I will show below.
Another big problem
can be seen by studying the animation above. Notice the top of
the animation, which shows the effect from off the wheel, as if
we are above the pole. Well, we can go to either pole of the
Earth and look at weather from there. We can take planes and
helicopters well above the poles, or put cameras in high flying
balloons or satellites. Do they see curves in weather straighten
out? Do they see cyclones and hurricanes stop spinning? No, these
curves are real curves whose curves do not depend on your
perspective. The various vortices in weather and drains are not
caused by relativity or by position or by pseudo-forces like the
Coriolis Effect. They are caused by something else entirely.
Here's another problem. The Coriolis Effect is used to
explain the deflection of a cannonball in various thought
problems.
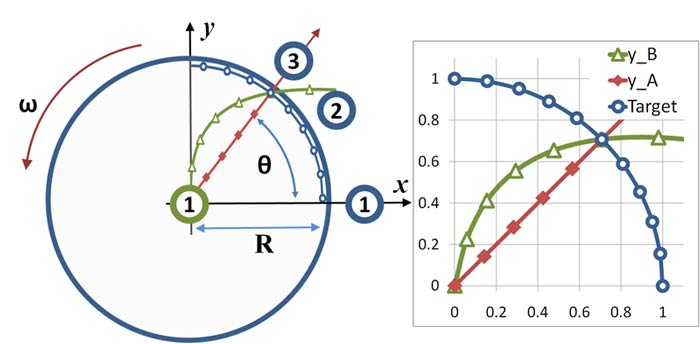
Unfortunately,
that illustration contradicts the animation below title, since we
can see there is no real deflection. In other words, it takes no
force to deflect the cannonball, since it is not really
deflected. It only appears to be deflected due to the position of
measurement. If we are looking at the cannonball from off the
turntable, we won't see the Coriolis curve; and yet in this
illustration we are off the turntable and we do see it. The
illustration is falsified. [The authors admit this, yes, but the
visuals are still confusing.] We aim ahead of the target not
because the cannonball curves, but because the target moves
toward the line. The cannonball is not accelerating, the target
is. And there is no gain in energy from the curve either, since
no force was used and no acceleration was present. Again, the
acceleration is only apparent, due to position of measurement. We
think a curve must require an acceleration, but in this case it
doesn't. The force is pseudo so the acceleration must be, too.
Well, that is a problem for hurricanes, since hurricanes don't
have pseudo-energy. They have a real energy gain from the vortex.
That being so, the cause of the hurricane cannot be the Coriolis
Effect.
Yes, the spin of the Earth creates weather
patterns. It creates latitudinal currents which, when they meet
longitudinal currents, create curves and vortices. I am not
denying it. I am not here to analyze or critique all of
meteorology. I am only pointing out that the longitudinal
currents, when curved by Coriolis Effects alone, cannot have any
real power beyond their straight-line velocity (or their
centrifugal power). They cannot be the cause of the tight curve
even in the largest hurricane, because Coriolis curves don't
curve that much. And they cannot be the cause of the energy of
the hurricane, because Coriolis curves don't have any real
energy. The curve of the cannonball in the illustration can't
have any more energy than the straight line in the animation,
since they are the same.
We can see this again by looking
more closely at a hurricane. This "low pressure system"
is over Iceland.

Notice
that we have more than a Coriolis curve here. We have three or
four complete circles. Why does that matter? Because when the
curve is moving up from lower latitudes to higher, it is actually
moving against the spin of the Earth. To put it another way, it
is anti-centrifugal. A real Coriolis curve always moves out from
the center or the pole, since that is the “force” of the
spin. Put a marble on a record player near the center hole and
then let it go. It moves out. If you put a marble on the outer
edge, it will fall off. It will never move toward the center.
Yes, if you push it hard, it will go to the center, and will
create a Coriolis curve in reverse. But you must push it. That
push is a real force. You have to counter the centrifugal force
or motion. Some force is counteracting the centrifugal motion of
the Earth in this hurricane, and it isn't the Coriolis force. We
are told that the centrifugal force of the Earth isn't that high,
but that is false. In this case, it is very high. The Earth has a
lot of angular momentum, and to get anti-centrifugal motion on
this scale and at this speed requires real forces, not
pseudo-forces.
We see the same problem when we look at
the motion of the hurricane latitudinally, or parallel to the
equator. Neither centrifugal motion nor Coriolis motion can move
that way. Centrifugal motion is always away from the pole, and
Coriolis motion is, too. Anytime the air in the hurricane is not
moving away from the pole, we require another explanation for
both its motion and its curve. With centrifugal and Coriolis
motions, we can explain motion south (in the northern hemisphere)
and west, but we cannot explain motions north and east. Just
consult the animation under title once more. The disk is spinning
east, like the Earth, and the ball is curving west.
And
this brings us to the killer punch. Look again at our hurricane
over Iceland. Now look at the animation below title. Now look at
the last sentence of my last paragraph. Do you see a
contradiction? The hurricane is backward. The Coriolis Effect
should cause a curve east to west, as you go south. The hurricane
is spinning the other direction! This is a picture of a hurricane
that is anti-Coriolis and anti-centrifugal. The subtext says it
"spins counter-clockwise due to balance between the Coriolis
force and the pressure gradient force." False. The Coriolis
force is in the other direction, so it cannot balance any
pressure gradient like this, no matter where it is coming from.
We are told that "Low pressure systems rotate in the
opposite direction, so that the Coriolis force is directed
radially outward and nearly balances an inwardly radial pressure
gradient." Criminy, these people are shameless. They expect
you to believe that! Just look at their own diagram for this:
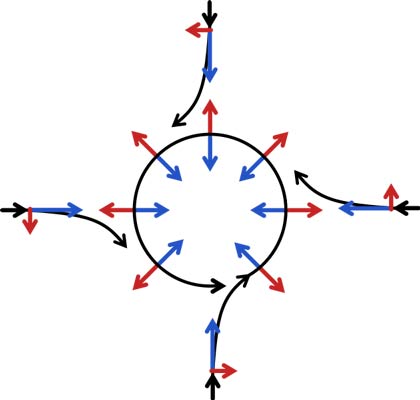
Study
the red arrows, which we are told represent the Coriolis
acceleration. Notice that we have red arrows pointing north and
east. Impossible. The Coriolis motion cannot be north or east.
Period. Ever. These diagrams are simply matched to the data, and
then the geophysicists or meteorologists just attach whatever
tags they like to the vectors, with no concern for whether they
make sense or not. They figure no one is going to study this
stuff closely, so why bother making sense.
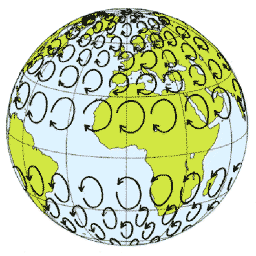
Inertial
circles also cannot be explained by the Coriolis effect, for the
same reason, and this dooms all of current meteorology. You need
inertial circles to explain low pressure circles, according to
the current math and diagrams, so if inertial circles are a
fudge, the whole thing is a fudge. In the northern hemisphere,
only the south and west motion of the circle can be attributed to
the Coriolis effect. But since there is no possible north and
east motion, we cannot complete the circle. The Coriolis effect
might be able to create half circles, but it cannot create full
circles. I draw your attention to this quote from Wiki:
An
air or water mass moving with speed v
subject only to the Coriolis force travels in a circular
trajectory called an 'inertial circle'.
Subject
only to the Coriolis force. They just
said it themselves. They are not creating these circles with any
other force or motion. Impossible. These circles are also too
small to be curves caused by the spin of the Earth. The Coriolis
motion doesn't work that way. Again, they are just matching the
diagram to data. They know that circles this size are needed to
explain the low pressure systems they see, so they create them in
the math. This is the math used:
R = v/2πf
Where
R is the radius of the circle and f
varies with latitude. Unfortunately, that math is pushed as well,
since on a spinning planet where gravity was the only other
force, you couldn't get f
to give you these small circles. This is because gravity doesn't
vary over the surface, so it can't give you a variation with
latitude. And the Coriolis effect can't either. The Coriolis
motion can only give you a greater curve as you get closer to the
equator, but it can't give you multiple curves. The fact that the
Earth is a sphere rather than a circle isn't enough to create
these breaks at latitude, where the Coriolis motion becomes flat
and then begins curving back up. For instance, what causes the
break at the two tropic lines? Why circles below, then a line,
then smaller circles above? The math is pushed to match weather
data, as I said, but it doesn't match pure physics.
You
will say, "You have admitted that the Coriolis motion
creates a curve. Does the 'force' really have to apply all the
way round the circle? Can't it just push for part of the circle?
If you push someone on a circular swing, you don't have to push
all the way round. You just push once for each rotation, right?"
Yes, but that example is not analogous to this problem, since in
a circular swing the swing is tied to the center. We don't have
any such constraint here. If the rotation were already defined,
then one push could keep it going, but physicists are using the
Coriolis force to define the circle itself. That can't work with
one push, or even a push during half the circle.
The
biggest problem is the small size of the inertial circles they
are trying to create. You see, the curvature of those circles is
much greater than the curvature of the Coriolis curve at that
latitude. The Coriolis curve is really just one big curve running
from pole to equator (center to edge, same thing), as in the
first animation under title. The curvature at a given latitude is
defined by that one curve, and it can't be any other curve. Nor
does it matter where you start. If you start at 60 degrees north,
for instance, and let the Earth spin 10 degrees east, the
Coriolis curve will move an object 10 degrees west and some
smaller amount south. So what it really creates for an observer
on the Earth is a spiral. But the observer can't even observe the
spiral, since the sphere will be blocking his view most of the
time. The observer won't see inertial circles, he will see the
object in Coriolis motion move pretty much directly away from him
to the west and then disappear over the horizon. About 23 hours
later or so the observer will see the object come over the
eastern horizon, fractionally further south than it was before.
So the only circles the object is creating are latitudinal
circles, and that only because the Earth is creating them.
Neither the Coriolis motion nor the centrifugal motion is really
creating the circles. The centrifugal motion is due south, with a
curvature that matches the curvature of the Earth; the curve of
the Coriolis motion is measured in how much the spiral increases
each day. So the only circle is the circle that motion makes
around the Earth each day. The observer could not possibly see
that circle as an inertial circle, since nothing he sees ever
goes north or east. In fact, he couldn't see it as a circle at
all, since he only sees the object when it is passing him by in a
nearly straight line. I hope you can see that no hurricane could
ever hope to be created that way.
What no one seems to
understand on these pages is that the Coriolis force is
mechanically linked to the centrifugal force. You can't have a
Coriolis force without a centrifugal force, and they are tied to
eachother at all times. This is because they are both outcomes of
spin. Therefore, the Coriolis motion is always going to be to the
south in the northern hemisphere, because that is the direction
of the centrifugal force. The Coriolis motion can never have a
northern component, because if it did it would be
anti-centrifugal. If it were anti-centrifugal, it would be
anti-spin. The Coriolis motion cannot be anti-spin. That would be
like weight being anti-mass. It conflicts with the definitions of
the words. The same applies to an eastern component. There is no
possible eastern component to the Coriolis force, by definition.
This means that no observer can possibly see the Coriolis motion
make a circle, except a latitudinal circle around the Earth over
the span of 24 hours. If the Coriolis motion is never moving
north, no possible observer can see it move north. The only
observer that could see a Coriolis motion move north is an
observer moving south, without knowing it. But that is not the
case here. We do not have ignorant south-moving observers
cataloging hurricanes, with hurricanes invisible to everyone
else.
Another huge problem is encountered when we look at
friction. The Coriolis curve can only be caused when the object
making the curve has no friction. That is why "frictionless"
or very low friction turntables are used when showing the effect
at small scales. The reason we need no friction is that the curve
is caused by the difference between an observer on the turntable
moving with it (WITH friction), and an observed object moving
without friction. The difference between no friction and friction
causes the appearance of the curve. The observer spins and the
observed object does not. Therefore, if the observer defines
himself as motionless, he will see the object appear to curve.
That is what the Coriolis motion is. But this means that whatever
is claimed to be in Coriolis motion on the Earth should be
frictionless or of very low friction. That isn't what we find.
Water and air have lower friction than solids, but they are far
from frictionless. We already know that both air and water are
carried along to a large degree by the spin of the Earth, for if
they weren't it would be quite obvious. The oceans would swamp
all the Eastern shores, and the atmosphere would move to the west
at a constant and high velocity. On the equator, the wind would
always be blowing 1670 km/hr, which would be pretty hard to miss.
It is true that friction isn't the only thing that prevents this,
but it doesn't matter here. What matters is that the air and
water are NOT moving like a frictionless ball moves south on a
turntable. The air and water are moving with the Earth to a large
degree, which means they are moving along with us spinning
observers, which means we observers would not be expected to see
much of a Coriolis effect. To the degree that the water and air
spin with the Earth, the Coriolis effect is nullified. If the air
is mostly moving along to the east with you, you cannot see it
move to the west, can you?
To see how confused
contemporary physics is once more, just look at the math they
have included for Coriolis effect. This is the diagram:
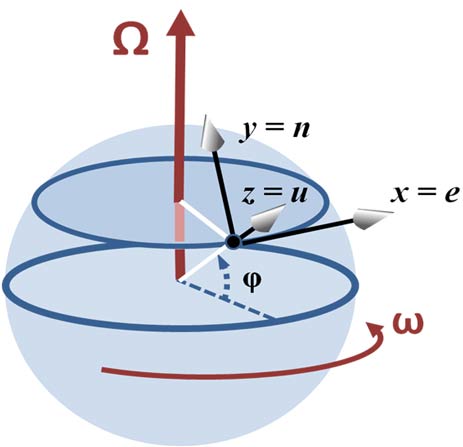
As
you see, they have their planet spinning east, and they are
diagramming a point in the northern hemisphere. But they have the
Coriolis force divided into vectors north and east! That is
upside down. The Coriolis motion in the northern hemisphere is
south and west. Actually, what they do is even nuttier than that.
These vectors they have drawn are not Coriolis motions or forces
at all, they are just samples of positive motion. They are
letting east equal +x and north equal +y. Then they find that
motion east creates an acceleration to the south and motion north
creates an acceleration east. If you aren't confused by that,
they haven't done their job, for the whole point of this math is
to make your head spin. If you are dizzy enough, you will accept
anything they say.
Ask yourself this: Why don't they just
solve for a particle placed at that point, instead of creating
these stupid initial motions? Because if they did that, you would
discover that the Coriolis acceleration on that particle was
south and west, the opposite of their drawn vectors. You would
understand what the Coriolis force really was, and then all their
other diagrams and explanations would begin to crumble in your
mind. You see, this math and diagram are misdirections. They not
only very cleverly hide from you the fact that the Coriolis
motion must be south and west, they actually fool you into
thinking it is or might be north and east. Most people won't pull
apart the math like I did, they will just look at the drawn
vectors, and they will think that the Coriolis acceleration can
be north or east. If they think that, they won't question the
other diagrams or math.
Again, consult the animation
under title. The Coriolis motion is away from the center of the
circle or away from the pole. That is the centrifugal part of the
motion. The curve is opposite the direction of motion of the
spin. So if the Earth is spinning east, the motion must be west.
The Coriolis curve must be south and west in the northern
hemisphere. It can't be anything but south and west, and it can't
create little circles to suit these people.
To counter
this, we are shown circles created on a parabolic turntable, as
if that is to the point. It isn't to the point, since the Earth
is not a parabolic turntable. But again, I don't have to do any
math, I only have to point out that the Earth cannot be analogous
to the parabolic turntable because we can now get off the Earth
quite easily. We can look at the Earth from an inertial frame of
reference just by hovering over one of the poles, and when we do
that neither the inertial circles nor the opposite spinning
weather supposedly created by them revert to straight lines. At
Wiki we get very little on the parabolic turntable, but you can
go here*
to see how it works. To the scientist watching the turntable, the
circles don't appear. You would have to go onto the turntable to
see the circles. We know they are there by using a camera above
the turntable, rotating with it at the same speed. Playing back
the film, we see the inertial circles. But two things may be said
against this, 1) I repeat that extending the poles of the Earth
creates an inertial frame relative to the Earth. If you are off
the Earth watching the Earth spin, you are like the scientist off
the turntable watching it spin. You shouldn't see the circles or
the weather they create. However, you do see the weather,
therefore the theory is false. The circles aren't created that
way. 2) Even if I can't convince you of that—because you
believe (wrongly) that Einstein proved that no frames of
reference are inertial—you should see that these inertial
circles on the parabolic turntable aren't analogous to any
possible motion on the Earth's surface, simply because they are
caused by simple harmonic motion. You see, to create the circles,
the physicists had to create harmonic motion. They needed a
closed circuit, and that is what harmonic motion is. The ball on
the parabolic turntable goes up and back, so it creates a closed
circuit, both in the inertial frame and the non-inertial frame.
But the Earth's surface isn't like that. They tell us that the
Coriolis curve is parabolic in that the curvature increases with
distance from the center or pole, but that is the curve of the
moving body, not the curve of the Earth. The curve of the Earth
is not parabolic, any more than the curve of a normal record
player is parabolic. But if they were going to turn the flat
record player into a parabola, to match it better to the math
somehow, they should have built a convex parabola, not a concave
parabola. The concave parabola, with the center lower than the
edges, creates harmonic motion and a closed circuit. But the
convex parabola can't do that, for obvious reasons. The object
accelerates to the edge and then flies off. The thing is, the
Earth is analogous to the convex parabola, not the concave
parabola. We can see that just by looking at where the greatest
velocities are. With the concave parabola, the greatest
velocities are at the center. With the convex parabola, the
greatest velocities are near the edges. The Earth is obviously a
convex parabola, in that sense, in that the greatest velocities
are near the equator. The least velocities are near the poles.
And that is true both of velocities caused by spin and velocities
due to the Coriolis motion. Therefore, the real Coriolis motion
on the Earth cannot create a closed circuit. It gains velocity as
it goes south until it reaches the equator, and then the
acceleration stops (because the curvature of the Coriolis curve
stops curving). The particle does not fly off the Earth, as it
would the convex parabola, but it stays at the equator. It does
not curve back up, because nothing is compelling it to do so. All
this is very clear I hope, so you should see that the deflection
into a concave parabola, and all the math included in that, is
just another hoax. It allows these people to create a closed
circuit where there logically cannot be one.
Wikipedia
addresses this in only one sentence:
On
a rotating planet, f
varies with latitude and the paths of particles do not form exact
circles. Since the parameter f
varies as the sine of the latitude, the radius of the
oscillations associated with a given speed are smallest at the
poles and increase toward the equator.
Funny
that these authors of a science information site have the time to
include the math for the rotating sphere, the fictitious force,
the Rossby number, the flight of the cannonball, the tossed ball,
and the bounced ball, and have time to mention the Eötvös
Effect, the parabolic turntable, ballistic missiles, and
molecular physics, but do not have time to give us more than one
sentence on this. All the other math and physics depends on this,
but this is hidden from sight! Do you not find that the least bit
strange? Well, I have shown it was not an oversight. This is all
they have to say, because this is false. "They do not form
exact circles" is hedging in the extreme, since I have shown
that they do not form circles at all. And "the radius of the
oscillations...are smallest at the poles and increase toward the
equator" is also misleading, since, although it is true, it
applies to one big curve, not a lot of isolated ones. If you do
the math on the Earth, instead of on the parabolic turntable, you
get one big Coriolis curve and no little inertial circles. That
is precisely why they divert you off into the parabolic
turntable. If the math and diagrams for the Earth showed you what
they wanted you to believe, they would have just shown you that,
right? Ask yourself why you need to be shown the parabolic
turntable, when you can just as easily be shown the Earth.
Instead, they have a section on the parabolic turntable, and no
section on how the inertial circles are created on a sphere.
It
is interesting to note that tornados are not explained by the
Coriolis force, since it seems clear that such a small tight
curve cannot be explained that way. Wikipedia says, "while
tornado-associated centrifugal forces are quite substantial,
Coriolis forces associated with tornados are for practical
purposes negligible." But this doesn't prevent even tighter
curves like drains from being explained by the Coriolis force. We
don't get a Rossby number for drains, we just get some bad and
limited experiments and the assurance that it must be the
Coriolis force once again.
And this brings us back to the
drain problem. Notice that drains in the northern hemisphere
drain counter-clockwise, like the hurricane but not like the
Coriolis motion. We should find that curious, because we now need
a lot of low pressure system, gradient force gobbledygook to
switch the direction there, too. We need a lot of very tiny
inertial circles in your bathtub, surrounding areas of low
pressure, like little gears and cogs. This would act to switch
the clockwise Coriolis motion to the counter-clockwise drain
motion.
Yes, I
have uncovered another big farce. Meteorology and geophysics
contain some good math and good models. They also contains a lot
of very bad math and very bad models, as we have seen. The
problem is that the theory under these vortex models, like the
theory of tides, conceals a big hole. In the case of large
weather patterns, we have the Coriolis Effect substituted for the
charge field. Current physics doesn't have the charge field to
work with, so it has to fill that hole somehow. In celestial
mechanics, it fills that hole with Lagrangians and other fancy
math. In these curves in wind and weather and water, it fills the
hole with the Coriolis Effect. Likewise with many smaller
effects, like the vortex of a drain. Without the charge field,
physicists can only fall back on the Coriolis Effect. But I have
shown that it doesn't work.
Notice that we would expect
the charge field to act differently north and south, since the
Earth is a sort of dipole. I
have denied that charge is dipole by the old definitions, but
I have not denied that the Earth acts as a dipole, with different
charge motions at one pole than the other. These motions are not
caused by repulsions and attractions, but they are real. In a
nutshell, the spin of the Earth causes low charge pressure at the
poles (by mechanical means only: see my other papers, most
recently the ice age paper), which causes an intake of charge
photons at the poles. But one pole intakes photons and the other
intakes anti-photons. The Earth then recycles this charge,
flinging it off most heavily at the equator (due simply to
angular momentum peaks there). Although charge is heaviest at the
equators, it is emitted everywhere. The photons and anti-photons
remain semi-sorted, however, with one being emitted more heavily
north and the other being emitted more heavily south. Again, this
sorting is done strictly mechanically, with the division being
caused by their initial velocities into the poles. They are
diverted by existing charge fields in the Earth (electric and
magnetic), but since they are coming from different directions,
they are diverted in different arcs. This is what causes the
split to remain split.
Now, the difference between
photons and anti-photons is only a difference of spin. One is
upside-down to the other. And it is this spin of the photons that
causes magnetism, as I have shown in detail elsewhere. So the
fact that you have more photons in one half and more anti-photons
in the other means that the magnetism north and south will be
reversed.
We already know that, in part. We don't know
the cause, but we know the effect. We know the magnetism is
reversed north and south, since that is what we mean by north and
south poles. If the magnetism weren't reversed, both poles would
be north, and a compass could point to either one, depending on
your latitude. But the magnetism isn't just reversed at the
poles. It is split from the equator out.
Because the
charge field is different north and south, we would expect
vortices to be different north and south. And this would apply to
vortices of every size, large and small. Since the curves are not
caused by position or by Coriolis pseudo-forces, there is no need
to explain the vortices by lots of difficult math. Magnetism is
caused by a real spin of a photon, so we can explain angular
momenta all the way down to the size of a photon. Small vortices
give us no theoretical problem. And larger vortices are just
collections of smaller ones. Because the charge field is
ubiquitous and quite strong everywhere on the Earth, every point
on the Earth will have a predisposition to vortex one way or the
other, depending on the phenomenon. But because friction and
gravity are even stronger, these predispositions show themselves
only in limited circumstances. They would be most likely to show
themselves in liquids and gasses, of course, where friction is
limited. And they would be most likely to show themselves in the
presence of ions, the heavier the better. This is why they show
themselves in weather: storms are strongly ionic. Water is also
known to be a good conductor, especially salt or mineral water,
so it is no surprise to find these vortices in water.
I
would say that the interesting experiments have not yet been done
in regards to this phenomenon. Vortex experiments should be done
at equator and pole, and compared, not only for direction but
speed. Then magnetic fields should be applied, to see how these
affect the speed at both places. Then ions should be introduced
in varying amounts, to see how this affects the speed of the
vortex. Various liquids should be introduced as media for the
vortices, using liquids of high and low conductivity. I expect
the liquids with higher conductivity would create quicker
vortices. Any or all of these experiments would immediately doom
the Coriolis explanation, since the Coriolis Effect could not
possibly be increased or decreased with ions, magnetism, or
varying amounts of conductivity.

In closing, let us look at the
actual curves. Current theory is forced to do a complete switch,
since the Coriolis force would show hurricanes spinning clockwise
and they actually spin counter-clockwise. Same with drains. This
shows that data is never a very high wall to climb, given the
right math. These mathematicians can turn night into day when
they like. But with charge, we don't need to do that. Our charge
photons are already spinning counter-clockwise in the northern
hemisphere, so we don't need to finesse pressure gradients to
explain hurricanes. Photons spin counter-clockwise, they come in
at the south pole, and they are emitted more heavily at the
equator and in the north. Since they are always present, they
predispose the entire unified field to spin with them, in the
right circumstances. In most cases, the predisposition is only
potential, but given enough ions and a lack of friction, it can
be expressed. Since the cause is the actual field particle
itself, we can explain any size vortex, even molecular or atomic
vortices. We would expect material vortices to have a lower limit
above the size of the ions present, since matter is normally
driven by ions. That is, charge is normally expressed in the
baryonic field via electricity and magnetism, which require ions.
But at smaller scales, we would expect vortices caused by the
photons directly.
I have shown that current Coriolis
theory can't explain draining at the equator, so I should have to
answer it myself. With the Coriolis explanation, there is no good
way to explain draining near the equator, which is why it is the
one question never asked or answered by the talking heads. Go ask
it to your Google search engine. I did and I got nada. With
Coriolis and Eotvos and the rest, we would expect drains to drain
poorly on the equator and to have very little or no spin either
way. That isn't what we find. How does my theory answer data? If
we have a switch from CW to CCW photons, we should still have a
line where the switch is made, right? Not really. With my theory,
we can explain local variations somewhat more easily. Like this:
Some have thought that according to my theory of recycled
charge, the equator must show more magnetism than other points on
the Earth. Their reasoning was this: if more charge is being
emitted there, and assuming no lack of ions there, we should see
stronger magnetic fields. That is a logical conclusion, but it
fails for this reason. We have more charge, yes, but we have both
photons and anti-photons. Both are being emitted, and both are
being emitted in large quantities. So unlike with Coriolis
theory, the equator is not a zero line or a minimum line, it is a
maximum line. It is the maximum for both photons and
anti-photons. Well, since spins cancel, this would mean that the
magnetism would cancel. So by this way of looking at it, we
should have more electrical effects on the equator and less
magnetism. In fact, the two mechanisms offset: high charge means
more magnetism and the high presence of both spins damps this
added magnetism back down to normal levels. So the equator is
neither much more nor less magnetic than other points on the
Earth. It has more charge, and so we would expect stronger
electrical fields, but not magnetic fields. Since it is the
magnetic fields that cause curves, we wouldn't expect drains to
act differently on the equator.
You will say, "But
if we have equal amounts of photons and anti-photons, the
magnetism should be zero, right? That is how you are explaining
the lack of magnetism of Venus, if I remember." That is
right. So we don't have equal amounts of photons and
anti-photons. The Earth is not recyling equal amounts of each.
The strong magnetic fields here tell us that we have a
predominance of one over the other, and that is because the
ambient field from the galaxy and Sun is unbalanced. As we have
seen from studying
Venus, it is the fact that she is upside down that causes the
lack of magnetism. She recycles plenty of charge, it just gets
cancelled in terms of spin when it meets the ambient charge
field.
So why is the galaxy producing more of one than
the other? Because the galaxy is spinning one way and not the
other. Why is the galaxy spinning one way and not the other?
Because that is the way it happens to be positioned relative to
other nearby galaxies. That is the way the "gears" set
up here. And, yes, it could be otherwise. Not all galaxies spin
the same way.
But back to the Earth. This must imply that
the northern hemisphere should have more charge. Do we have any
indication of that? Yes, we have many hurricanes in the North
Atlantic, and almost none in the South Atlantic. Local magnetic
fields hit a minimum in the southern hemisphere, in South Africa
and South America.** We have more storms to the north overall,
and although this used to be explained due to less detection in
the south, this is no longer true. With satellite coverage of the
entire Earth, we have found that there is indeed more "weather"
in the north. This has also been attributed to greater landmasses
in the north, but it may be that both the greater landmasses and
the greater weather is caused by the same thing: more charge.
Just as the planets inhabit the plane of greatest charge in the
Solar System, it is probable that the land inhabits the area of
greatest charge on the Earth. I will give you more reasons for
that as my papers on charge continue to unfold.
I have
said in many papers that celestial bodies emit more charge near
the equator and less near the poles. In previous papers I
provided a link from NASA of actual
footage of the spinning Sun, and it is clear from a glance
that more charge is being emitted near the Solar equator. Do we
have any similar glaring evidence on the Earth? Yes. We have
known since the 1960's that the ionosphere is considerably weaker
near the poles. As just one example, we are told in a paper† by
Grote Reber (a pioneer of radio astronomy) that
Since
these long waves must get through the ionosphere, the best
locations for observing will be where the electron density is
lowest. Examination of a vast amount of ionospheric data
disclosed that there are two bands of about 35o
latitude radius centered on north and south magnetic magnetic
poles that meet this requirement.
I
have said that charge drives ions, and here we have direct and
longstanding data that we have fewer electrons being driven near
the poles. That is direct proof that we have less charge at the
poles. The only way to deny it is to say that E/M isn't driven by
charge. That would be novel, since all of QM and QED and QCD is
based on the idea that E/M IS based on charge. I have never
disagreed with mainstream theory in this, I have simply given
charge a real presence, rather than a virtual presence. And I
have given it a real presence at both the quantum and macro
levels. We know from data of these charge holes at the poles, but
they have never been explained. I have never seen an explanation
attempted. But, as you see, it is a natural outcome of my theory
of charge recycling. We have less charge at the poles because
charge is coming in there, not being emitted there. So we
wouldn't expect ions to be driven up. They would be driven down
at the poles, if anything. And these ions moving toward the Earth
would not impede incoming cosmic radiation like ions moving up.
More evidence we have for more charge in the north is
that the Earth's magnetosphere is imbalanced to the south. The
magnetosphere is not the same size top and bottom, as it would be
with a true dipole. I have seen this attributed to the tilt of
the Earth and other factors, but obviously it can't be tilt,
since the Earth is sometimes tilted toward the Sun and sometimes
away. If the tilt were the cause, the shape of the magnetosphere
would switch every six months. Again, imbalanced charge (parity
violation of the entire field) is the most logical answer.
For
now, we will return to the spin of the Earth. I said near the top
that charge not only caused the spin of hurricanes and so on, it
also caused the spin of the Earth itself. How does it do that?
Simple mechanics, as usual. All my photons, including charge
photons, have real mass and angular momentum. Even standard-model
photons have real momentum, for if they didn't we wouldn't have a
photoelectric effect. Well, during this recycling of the charge
field, the photons have to be curved or redirected by the
interior of the Earth. I said above that this was done by fields,
but that was shorthand, of course. In my theory, fields like this
are collision fields. The entire charge field is a collision
field, when you get right down to it. Just as with Feynman's
sumovers, what you have with photons is a stupendous amount of
field collisions, and you sum them to get your overall motion.
Some photons will go right through the Earth without a collision.
Some will crash head-on into an anti-photon, losing spin and
energy and being "demagnetized". But the median or
defining photon will appear to create a nice curve, going from
south pole to just above the equator, say. The many collisions
this photon encounters will sum into this curve, and the bulk of
the photons will follow that curve, more or less. It would take a
lot of math to show that curve, and this paper is already overly
long, but I think that curve is fairly intuitive, once you
understand the mechanics. If you have a spinning Earth and
spinning photons, and a dipole configuration with opposite spins
coming in at opposite poles, you are going to get curves. I hope
you can see that without all the math.
And so, given
that, you only need to add the fact that these collisions in the
Earth's interior transfer momentum and angular momentum. When the
photons collide with matter in the Earth, that matter feels a
tiny push. If we sum all the collisions, the Earth feels a force.
It feels a force in the direction of motion of the photons, it is
that simple. We don't have to do any mathematical switcheroos.
So, due to linear momentum, charge coming in at the poles tends
to make the Earth a bit smaller, and charge going out at the
equator tends to make the Earth a bit larger. That is the answer
to that question, not the given one. The radius at the equator is
greater due to photon pressure from within. And the Earth is
flatter at the poles due to photon pressure from without. The
angular momentum of the photons is transferred to the Earth in
collision as well, causing spin.
This would create spin
even if we only had photons coming in at one pole, but photons
coming in both poles doubles the effect. Since I have shown we
have more photons than antiphotons, we must have more flattening
at one pole than the other. In fact, this is precisely what we
find. The south pole has a fraction more flattening than the
north pole, and this is the cause. The south pole is being
flattened by the same cause that obliterates the nearside crust
of the Moon: charge photon bombardment. Interestingly, I
predicted this flattening before I knew of it. I wrote it into
this paper, and only then Googled on it. Fortunately, I found
this
and much more. If you prefer the current answer to greater radius
at the equator, consult the current answer for an explanation of
more flattening at the south pole. The Earth's angular momentum
obviously can't answer that one, nor can centrifugal forces. And
gravity from the Moon can't answer it either. Charge is the
pretty obvious answer, to this as well as to many other
questions.
If you take that last link, you will find that
we also have a small bulge at the north pole. Can current theory
tell you why? No. But I saw the answer immediately. Since the
ambient or Solar field is not balanced in terms of charge (see
also my paper on parity
violations), this causes an imbalance in matter/anti-matter.
Yes, the Earth has more matter than antimatter (though it does
have antimatter). This means that anti-photons are coming in at
the north pole, there meeting a body composed of matter. This is
not disallowed, but it does create a local field response. The
incoming charge cancels the local charge, as a matter of spin,
and the flattening that would normally take place is damped down
locally. The flattening effect of the incoming particles is
lessened, since they don't have an angular component to their
momentum. This makes the local surface seem to rise relative to
the area around it.
Because we have more charge entering
the south pole, we should find that the aurora australis is more
intense than the aurora borealis. I have no data on this. We
should also find less local magnetism at the north pole than at
the south. Again, I have no data on this.
For more on
related topics, you can visit my paper on why
warm air rises. Low pressure systems are currently explained
by warm air rising, but there has never been a clear mechanical
explanation of why warm air does rise. Again, I show we need the
charge field to explain it. Other comments on weather and
meteorology may be found in my
paper on how various structures, including lightning rods,
mountains, and pyramids, focus the charge field and thereby
influence weather. My paper on atmospheric
pressure may also interest some readers, since it is there
that I do the math proving the presence of the charge field in
the atmosphere.
*http://www-paoc.mit.edu/labweb/lab5/inertial%20circles/inertial_circle.pdf
**http://en.wikipedia.org/wiki/Earth's_magnetic_field#Field_characteristics
†http://www.21stcenturysciencetech.com/Articles_2011/BigBang_Bunk.pdf
p.3
If this paper was useful to you in
any way, please consider donating a dollar (or more) to the SAVE
THE ARTISTS FOUNDATION. This will allow me to continue writing
these "unpublishable" things. Don't be confused by
paying Melisa Smith--that is just one of my many noms de
plume. If you are a Paypal user, there is no fee; so it might
be worth your while to become one. Otherwise they will rob us 33
cents for each transaction.
|