|
return to
homepage
return to updates
The
Cause of Axial Tilt
Part 1
by
Miles Mathis
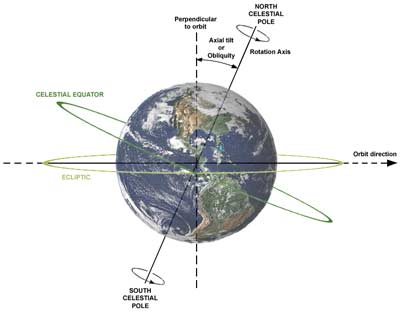
Abstract: By doing simple
calculations on Mercury, Uranus, and the Earth, I will show that
the tilts are easily calculable from perturbations, and that
these perturbations can be calculated from only three numbers:
mass, density, and distance. This will overthrow the entire
history of Celestial Mechanics.
Here we have yet another example of
extreme negligence by the mainstream. This problem, like a
thousand others, is passed over as uninteresting, while we aim
our telescopes at the edge of the universe and conjecture
extensively about the first few seconds after the Bang. It would
appear that real problems, close at hand, are too difficult, and
we must misdirect all attention into the esoteric and arcane,
billions of light years beyond our data and understanding.
If
you do a websearch on this question, as I recently did, you find
that the answer is “a collision.” Yes, it is thought
that all the planets gained their various tilts by accidental
collisions in the distant past. That answer is so gloriously lazy
and uninspired that at first I could not believe it. I thought
that perhaps I had arrived at the Flat Earth PR page, and was
reading another hedge from the hedge. But no, this is apparently
as good as we can do on this one. It is somewhat like finding a
squashed highway cone in the street and assuming it grew there
that way.
It may be that the reason mainstream physics
has never even tried to solve this one is that it doesn't have
the tools to do so. Although the problem doesn't seem that
difficult, on the face of it, it does require you to have a few
cards in your hand, a few broad ideas in your head. One of those
broad ideas is the E/M field, which the mainstream has never had
in its celestial mechanical hand. True, the mainstream knows that
the tilt is the tilt of an axis, and they know that the axis
seems to have something to do with the E/M field of the body, but
they don't know that distant bodies can effect eachother via that
same E/M field. Not so long ago, they didn't even know about
magnetospheres and plasmas. Now they will admit that the near
environs of a body can be affected by E/M fields, but they still
resist letting that field permeate the Solar System. Why? Because
if the E/M field got involved in perturbations, several major
fields of enterprise would tremble at their very cores.
Perturbation theory and chaos theory would be in danger of
ultimate extinction, and gravity theory would have to be
overhauled from the foundation. These astrophysicists would also
have to admit that Velikovsky was at least partially right, and
they would rather tear out their own eyeballs and eat them than
go there.
Well, it is all very sad, I am sure, but the
winds will blow and the grass will grow. I have shown that
Newton's and Kepler's
own equations contain the E/M field, in very simple form, and
always have. This means that the mainstream physicists can keep
their prized equations, but they will have to re-adjust their
belts in some rather conspicuous ways. The unified field they
have sought for a century was hiding in plain sight, and it will
be an eternal embarrassment to generations of ghosts to have
missed it, and to have looked for it in strings and bosons and
dark matter and so on.
[To see mainstream data in
conspicuous agreement with my analysis here, you may go to
Wikipedia and type in "Heliospheric
Current Sheet".]
This E/M field is the card I had
in my hand that allowed me to see through the tilt question
immediately. You only have to look at a few lists of numbers to
get a feel for the solution. Let us list the actual tilts of the
eight planets, then list masses relative to the Earth, then list
the relative distances between planets, with Mercury's distance
as 1.
0.01
0.05
1
2.6
0.82
0.86
23.4
1
0.71
25
0.11
1.33
3
318
9.5
26
95
11.3
97
14.5
24.9
28
17.1
28.1
The first thing we see is that we have four planets
within a few percentage points of one another. The Earth, Mars,
Saturn, and Neptune all have similar tilts. That is unlikely to
be a coincidence. If we measure those four tilts relative to the
Sun's equator, instead of relative to their individual orbits,
the numbers are even closer, being 30.55, 30.65, 31.51, and 34.4.
Another big clue is Mercury, with no tilt. And the final big clue
is Uranus, with a near 90o
degree tilt.
Let's start with Mercury. Like all other
planets, Mercury has bodies on both sides of it. On one side, we
have the Sun; on the other side, Venus. Because the Sun is so
huge, it overwhelms all other influences. So we may treat Mercury
as perturbed only by the Sun, in the first instance. Mercury
orbits very near the Sun's equator, at an inclination of only 3
degrees, 4 degrees closer than the Earth. Mercury is also
furthest from the invariable plane, and this proves again that it
is influenced more by the Sun and less by Jupiter and the other
planets, as would be expected. But it must be influenced by the
charge or E/M field, in this case. Mercury is matching its tilt
and inclination to the Sun, and in doing so it is matching itself
to the ambient E/M field, not the gravity field. The gravity
field has no mechanism for influencing Mercury's tilt or
inclination, since it is all the same to gravity whether Mercury
orbits east-west or north-south. The field equations of Kepler,
Newton, Laplace, and Einstein all fail to provide a mechanism for
tilt or inclination, which is precisely why current
astrophysicists still give tilt and inclination to accident or
collision.
In a moment I will show exactly how the charge
field (which I have shown underlies E/M) causes this phenomenon,
but for now let us just look at the effect. I propose that a body
that is perturbed by a charge field from only one direction will
have no tilt, and that a body that is perturbed equally from two
opposing directions will have a tilt of 90o.
Tilts in between are caused by uneven forces, and may be
calculated from the sizes of the forces.
Just to be
clear, I am proposing new perturbation theory. Below, I will
solve multiple-body problems by calculating real mechanical
forces upon those bodies. This will be the first serious
mechanical work done on the field since Laplace “perfected”
Newton's equations 230 years ago. Because Laplace's equations
were so successful as a heuristic model, no one has bothered to
try to prove that he was completely wrong, as a matter of
mechanics. Yes, Laplace's equations are celestial math, not
celestial mechanics. Neither Laplace, nor for that matter Newton
or Kepler, ever did any celestial mechanics. And no one has done
any since then. Conversely, my equations below will be shown to
be fully mechanical. My charge field cause forces by bombardment.
That is, particles must touch.
There are no attractions and no forces at a distance, not in the
gravity part of the unified field and not in the charge part of
the unified field. The entire unified field is mechanical, and
resolves to motion and contact. All equations are explained and
underpinned, and all the math is simple and transparent.
So,
back to Mercury. In this case, Mercury has almost no tilt because
the Sun overwhelms the field coming from the other direction. We
can even do a bit of rough math here. Mercury's tilt+inclination
relative to the Sun's equator is about 3.39o,
which is 3.76% of 90o.
The mass of the rest of the Solar System is about .134% of the
Sun's mass, and the average distance of the mass is about 23
times the distance of Mercury.
23 x .134% = 3.1%
That
is why Mercury is tilted. The Sun is 97% of the effect, so
Mercury can tilt only 3%. That is very rough math, since you have
to calculate each perturbation separately, but it gets us
started.
You will say, “Good Lord, shouldn't you
have divided by 23 rather multiplied? The planets are further
away from Mercury than the Sun. Surely the charge diminishes with
distance? In other papers, you show the charge field diminishing
by 1/R4.”
Yes, I show that when the charge field leaves a given spherical
body, it diminishes by that rate. But that is not what is
happening here. The charge field of the Solar System has to be
taken as one spherical field. Imagine that the Solar System is
one big ball. When charge is emitted out from the center of that
ball, it diminishes. When it is emitted toward the center, it
increases. The entire field is defined by the Sun, and shaped by
the Sun, so the radial lines of the main field come out from the
Sun. If that is true, then the field lines get closer together as
you get nearer the Sun. When field lines get closer together, the
field gains density. Therefore, the effects of outer planets on
inner planets are relatively greater than the effects of inner
planets on outer ones. One way to look at this is to recognize
that inner planets are emitting out into larger shells. The
surface area and volume of these shells increases with increasing
distance from the Sun, so the charge field loses density for that
reason. But in the reverse case, the charge field density must
increase, because the outer planets, when perturbing inner
planets, are emitting into a smaller orbits and smaller shells.
You will say, “But the Solar System is not
enclosed. What keeps emission from outer planets from escaping
into space?” When the emission is away from the Sun, very
little. The Sun's charge field lines can only channel it, but
they cannot keep it from traveling out into space, since that is
where it is going regardless. But when the emission is traveling
toward the Sun, the Sun's field lines channel all charge toward
the Sun. The charge field out from the Sun is constant and
relatively heavy, so it is a pre-existing stream that any new
emission must be affected by. Some emission from outer planets to
inner ones will be lost to space, but the bulk of it joins the
stream, and is channeled into ever denser fields, until it
perturbs an inner body or is recycled through the Sun's poles. To
read more on this, consult
my recent equations on the magnetosphere.
Now you
will say, “But you didn't square or quadruple your effect.
If the density increases as we go in, shouldn't it follow a
square law, at least? How can you just multiply by 23?”
Once again, you can't just follow equations, you have to follow
mechanics. Yes, the charge field will square because we are going
to smaller surface areas, but we are still in the gravity field,
too. We are in both simultaneously: the unified field. You can't
go toward or away from a gravity field, in this case. You are
either in one or you are not. Gravity is still the inverse square
(relative to the charge field), and the charge field is now
squared, since we are moving in. So the two together cancel,
giving us a field that simply increases with distance. If we
follow the charge field out from the Sun, we use 1/R4.
If we follow the charge field in, we use 1/R. I will solve
another pair of perturbations, to show this in more detail.
Let
us study the opposite effect from Mercury, on the planet Uranus.
Mercury is perturbed from one side, and has very little tilt.
Uranus is perturbed equally on both sides, and has a lot. First
of all, Uranus is the only planet, save Mars, that has planets
larger than itself on both sides. This is important. Even more
important is how the size and distance of these planets create a
balanced field. Uranus has a tilt of about 97.77o,
or about eight degrees from flat, so we would expect fairly
balanced fields on both sides of Uranus. Saturn has a charge
field that is 2.328 times as dense as Neptune's (charge density
differential = mass differential x density differential—see
below for clarification) and is .887 as far away. This gives
Saturn a relative charge density of 2.3281/4
= 1.235. Neptune's is 1/.887 = 1.128. The difference between them
is 4.53%.
4.53% x 90o
= 4.1o. The
first bomb has just dropped. Check your pulse. If not for further
perturbations, Uranus would be tilted to 94.1o.
[We add 4.1 to 90 because 90 is the baseline. 90 is balance, and
we are 4.53% from balance. Zero in this case is not balance, it
is complete imbalance.]
Let us now look at the Earth. You
can immediately see that the Earth is flanked by planets that are
neither close to even nor vastly different. So, given the general
theory, we wouldn't expect zero tilt and we wouldn't expect a 90o
tilt. Let us calculate the actual tilt, straight from the
perturbations. Venus and Mars offset, since their perturbations
are nearly equal. Venus has ten times the charge density of Mars,
but Mars is 1.88 times further away. So if Venus' number is 1.78,
Mars' is 1.88. That is a 2.7% variance, but it is the smallest of
the variances we will find, so we will add it in at the end.
Jupiter has a charge density of 1/1,113 that of the Sun
and is 4.204 times further away. So if the Sun's relative charge
density at the Earth is 5.78, Jupiter's is 4.204. That is a
15.75% variance, or 14.18o.
Saturn has a charge density of 1/7,175 that of the Sun
and is 8.58 times further away. So if the Sun's relative charge
density at the Earth is 9.203, Saturn's is 8.58. That is a 3.5%
variance. But we don't add that directly to Jupiter's angle. We
have to apply that variance to the remaining angle of 75.82o,
giving us an extra angle of 2.65o.
Uranus has a charge density of 1/25,415 that of the Sun
and is 18.23 times further away. So if the Sun's relative charge
density at the Earth is 12.63, Uranus' is 18.23. That is a 18.13%
variance. The remaining angle is 73.17o,
so 18.13% of 73.17o
= 13.27o.
Neptune has a charge density of 1/16,700 that of the Sun
and is 29.1 times further away. So if the Sun's relative charge
density at the Earth is 11.37, Neptune's is 29.1. That is a 43.8%
variance. The remaining angle is 59.9o,
so 43.8% of 59.9o
= 26.24o.
The remaining angle is 33.66o.
We bring in the variation from Mars now, of 2.7%. Which gives us
an angle of 2.43o.
The remaining angle is 31.23o.
The tilt+inclination of the Earth is 30.55o.
I won't continue adding and subtracting influences, since
I have shown the method already (and it gets very difficult after
this). I got more rigorous with each example in this paper, going
from a rough suggestion with Mercury to a fuller list of
influences with the Earth. I will do some more math in part 2 of
this paper, as well answer some broad questions. And in upcoming
papers I will try to do these calculations with absolute numbers,
rather than relative numbers.
I have shown enough math
and examples to strongly suggest my postulate is correct. Now let
me tell you why it works. If the planet has no tilt, the charge
field is coming from one direction. If it is fully inclined, like
Uranus, the charge field is coming from both directions evenly.
Let us look at Mercury first. The
charge field of the Sun is moving mainly radially past
Mercury, since it a simple emission field from the Sun, heaviest
at the equator. If we drew a charge field axis through Mercury,
it would be pointing at the Sun. The magnetic field is orthogonal
to both the charge field and the electric field (due to the spin
on the photons), and Mercury aligns itself to the magnetic field.
Which is why Mercury is nearly straight up.
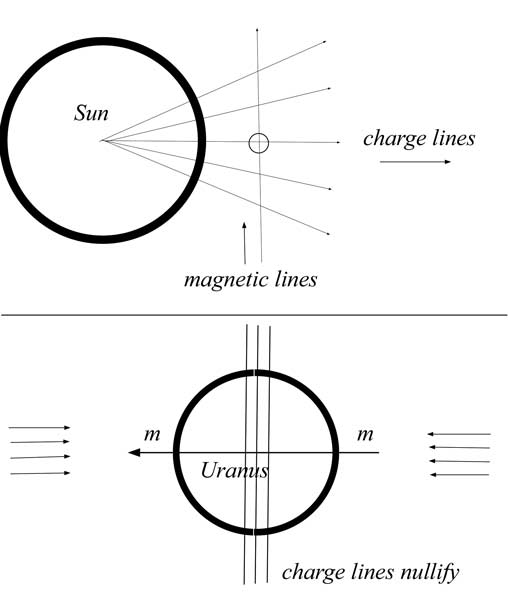
But
a charge field coming from opposite directions evenly, as with
Uranus, becomes a sort of balanced dipole. Although the charge
field is the foundational field underneath electricity and
magnetism, and is normally not a dipole (meaning, it is a
straight bombarding field, or emission field, at the basic level,
as emitted by spheres), in cases like this it does take on a
dipole configuration, since we have bombarding and perturbations
going in two opposite directions. The charge field is
interpenetrable to itself, for the most part, so we can have
charge or photon traffic going both ways in the field. When the
charge field is balanced like this, it creates a sort of zero sum
at the distance of balance. The field lines cancel eachother, and
if we draw them, they no longer have any summed strength in the
radial direction (toward and away from the Sun). Instead, we
would draw them as null, going perpendicular to the Sun. If we
drew a charge or electrical axis, it would be pointing straight
up. But since the magnetic field is always perpendicular to the
charge field and the electric field, and since it is the magnetic
field that guides the real axes, the magnetic axes will line up
with the direction of orbit. Remember from my quantum
spin papers that you have to go orthogonal twice (see the
footnote about the toy dog). So here, to go from Mercury's normal
alignment to Uranus' abnormal alignment, you go 90 degrees, plus
a spin of 1/4 turn.
Of course this illustration is just a
rough visual suggestion, but I think it simplifies the mechanics
into a comprehensible form. I could have also illustrated this
with potentials and pluses and minuses, but I have developed a
distaste for pluses and minuses. What I have here is enough to
begin the revolution.
A doubter will say, “What
makes you think this effect comes from the charge field? You used
mass and density to get your numbers, and we could just as easily
give those to the gravitational field.” First of all,
balanced perturbations from two opposite directions would not
cause a force in the gravity field. I have shown equal
perturbations upon Uranus from Neptune and Saturn. How could the
gravity field cause a turn? Gravity would have to effect the two
poles differently. We can see immediately how charge would effect
the two poles differently, but not gravity. Second, why would you
multiply mass and density in the gravity field? That gives you
D2/V. There is
no possible reason you would square the density of a given
object, and then use that number in the gravity field. But with
the charge field it makes perfect sense. As
I have shown, mass and charge reduce to the same dimensions.
The statcoulomb reduces to mass, and the Coulomb reduces to
mass/second. So if we seek a charge density, we seek a mass
density. Third, the gravity field would not change as I have
shown the charge field changes, as we toward or away from the
Sun. The gravity field never changes at 1/R4
or 1/R, but I have shown the simple mechanical reason the charge
field does so.
Conclusion: I have just shown, with simple
equations, that it is quite easy to explain axial tilt with
unified field perturbations. In fact, the perturbations
themselves are strictly charge perturbations, and I call them
unified field perturbations only because they take place in a
gravity field. To repeat what I have said in many papers, my
unified field IS Newton's gravity field. I
have pulled apart Newton's famous gravitational equation and
found the charge field already inside it. G is the transform
between the two fields that have always been inside Newton's
equation. So all these corrections I am making can be made INSIDE
the existing equations. I am not adding a field to existing
equations, I am showing the fields that were already there all
along. This answers the replies from the mainstream, for a
century, that there was no room for corrections. There is very
little room outside the mainstream or historical equations, it is
true, but there is a lot of room inside them for corrections. The
charge field is inside the existing equations, and it had to be
to make them work mechanically. Celestial mechanics could not
work like it does, with resonances and perturbations and so on,
if it were a single field. This should have been clear to Kepler
and Newton and Laplace and everyone else, but they preferred to
look away.
Now, this is just the beginning, it is true. I
have been forced to use relative math here, meaning my numbers
are one body relative to another. I haven't yet been able to
develop all the equations I need to find numbers straight from
the bodies' masses. Therefore I can't yet publish a full set of
equations to replace those of Laplace. As you can see by my
method here, I could
publish a full set of equations of relative numbers, using the
simple equations above. All I would have to do is keep
calculating perturbations from other bodies, until I had a full
set. Given the number of bodies in the Solar System, that would
be a large set, but it could be done by computers. However, I
prefer to wait until I have the straight equations. These will be
more useful and transparent to current physicists, who aren't
used to dealing with the sort of simple, relative math I am doing
here.
However, I think I have proved my point, made in my
paper on Laplace, that the perturbations should and can be
calculated from masses and distances, without having to write
equations for curves or ellipses. What solves the original
problem of Euler, Lagrange, Laplace, and the rest, is not looking
at the “remaining inequalities,” it is correcting the
mechanics underneath the fundamental equations. Once we do this,
the errors are removed by straightforward means, not by plying
them with differential equations and power series and other
tricks. The same can be said for Einstein's equations. We don't
need non-Euclidean math to solve this, since in perturbations the
charge field is moving in straight lines from one body to the
other. Light may or may not curve when passing large bodies,
depending on what background you choose, but we don't have to
imagine the charge field looping around large bodies in this
problem. The charge photons can go the shortest possible path in
perturbation problems, and that path can be defined as straight.
What I mean by that can be seen by looking at a simple
illustration.
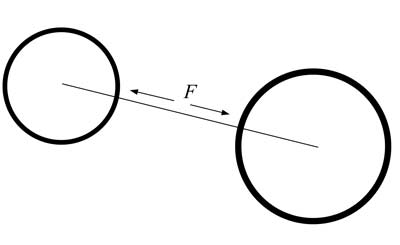
Although
the space may be curved around two bodies (if we want to do math
the way Einstein did it), even then the line between the two
bodies cannot be made to curve. Non-Euclidean math doesn't make
that straight line a curve. Einstein's field equations don't
curve that line. That is the natural line of perturbation,
therefore curved math is superfluous. We can proceed without it.
That is precisely why Newton's equation usually got the right
answer: even in a curved field, his line of influence is
uncurved. Non-Euclidean math doesn't curve Newton's line of
influence, it only adds Relativity or time separation to the
field. Besides that, I have already proved in other papers that
you can add Relativity to gravity without any curves. A Euclidean
math has always been
available to express GR without curves.
Using my new
perturbations, I will eventually be able to dissolve most of the
“inequalities” that remained even after Laplace did
his work. This means that I will also be able to dissolve much of
the “indeterminism” in chaos theory. The Solar System
must be less chaotic once the equations are corrected. Beyond
that, I will destroy the fundamental assumption and presumption
of chaos theory, which relies on the previous perfection of the
equations of celestial mechanics. The universe can only be
chaotic if our equations are perfect. If our old equations were
chaotic, then the universe returns to an unknown, neither chaotic
nor non-chaotic.
Addendum: many have asked why these
charge photons have not been discovered. My answer is that they
have. All the photons we already know about are part of the
charge field. The entire electromagnetic spectrum is the charge
field. We do not have to propose new photons, we can use the ones
we already have. I have given all photons mass and radius, so all
photons must cause mechanical forces by contact. This has long
been known (see the photo-electric effect) but not fully
interpreted.
See
part 2 of Axial Tilt for further clarifications and
equations, including comments on how this solves nutation.
You
may now see the simple unified field equations for the three-body
problem (Sun, Earth, Moon) in my newest paper on Lagrange
Points. Using the charge field, I am able to show that the
Moon is in fact hitting these points of field balance. This
proves my assertions in this paper once more. It also clarifies
the math I do here, since although I run the same field equations
there, they are even more stripped down and transparent.
If this paper was useful to you
in any way, please consider donating a dollar (or more) to the
SAVE THE ARTISTS FOUNDATION. This will allow me to continue
writing these "unpublishable" things. Don't be confused
by paying Melisa Smith--that is just one of my many noms de
plume. If you are a Paypal user, there is no fee; so it might
be worth your while to become one. Otherwise they will rob us 33
cents for each transaction.
|