return to homepage
return to updates
A Critique of
General Relativity
by Miles Mathis
First written November 2004
I have shown in a series of papers that Einstein made many theoretical and mathematical errors in his explanations of Special Relativity. In this paper I will begin my critique of General Relativity.
Relativity has been an important historical step in physics, and this is generally understood, even by non-physicists. Einstein has become one of the most famous people in history due to his contributions to physics, and in many ways he deserves this fame. Although Relativity as he presented it was flawed in any number of ways, and although his method of presentation has caused untold confusion, he is responsible for several real advances. He gave us the first formal theory and math to contain the finite speed of light and many of its implications. He convinced the world of length contraction, time dilation, mass increase, and mass-energy conversion, and supplied us with transforms for all these phenomena that were very close to correct.
All this being said, it is nonetheless shocking to discover the magnitude of some of his errors. Even more shocking is that these very simple algebraic errors have stood for a hundred years under the noses of many famous mathematicians and physicists. I have shown incontestably that the first derivation of gamma is riddled with errors of high-school level algebra, and yet this derivation has never once been corrected or even seriously critiqued. Mathematicians of the first rank, including Russell, Minkowski, Dirac, and Feynman have left it untouched. Since Relativity is math applied to a very complex problem, it is perhaps not surprising that pure mathematicians have not fully penetrated its physical side; but that “towering” mathematical physicists like Bohr, Dirac, Feynman, and many others could not see the errors is astonishing, to say the very least.
In this paper I will begin to show why this is so. My critique of Special Relativity has so far ignored the tensor calculus. Since the space of Special Relativity is flat to begin with, the tensor calculus is not necessary. A Gaussian co-ordinate system is an intrusion in SR. That is why Einstein initially derived his transforms without it. That he could do so is clear—his algebraic derivation is uncorrected by importing the tensor calculus into SR. The tensor calculus does not even fine-tune SR, it only expresses it in a different way. Gamma is the same transform with or without the tensor calculus.
The problem is that Einstein imported the tensors into SR very early in the history of his theory. He did this to impress the top physicists and mathematicians. It worked. But it also had the unfortunate side-effect of cloaking the fundamental level of the theory. SR was only a few years old when the time variable was swallowed up by hyperbolic math. Once that happened, no one cared to look at the old algebra anymore. It was much more fun to play with the new tensors, and top-level scientists and mathematicians of the time would not have been caught dead talking about Relativity in terms of classical variables. They wanted to be heard talking about covariant four-vectors and contravariant tensors of the second rank and Hamiltonians and so on.
Relativity has been buried under the tensors ever since. To this day, no one who thinks much of himself or herself will be caught discussing Relativity without using all the mathematical names and niceties. The tensor calculus is the insider lingo of Relativity, the secret handshake, the esoteric knowledge, the badge of honor.
This social fact has been and remains the number one impediment to improving Relativity. I don’t know that he intended to, but Einstein created a very exclusive club, one that has become frozen in its forms of initiation and its bylaws. The tensor calculus by itself has provided the long apprenticeship, and this apprenticeship has allowed a sort of indoctrination. The years it takes to learn the math become a bridge that no one wants to look back beyond. The past is on the distant shore, and the new master is only interested in the future. Algebra is beneath him, a child’s toy. What is wanted is an ever more complex math with which he can preen himself and fill blackboards.
As an example of this, look at Paul Dirac's lead-in to the tensor calculus in his book General Theory of Relativity [1975]. He says,
One can easily imagine a curved two-dimensional space immersed in Euclidean three-dimensional space. In the same way, one can have a curved four-dimensional space immersed in a flat space of a larger number of dimensions. Such a curved space is called a Riemann space. A small region of it is approximately flat.1
That is his entire explanation of curved space. Afterwards he simply dives into the math. But his foundation is already cracked. First of all, a “curved two-dimensional space” is not two-dimensional. A curved two-dimensional space is three-dimensional, by definition. This mistake should already be a clue that Dirac is long on math and short on conceptual understanding and rigor. And it means that a curved four-dimensional space must be five-dimensional, in which case we need a variable and a variable assignment for this fifth dimension. We get neither from Dirac, and we have never gotten either from anyone else, including Einstein and Kaluza (Kaluza gave us the fifth variable but no assignment of it to any physical or temporal extension). Furthermore, Dirac's last sentence is necessary because he will use the calculus to do math in infinitesimal regions of Riemann space. But you can see that this is a sort of cheat: the mathematician postulates curvature and then ignores it by going to a tiny area where there is no curvature. I will have more to say about that later in this paper.
All this means that I must analyze the theory of General Relativity, the math of General Relativity, and the theory of the math of General Relativity. It will not be enough to analyze the postulates and physical applications of GR. I must also analyze the tensor calculus. Because in many ways, GR is the tensor calculus.
But before I get to a critique of the tensor calculus I want to analyze closely the thought problems that led Einstein into his theory of General Relativity. In this way I will proceed with my analysis in the same order that he did.
The first thing I want to do is critique Einstein's explanation of the spinning disk—his second example in beginning his theory of General Relativity. In The Foundation of the Theory of General Relativity, published in Annalen der Physik in 1916, and the book Relativity, published the same year, he tells the same famous tales. The first is of the elevator car in space. The second is the spinning disk. I agree with his ideas concerning the first, although I don't think he took them far enough. The second tale, however, I do not agree with.
Just to be thorough, I will remind the reader that the elevator car in space showed the equivalence of gravity and acceleration. Einstein showed that without further information it was impossible to decide if an accelerating elevator car was in a gravitational field or not. The vector was theoretically reversible in all ways. In my opinion, this thought problem is brilliantly imagined and brilliantly stated. Einstein only fails to take it to its logical conclusion.
Now we go to the second tale. Einstein gives us a spinning disk, like a merry-go-round, and then does thought transformations on it, to show the affect on measuring rods and clocks. An observer off the disk will see and measure things differently than an observer on the disk. This much I agree with. But his list of observed changes is very faulty.
To begin with, he says that the motion of the disk creates a sort of gravitational field. He says that the observer on the disk could make the claim that he was not moving, saying only that he was feeling forces from a gravitational field. The observer on the disk would feel a force outward from the center of the disk—the centrifugal force—and that the space-distribution of this "gravitational field" would be impossible according to Newton. In a footnote, he says that it would be impossible since, "The field disappears at the center of the disk and increases outward proportionally to the distance from the center as we proceed outwards."
I suppose he means that it would require the force of some massive torus surrounding the disk to explain the field as a gravitational one, and that Newton did not have much use for such things. But of course the reason Newton did not have much use for such things is that none had ever been discovered. I am not aware that any have been discovered since the time of Newton, and so Einstein's footnote is a bit ridiculous. Newton's equations did not forbid the existence of tori, and so I don't see what Einstein's point is. Newton's answer to the observer who claimed to be in the field of a torus would have been, "show me the torus." That is my answer to this footnote.
Notice that the torus would have to be in synchronous orbit around the disk as well, or the observer would see himself moving with regard to it (in which case he could not say he was not moving). If the torus was not in synchronous orbit, the observer could say that it was orbiting him. But in that case he would have to explain why he was feeling no effects from the spinning electromagnetic field of the torus.
More importantly, what Einstein fails to recognize in his example is that an observer riding upon such a disk would be feeling two forces, not one. If he was not flying off into space, he would necessarily be feeling a force of friction, which kept him on the disk despite the centrifugal force. This frictional force would be the one that is analogous to a gravitational field, since the frictional "field" is arrayed around a central point. This would indeed increase with distance, and for that reason alone could not be called gravitational. Gravitational fields, even those of Einstein, diminish with distance. 
All that was admittedly inconsequential compared to what follows. For he now begins his calculations. He says that if we place a clock on the edge of the disk and a clock at the center, then climb off and let the thing spin, we will see (from off the disk) the clock on the edge go at a rate that is permanently slower than the other. This is simply false. For one thing, you must pick a point of view. "Off the disk" is not precise enough. The differences will vary depending on where you position yourself relative to the direction of spin. For instance, I can pick a point where there is no difference in the two clocks. If you let the disk spin in the xy-plane, then draw the z-axis up or down from the center, you can sit anywhere on that axis —no matter how far away—and the two clocks will have the same rate for you. If the disk is very large, then the two clocks will not match up—meaning that the one from the edge will flash the time just a bit later than the one at the center. But this is only because you are closer to the center than to the edge. The periods of the two clocks will be exactly the same. If you are x distance from the edge, then the tick of the clock will be x/c late each tick. But if it is late the same amount each time, then the period has not changed.
Now, what if you are in the xy-plane, like the disk, but you are off the disk? I think this is how most people imagine Einstein's example. Einstein's explanation is still wrong, since I have proven in my correction to SR that approaching objects are not time-dilated, but time-compressed. That is, speeded up. The simplest way to see this is to think of the clocks as waves and then apply the Doppler Effect to them. Receding clocks are red-shifted, approaching clocks are blue-shifted. Therefore, let us say that the edge of the disk that is furthest to your right (D) is moving toward you, and the edge to the furthest left (B) is moving away. The first clock will be speeded up, the second dilated. The clocks at A and C will both be normal—no difference from your clock or from eachother. If the disk is very large and C is very far away, then that time will appear late, but it will not be dilated or compressed. The effects on measuring rods will be analogous. D will look longer, B shorter, A and C will look the same. For this reason, you will not calculate the disk to be a circle. The distance ABC will look shorter than ADC. Points E and F will seem the fastest points to you, since at E the clock is moving directly away from you and at F the clock is moving directly toward you. We could graph a lot of points and draw the blob, but it is not that compelling beyond the points I have enumerated. I believe it would be a blob whose center of area would seem to have shifted forward and to the right, like an egg with its point out from F.
It is clear that I have contradicted Einstein in regard to point D. It is less clear concerning points A and C. I have contradicted his SR analysis of the situation, an analysis he begins his GR paper with. As I said above, he expects all moving points to be time dilated and length contracted. But in equation 71a of The Foundation of the Theory of General Relativity he finds that "with the tangential position, therefore, the gravitational field of the point of mass has no influence on the length of a rod." It is hard to know what to make of this. On the one hand, his gravitational field is not spinning in eq. 71a. On the other hand, Einstein uses the spin in his disk example to create the pseudo-gravitational field. If the disk is not spinning, there is no field. Einstein does not solve this conundrum himself, since he never goes back to the spinning disk to apply his new theory to it. Does General Relativity trump Special Relativity here, or will a spinning gravitational field cause tangential length contraction? Einstein does not say, since he never fully differentiates between his elevator car example and his disk example. He uses them both as lead-ins but does not really solve them. He implies that GR solves them both in the same way, but it should be clear that the disk problem introduces some subtleties that the elevator car, and a non-spinning gravitational field, do not.
My correction to Special Relativity allows us to solve this problem easily, without any tensors. I agree with equation 71a: General Relativity cannot be responsible for any effects at the tangent, whether that tangent is tangent to a gravitational field or to a spinning disk. In my paper on SR, I included a special section on motion at a tangent, and there it is clear that the point on the tangent cannot be dilated or compressed, whether it is moving or not, since it is perpendicular to the line of sight. However, this brings up a further question. Only if the time period or rod length in question is very small will it be unaffected by the experimental situation above. A longer rod or a longer time period will in fact be changed in subtle ways. My claim above, that no dilation or compression will be seen or measured, is true only if the center of the rod or time period is at point A or C. In that case, if we have a rather long rod, then the "half" that is before C will be slightly shorter and the half that is after C will be slightly longer. This is because a y-component of the first half of the rod will be fleeing the observer, and the y-component of the second half will be approaching. The same, in reverse, applies to the time period.
But if you have a rather long time period that starts at point A or C, then it must be compressed or dilated, since as it moves away from A or C it will develop a y-component relative to the observer. This y-component will be affected, and it will be affected more the longer it continues beyond point A or C.
It is also worth noting that all these rods will be not only stretched or compressed, they will also be curved. The y-components and x-components of the stretching or compressing will not be proportional, so that the rods will look bent from off the disk.
Now that we have cleared up that subtlety, let us move on. It is clear that I agree with Einstein’s main point that the circle described by the disk in its own field will not act like a circle if measured or viewed from outside that field. Our observer will not see a circle, as I admitted. Therefore we require transforms. So far I have only disagreed with Einstein’s analysis of specific changes in the fields. But now we must look at one of his main claims regarding the motion of objects, or of light, in accelerated fields. At the end of section 2 of The Foundation of the Theory of General Relativity, Einstein says this: “The path of a ray of light with respect to K’ must in general be curvilinear, if with respect to K light is propagated in a straight line with a definite constant velocity.”
He came to this conclusion via the disk example. All points on the disk are feeling a centripetal acceleration; therefore they are in a sort of gravitational field. Now, if we turn the disk into a merry-go-round and put a child on a horse on the periphery somewhere, and let that child throw a ball to the stationary observer, then the observer sees the trajectory as a straight line. The child sees the trajectory as a curve. The same basic analysis applies to the elevator car in space. However, there is one subtlety of this problem that Einstein has missed. Both the child on the horse and the man in the elevator car are in real motion relative to the observer and to the field itself. To see what I mean, let us look at the man in the elevator car. He is either in an elevator car that is accelerating upwards or is at rest in a gravitational field centered below him. If he is accelerating upward then he will see light (and all other objects that move in straight lines external to his car) as curved. But if he is at rest, then we must ask why he is not falling toward the center of the field. The bottom of the car must be supported by some solid structure. If so, then we must change his description: he is either feeling one constant force up, or he is feeling two constant and equal forces, one up and one down. What he is not feeling is one constant force down. If he were feeling one constant force down, he would be moving in that direction. This constant force down would be the force of the gravitational field acting alone, without any structure to resist it. We know he is not in this situation because if he were he would not be stuck to the floor of the elevator car. Einstein says that he is stuck to the floor. If he and the elevator car were in freefall, then he would be floating just above the floor of the car.
The problem is that this last situation is the only one that GR finds equations for. GR calculates accelerations at different points in the field. But Einstein’s elevator car does not fit this situation. It is not falling freely in a field. It is at rest in a gravitational field. This is important because a body at rest in gravitational field and a body falling freely in a gravitational field do not see light in the same way. A body falling freely is accelerating, and therefore Einstein is correct to say that it would see light traveling in a curve. But a body at rest in a gravitational field would also be at rest relative to any external field. Therefore it would not see light travel in a curve.
This means that Einstein’s quote above is false. It would be true only if it read, "The path of a ray of light with respect to a body accelerating in K' must in general be curvilinear, if with respect to a body in K light is propagated in a straight line with a definite constant velocity." This is because, if I am standing on the earth and the earth is K’, I may be feeling a force of gravity, but I am not accelerating due to that force. If I am not moving with regard to K’ and K’ is not moving with regard to K, then I am not moving with regard to K. There is no reason for me to see incoming light as curved. I would see incoming light as curved only if I were in freefall.
This is a critical error for Einstein, since he uses the sentence above to justify all kinds of things. He treats it as proved and then considers it an axiom. A false axiom of this magnitude is difficult to overcome without a lot of mathematical tricks. Unfortunately, as I will show, the tensor calculus provides Einstein and others with a nearly bottomless bag of tricks.
Einstein's next step is to ditch Euclidean space in favor of Gaussian co-ordinates and the tensor calculus. But I have not seen any good argument for doing so in any of his writings. Gauss' method only works if "sufficiently small areas under consideration act as Euclidean areas," as Einstein admits. I consider this in itself a theoretical reductio, since the Gaussian method is a method of infinitesimals, and the field must be considered Euclidean at the infinitesimal level. If this is true, then the method cannot be said to apply to non-Euclidean systems, except as a kind of fudge. Nor do I see why it is necessary that the gravitational field be non-Euclidean in the first place. Einstein's examples of the elevator car and disk do not lead in that direction, although he implies that they do. He says "it is not possible to obtain a reasonable definition of time," with regard to the disk or any other gravitational system using flat fields. But I can easily offer a reasonable definition of time with regard to any system. A rotating system is no different than any other system. I will show that transformation equations are quite easy to come by (although the equations increase in number), and I can offer a definition of simultaneity as well. Just as I showed with Special Relativity, some observers will be privileged, by utilitarian considerations which can be proven once again by Doppler shifts.
Furthermore, the tensor calculus introduces a margin of error into all calculations, as shown by Einstein's inclusion of Appendix II in The Meaning of Relativity. Although this imprecision is more widely known as the "strength" of various field equations (depending on the "free data" in the system), in my opinion this imprecision or margin of error is just that. It is caused by treating the field as non-Euclidean and then applying infinitesimal Euclidean math to it. Since gravity is believed to be a force acting over large distances, and is treated by General Relativity as such, it is absurd to apply to it a math that only works well in small sub-areas—areas where gravity is not even applicable.
In section 4 of The Foundation of the Theory of General Relativity, Einstein says, "For infinitely small four-dimensional regions the theory of relativity in the restricted sense is appropriate, if the coordinates are suitably chosen." This means that SR applies at the limit, and that the gravitational field becomes flat at the limit. But of course if the field is flat or rectilinear at the limit, then the gravitational field does not exist at the limit. It is difficult to see how we are going to find equations for the gravitational field by going to a limit where it does not exist.
This is where we must look very closely at the fundamental assumptions of the tensor calculus. I have shown that the regular calculus has historically proceeded by a compensation of errors and by following the diminishing differential instead of the constant differential. The tensor calculus followed Newton in assuming that a curve could be straightened out by making it appropriately tiny. Einstein had no reason to question this assumption. But in fact, it is a false assumption, both for the regular calculus and the tensor calculus. The derivative equation is derived not from going to a limit but from going to a sub-interval. The derivative is not a variable at an ultimate or infinitesimal interval. It is the change in that variable over a subinterval of 1.
Now, it is true that the tensor calculus mostly works, and it mostly works for the same reason the regular calculus mostly works: the derivative equation, although wrongly derived, is a correct equation. It gives us the right numbers. But the tensor calculus is conceptually sloppy in exactly the same ways as the regular calculus, and then some. For example, the regular calculus has taken a lot of heat historically for sometimes treating the variables at the limit as zero and sometimes treating them as very small quantities. The tensor calculus does the same thing. Let’s look at Einstein’s derivation of his fundamental tensor. He starts with this equation:
ds2 = -dx12 – dx22 – dx32 + dx42
This is the famous four-vector equation he inherited from Minkowski. Obviously, none of these vectors can be zero. They are only very small. In fact, they must not be zero. If ds is zero, then we cannot calculate solutions.
Some pages on, at the beginning of section 8, we get this equation:
ds2 = gμν dxμ dxν
Once again, these infinitesimals cannot be zero. They must not be.
But in equation 18a of section 8, Einstein gives us this:
dτ0 = √-g(dτ)
Where τ is the volume. And says, "If √-g were to vanish at a point of the four-dimensional continuum, it would mean that at this point an infinitely small 'natural' volume would correspond to a finite volume in the co-ordinates. Let us assume this is never the case. Then g cannot change sign….It always has a finite value." This means that the infinitesimal values must be zero. If they have no finite value then they must be zero. There is no third choice. Even Newton and Cauchy understood this. The epsilon delta proof understands it. Newton said, in effect, "any value you can name, I can name a smaller one: that is all that is necessary to my proof. My value is smaller than yours but it is not zero." The epsilon delta proof mirrors this argument with a bit more rigor. And yet the tensor calculus and Einstein proceed by disallowing the volume at the limit from having any finite value.
In one place in the proof ds must not be zero, at another dτ must be zero. The tensor calculus, just like the regular calculus, cannot decide whether the infinitesimals have extension or not. They must have extension in the math, they must not have extension in the physical field.
Another thing is curious here, and I cannot pass it by without comment. The very next equation in Einstein’s text is this one:
Eq.19: |dx’σ/dxμ| = 1
This is found by letting √-g = 1, so that dτ’ = dτ. This is extraordinary, because if the volume of every infinitesimal is equal at the limit, then that means that everything is equal at the limit. Time and distance must be equal at the limit, which means that space is homogeneous at the limit. Not only is the field rectilinear at the four-vector limit, it is non-time-dilated and non-length-contracted and non-mass-increased. Einstein admitted above that SR works at the GR limit, meaning that the field is Galilean and Euclidean at that level. But he has not taken his analysis far enough. Volumes are not equivalent in SR, since lengths are not equivalent. Therefore his GR field at the limit must be an absolute. He almost admits this when he says, “The invariant √-g(dτ) is equal to the magnitude of the four-dimensional element of volume in the ‘local’ system of reference”.
I draw your attention to that word “local”. He clearly has in mind what I have called the local system, which is the system measured locally, from no distance. Feynman also makes use of the local system in trying to explain some of the subtleties of Relativity. By using the two words “local” and “invariant” in the same sentence, Einstein has come as near as he ever did to the word “absolute”. He might as well have admitted it: according to the tensor calculus space is absolute at the limit. Meaning that it is invariant in every way. All local time and distance is equivalent, invariant, and absolutely equal to all other local time and distance.
I don’t agree with his math, but I agree with his postulate. All local time and distance must be equal in order to measure relative differences. If you do not postulate local invariance you cannot derive transforms at all, neither in SR nor in GR. But of course this is extraordinary because it contradicts the current interpretation of Einstein, which insists that the local field does not exist. The standard interpretation likes to believe that Einstein somehow derived his transforms from nothing. It likes to insist that Relativity has no absolute postulates, except for the speed of light. It likes to insist that there is no absolute space, even at the limit, since this would seem to imply an ether. Nothing is more passé than the ether. I am not arguing for the reinstatement of the ether, but I think it is clear that we must postulate the equivalence of all local time and space, as I defined both of these in my SR papers. And I think it is clear that Einstein admits this, in his own way, precisely here.
I have shown2 that the reason this must be true is that making the speed of light absolute determines, by itself, that the local field must also be absolute. The two postulates are equivalent. If you assume that light is a constant, you must also assume that dt and dx are constants. That is to say, the local field is invariant. The speed of light is a clock setter. It is also a length setter.
Perhaps the best way to show that the tensor calculus is superfluous is to simply solve a GR problem without it. The first problem Einstein solves with his new math and theory is the refraction or aberration of starlight by the sun. He has already posed as an axiom the fact that light moves curvilinearly in a gravitiational field. Now he only needs to calculate the amount of curvature in a real field.
I will calculate in a completely different way. I dismiss his axiom as unproved. I do not accept that light must travel curvilinearly in a gravitational field, except under certain conditions. It will appear to travel curvilinearly to an observer in freefall or in orbit. We here on earth observing starlight passing the Sun are in a sort of freefall relative to the gravitational field of the Sun, so we would see starlight curve. But in this case, it is the acceleration of the Earth that makes the light appear to bend, not the pull of the Sun on the light. If you could stand on the Sun without burning up, you would be at rest relative to the central field and would not see starlight curve. The curvature of starlight is relative to position. It is not absolute, even within the field. It cannot be treated as an axiom. Therefore I must solve in a completely different way.
To develop my method, we must return for a moment to the problem of the disk. Let the disk again be a merry-go-round, and let a child be on a horse on the periphery of the spinning ride. This child wants to throw me a ball. He can easily do so, and I will see the trajectory as a straight line. But the child will see the trajectory as a curve, provided he defines himself as stationary. This is all that Einstein means, or can mean. Replace the ball with a photon, and the child calculates that it has taken a curved path. But, once again, I calculate that it has arrived at my eye in a straight line.
Obviously we have two choices in developing transformation equations here. From the point of the view of the child, we need a math that describes curved lines. From the point of view of the parent standing off the ride, we don't. We can use pretty simple math. But once a transform is arrived at, it will work in both directions. All we have to do is reverse it. So of course we should choose to develop the transforms from the point of view of the parent.
Einstein claims that this is not always possible. There is not always a point of view that can be found where the paths of the light rays are straight. He gives as an example the gravitational field of the sun. There is nowhere one can go, he says, where one can calculate with straight light paths; therefore we need a new highly complex math. But this is simply not true. One may or may not be able to carry oneself physically to a place in space where the light rays passing the sun will appear straight, but one can easily carry oneself there conceptually. Just imagine that the sun is expanding at a constant rate, one that would perfectly offset the curvature of the light path. Then develop the transforms, and afterwards reverse the direction of the acceleration. You can do simple Euclidean math, meaning algebra, to describe the field, and then reverse it. You make all the acceleration vectors point toward the sun, instead of away from it. The field itself is exactly the same either way. If I am accelerating toward you, you are accelerating toward me. This obviates the need for curvilinear math altogether. And Einstein's own equivalence principle is what gives us permission to do this!
Besides, the reason we cannot carry ourselves physically to a point where light does not curve relative to the field of the Sun is an experimental reason, not a theoretical reason. Meaning that if we could bear very high temperatures, we could go stand on the Sun and see light without curvature. In fact, in a slightly different case, we could actually do the measurement. Einstein calculates a bending of starlight by Jupiter, predicting .02 arc seconds. Well, we could land on Jupiter and see the light unbent by Jupiter’s field there. On the surface of Jupiter, we would be at rest relative to Jupiter’s gravitational field. We would not expect to see a bend of .02 seconds of arc from that position.
Just think of the operator of the merry-go-round. If he were standing in the very center, and if he were not rotating, then he would not see the ball thrown off the ride as curved. He would see like the parents, not like the child.
Even from the point of view of the child on the merry-go-round, I do not see the need for tensors. Einstein says that Euclidean math cannot be used since no Euclidean space can be found in a gravitational field from which to measure the curvature. There is no orthogonal space underlying the curved space. But this is simply false. It is false since curvature necessarily implies a relation to a non-curved background. The meaning of curvature is absolutely dependent upon the existence of a straight line. If the child on the merry-go-round sees a ball thrown off the ride—or calculates a photon emitted—to travel a curved path, he must see it with regard to a Euclidean background. That background is in fact the "space" of the parent off the ride. If the space of the parent were also curved, then the child could not see any curvature. Motion, whether linear or curved, is always defined relative to a background. A curve in curved space is not a curve.
As proof of this, we know that starlight is refracted only by referring it to some Euclidean system. It is curved relative to the background we apply to it in order to see how curved it is. If the ray is refracted some measurable quantity, we know this quantity only by referring it to the path the light would have taken if the field of the sun were not present. This reference field of measurement is precisely the Euclidean field I am talking about. Whether it exists in reality is not pertinent. It can be made to exist as a concept, and indeed it must be in order to measure the degree of aberration of starlight. This field is the field we should choose to do our math in, since it is a Euclidean field and requires no esoteric tensors or slipshod concepts. In fact, the curvature of the light defines the field at that radius. Since a gravitational field is not dependent upon the mass of the test particle, a photon will do as well as any other test mass. But again, the curvature or strength of the field could never be measured without referring it to the path a light ray would have taken without the gravitational tug. That is, a straight light path. This straight light path is precisely the orthogonal field we require: it is the Euclidean space underlying every non-Euclidean field.
I have proved this beyond a doubt in my paper on aberration, where I found the same number for aberration near the sun as Einstein, using only one simple algebraic equation. In comparison, let us look first at Einstein’s math. In 1911, he provided this equation in his paper On the Influence of Gravitation on the Propagation of Light:
a = (1/c2)∫(kM/r2)(cosθds)
where a is the aberration and the integral is taken from θ = π/2 to θ = -π/2.
This equation took him pages of complex math and theory to derive. Unfortunately, it gave him .83 arc seconds, a number that history has conveniently forgotten.
In 1916, in The Foundation of the General Theory of Relativity, Einstein gave us this equation [eq. 74]:
B = ∫(∂γ/∂x1)(dx2)
Where B is the aberration, the integral is taken from +∞ to -∞, and
γ = √(-g44/g22)
So we have an integral of partial derivatives, one of which is the transform gamma expressed as the square root of the negative ratio of two tensors. This equation took him 50 pages of math and theory to derive. From all this Einstein gets the number 1.7 arc seconds.
I get the same number from this equation:
θ = tan-1(gt2/2)/d
Where g is the acceleration of the earth and d is the distance to the sun. I derived this equation simply by turning all the acceleration vectors due to gravity around. Rather than have the acceleration vector g point at the center of the earth, I turned it around and had it point from the center of the earth outward. Conceptually, this had the effect of making the earth actually accelerate spherically. Mathematically, it had no effect at all beyond flattening out the field. Turning the acceleration vector around made the field a Euclidean field, a field I could do simple math in. Once I achieved my number for aberration, I could leave the vector turned or put it back to the way it was. If I put it back the way it was, I return to a curved field. But my number is the same either way. Just look: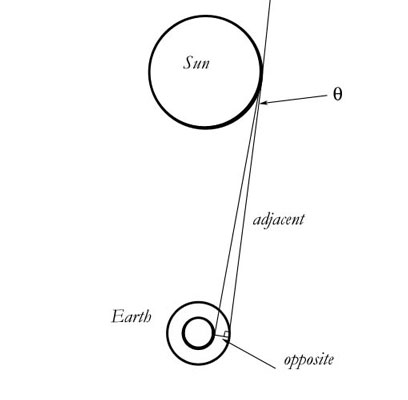
opposite = s = gt2/2
t = time for light to travel from the tangent of the sun to the earth
= light time from sun to earth + light time of the radius of the sun
s = (9.78 m/s2)(501s)2]/2
s = 1,230,000m
tanθ = opposite/adjacent
tanθ = 1,230,000m/1.51 x 1011m
θ = 1.68 seconds of arc
To see why this number does not match the current number 1.75, go here. I show that gamma causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.
You will say that I have ignored the gravity vector of the sun here, which is the main vector. But I showed in my previous paper that the operation of measuring aberration allowed us to ignore the sun’s field. If we turn the sun’s vector around in the same way we did the earth’s, then the sun will be expanding after the light has already passed the tangent. We do not care what happened before the light reached the sun, since the aberration did not take place then. We care what happened after the light reached the sun. But if we have turned the vector around in order to flatten out the field, then the expansion of the sun cannot affect the light. It seems odd, but it is the field of the earth that causes aberration, once the vectors are reversed.
You tell me which equation you would rather teach to students, or supply a full derivation for, or develop a theory to contain. The so-called free data in Einstein’s equations is considerable. There isn’t a speck of free data in my equation. My “field strength” is 100%.
No doubt you will say you would prefer to teach an equation that is correct. But my equation is correct. It gets the right number. Modern mathematicians have been famous for claiming that you can apply any math you want to a problem, as long as you do it in the right way. And they are correct. Minkowski answered his critics by saying that his fields were a mathematical convenience: he did not need to prove their physical reality, he only needed to get the right answer. In this, he was right. Any math that does not contain false postulates is as good as any other math.3 But modern mathematicians have used this as an excuse for test-driving all sorts of esoteric maths. I turn the tables on them by showing a simple algebraic solution, in a Euclidean field, that undercuts their tensor calculus.
I have achieved the ability to calculate in Euclidean fields by making a single change: I have turned all acceleration vectors around. Simply reversed them. Einstein himself gave me the ability to do this. I am not contradicting his theory, I am just interpreting it in simpler language and math. The vector reversal is a direct outcome of the equivalence he spent so much time proving. His elevator car in space showed us that mathematically there is no difference between “gravity down” and “acceleration up.” If this is true, then there is nothing stopping us from assuming the earth is accelerating up. We assume it just to do our math and then drop the assumption afterwards if we like. It is a mathematical convenience and nothing more, precisely like the convenience of i (except that my simple math is a lot more convenient than i). This is what “equivalence” means: it means that the two situations give us the same number. In developing equations, we are seeking numbers, nothing more. We can house those equations later in any theory we like. If “gravity down” and “acceleration up” are mathematically equivalent, and “acceleration up” gives us a Euclidean field wherever we want it, why should anyone prefer non-Euclidean math? Only a show-off would prefer fifty pages of calculations where he could get by with one page.
After all this, I have come to the conclusion that the Gaussian field and the tensor calculus were imported by Einstein for reasons that are strictly ones of public relations. They are impressive in their own right, in the way of all esoterica, and I think it is fair to say that the math of General Relativity is as famous as the theory itself. Einstein's genius is that he chose just the right gown in which to dress his theory for the ball. An avant garde math was sitting around just waiting to be asked out by some ambitious theory, and Einstein had an eye for such matchmaking. Neither the field nor the math were really necessary to an updated theory of gravity, but Einstein worked very hard to make them seem so. He created an incredible amount of confusion, in part by infusing into his writing a mishmash of German philosophy and big, imprecisely used words (like epistemology), in part by writing in a very opaque style—a style that was and is a commonplace in science writing. This faux-haut style fooled most of his fellow scientists of the time. Where a truly learned discourse would have sent them running for cover, or simply confused them, a stilted sentence structure with a quasi-mystical lilt thrown in now and again was just enough to impress. In the case of General Relativity, it was sufficient to obscure the straightforward nature of the problem at hand and to seem to recommend the equally obscure math of Gauss in order to solve it. Not as much new confusion was necessary with General Relativity as with Special Relativity, since the reader was still reeling from all the murky sentences and murkier equations of the latter and therefore did not need many new clouds in his sky. Besides, most of the obscurity of GR would be provided by the tensor calculus.
Some feminists have recently tried to establish Einstein's first wife Mileva as an equal partner in his triumph if not his fame, and it may well be so. If it is, then she bears equal responsibility for the disaster of the tensor calculus, since, from what I understand, it was she who first recommended it. She was the professional mathematician. It may be that she was the one who saw the PR possibilites. However that may be, it seems fair to say that it was Einstein himself who thought to rewrite Special Relativity with the tensor calculus in order to make it shine at Princeton. This seems proof beyond anything that the math was used as the primary selling point, since there is no other argument that can be made for using the tensors to solve SR. If the argument for making GR a Gaussian field is tenuous, the argument for making SR one is non-existent. Einstein has already stated that the SR field must be Euclidean and Galilean, by definition. It can therefore hardly benefit from the imprecision (free data) and unwieldiness of matrices and field equations.
For much more on this problem, you may now visit my multi-part analysis of the Einstein field equations, which revisit this problem in finer detail, including a line-by-line critique of Einstein's 1916 paper.
1Section 5, paragraph 1
2See section 8 of my paper on Special Relativity.
3Minkowski’s math contains several false postulates, as I show elsewhere. It contains the false postulates of Einstein (like x = ct) and it adds to them the false postulate that time travels at a right angle to x, y, z.
Go to my correction of the perihelion precession of Mercury
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.