The Extinction of π
the short version
by Miles Mathis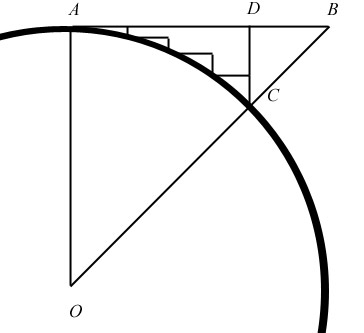
Go to original version
Given the diagram above, which is part of a circle, we let
AO = AB
This makes the angle at B equal to 45o. Which means that
DB = DC.
This must mean that, by substitution,
AD + DC = AB
Now, the distance AD + DC can be redrawn as any number of sub-distances, as above.
Here we divide the distance into four sub-distances, taking us from A to C in 4 steps.
This new path, drawn by the sub-distances, is equivalent in length to AD + DC, as can be seen by any cursory analysis. It is nearer the path of the arc AC, but it retains the original distance of AD + DC.
If we divide the distance into eight sub-distances instead of four, we approach the path of the arc AC even nearer; but, again, we retain the original distance of AD + DC.
If we take this process to its limit, we take our path to the path of the arc AC.
This must mean that the length of the arc AC is equal to the distance AD + DC.
By substitution, this means that
arcAC = AB
Since 8 such arcs make up the circle, the circumference of the circle is 8AB.
Since AB = AO, and AO is the radius, we have found that
C = 8r
π does not exist in the circle equation. It is extinct.
Some will say this is just doing the calculus wrong, but I claim that history has done the calculus wrong, not me. The common answer to my demonstration above is that at the limit, defined as it currently is, the total length of the steps never approaches the arc, because even with a very large number of steps, the distance between each step and the curve remains real. We can sum this distance even at the limit, keeping the sum of the steps above the sum of the curve. It is not the sum of the steps that approaches the curve, it is the curve that approaches the chord. In other words, it is the hypotenuses of the little triangles that converges upon the curve, not the sums of the other legs of the triangles.
While I recognize that this is the common interpretation, I cannot agree with it. In my paper on Newton's lemmae, I proved that the tangent in his triangle must be longer than the chord and arc at the limit. If we apply that to this problem, it means that the arc cannot approach the chord at the limit. The tangent is a component of the arc, by Newton's own definition of it in the Principia, so if the tangent is longer than the chord at the limit, the arc must be also. This means that the curve does not approach the hypotenuses of these steps, no matter how many there are. The hypotenuses are the chords, and they cannot be approached by the arc or tangent.
You will now ask where in the Principia Newton says that the arc is composed of the tangent. It is where he tells us that the orbital motion is composed of the centripetal acceleration and the innate motion of the body. These two vectors compose the orbital motion. They are the only two motions given us by Newton, and he explicitly assigns the innate motion of the body to the tangent.
This means that the historical and current interpretation cannot be correct. The hypotenuses do not converge to the curve or the arc. No, as I show above, it is the tangent that converges upon the arc, but the convergence happens only when the tangent equals the radius. This convergence can happen only at 1/8th of the circle, and it happens just as I show in these papers. It happens because the arc is never a continuous curve, even at the limit. The arc is defined as a curve composed of linear or straight vectors, therefore it can never be continuous, if we mean by continuous that the time or length traveled goes to zero. Logically, the time or length cannot go to zero, since there is no time or length at zero. All numbers in math and physics imply a differential, and since this is so, the curve cannot be thought of as continuous in this way. The curve must be thought of as composed of linear vectors, even at the limit. And since this must be true, it must also be true that the path I have drawn above must converge upon the arc, for precisely the reasons I have stated. The path does converge upon the arc, in the sense that the path gets nearer the arc. No one can deny that, at least. But since the arc is not continuous even at the limit, the path truly does converge upon the arc, as we draw more steps. Since the distance doesn't change no matter how many steps we draw, the tangent must converge upon the arc. Or, at 1/8 of the circle, the tangent simply IS the arc.
For those of you who have read Dan's critique of this paper at ex falso, you might want to go here for the rebuttal. I didn't write it, since I find that the arguments at ex falso pretty much fall apart on a first reading, without the need of any rebuttal from me. [I will say that addressing this short version instead of the long version was a sad misdirection on the part of ex falso. Why would you critique a gloss when a full version exists and is available to all?] And I don't know who did. I only know the moniker Sleestak from my youtube page, where Sleestak is one of my subscribers. And I had thought he was there to hear me sing!
go to long version
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.