|
|
return
to homepage
The
Extinction of π
by
Miles Mathis

bye-bye
π
If you get lost at any point in this paper
you may
go to the short version
First
posted September 9, 2008
Abstract:
I show that in all kinematic situations, π is 4. For all those
going ballistic over my title, I repeat and stress that this
paper applies to kinematic situations, not to static or geometric
situations. I am analyzing the equivalent of an orbit, which is
caused by motion and includes the time variable. In that
situation, π becomes 4. I will also remind you this is not just
a theory: it has been indicated by many mainstream experiments,
including rocketry tests and quantum experiments (see links
below). It has also now been proven by my own experiments (see
link below).
[May
1, 2018:
This paper has now been up for almost ten years. In that time, it
has become somewhat overgrown with addenda and other links, which
I have added as my argument has advanced. Readers soon found
confirmation wherever they looked, and I have added those links
to bolster my thesis. I have made some effort to clean up the
paper recently, though most will still find it to be—how shall
I put it—overrich. It is a long and complex question, and as
usual I have been exhaustive in researching it. One critic called
this paper “discursive”, though he doesn't seem to know what
the word means. Nothing I say below is off-subject or digressive.
The problem of π touches on many other questions, and can't be
discussed in any depth without hitting those questions at some
length.
Whatever
these planted critics may be paid to say, the subject is now
pretty much settled. No one who studies my arguments can fail to
recognize that I discovered something very important here, so we
must assume the people trolling me on the web are agents of some
sort, wasting our time with low-level debating tricks. In the ten
years this paper has been up, I have yet to see a reply or
debunking worth addressing.** None of them even appear serious on
the surface, and none are from recognized people in any field.
Most are from anonymous sources. This is to be expected, I
suppose, since it is difficult to debunk something that is
obviously true. The standard method of debunking the truth—the
method we see at places like Snopes, for instance, or other
mainstream spook fronts—is with low-level character
assassination, couched lies, and other oily subterfuge. We have
certainly seen that in the mainstream response to me from the
beginning, but we have seen little else. I am only telling you
this because Google seems to be in on the game. Any search on me
is littered in the first pages with this misdirection, and
someone who didn't know any better would assume I really am
widely considered to be a crank. I'm not, as you can see here.
Probably more of my papers (on both sites) have gone viral than
the papers of anyone else in history, though you have to dig a
bit to figure that out. My science papers are being mobbed by
mainstream physicists as well as by interested amateurs,
including this paper. In fact, I have it from inside sources that
the mainstream has already begun correcting its kinematic
equations that include π, though they are of course not publicly
admitting it. Apparently they are trying to figure out how to
proceed without giving me any credit. What they don't understand
is that it doesn't matter: I know and they know and they can't
change that. They can't suck the information out of my head or
their own heads, and those are the heads that determine this.
Even if they somehow succeed in stealing this from me, they will
always know
they stole it. That won't make
things better for them, it will make things worse. The only hope
for these people is coming clean, and we can only hope they
eventually figure that out. As I have said many times, if they
start playing nice, so will I.]
[September
24, 2016: There
is now a simple experiment
posted on youtube by a Dutch engineer, one of my readers,
showing π=4 when motion is involved. To go with the arrival of
that experiment, I have published another short
paper on the subject, which stands as a further
simplification and may be easier to penetrate than the analysis
below for most people. You may also consult my
recent paper on the cycloid for further clarification and
simplification of the problem.]
I suppose I
shouldn't be surprised this paper has ruffled feathers. It was
meant to. I made my title provocative on purpose, so it is no
wonder it has succeeded in provoking. You don't promote a
revolution in science with meekness, and no one has ever accused
me of being meek. They have accused me of a lot of things, but
never that. I saw very quickly that, beyond my main thesis, I
could counter all the pi-dolatry
on the internet with this paper, and of course I embraced that
with my usual fervor.
That said,
before we get started let me answer a couple of prejudices. Many
readers, especially those just coming to my papers, will hit a
wall at some point in this paper. No doubt many already hit that
wall when they read the title. Understandably, π as 4 is a big
pill to swallow. This is admittedly one of my most difficult
papers to absorb. It alone is a huge red pill, and will start you
on a journey far more fantastic and interesting than any Matrix
movie. Beyond that, this paper cannot stand alone. It is a
mistake to start with this paper. Those who do start with this
paper will very likely be led to believe I am simply doing the
calculus wrong. To these people, I say that it is not I who am
doing the calculus wrong. It is Newton and Leibniz and Cauchy and
everyone since who has been doing the calculus wrong. I have
earned the right to write this paper by first writing three
important papers on the foundations of the calculus. The
first shows that the derivative has been defined wrongly from
the beginning, and that the derivative is a constant differential
over a subinterval, not a diminishing differential as we approach
zero. There is no necessary approach to zero in the calculus, and
the interval of the derivative is a real interval. In any
particular problem, you can find the time that passes during the
derivative, so nothing in the calculus is instantaneous, either.
This revolutionizes QED by forbidding the point particle and
bypassing all need for renormalization. The
second paper proves that Newton's first eight lemmae or
assumptions in the Principia
are all false. Newton monitors
the wrong angle in his triangle as he goes to the limit,
achieving faulty conclusions about his angles, and about the
value of the tangent and arc at the limit. Finally, the
third paper rigorously analyzes all the historical proofs of
the orbital equation a=v2/r,
including the proofs of Newton and Feynman, showing they all
contain fundamental errors. The current equation is shown to be
false, and the equation for the orbital velocity v=2πr/t is also
shown to be false. Those who don't find enough rigor or math in
this paper should read those three papers before they decide this
is all too big a leap. I cannot rederive all my proofs in each
paper, or restate all my arguments, so I am afraid more reading
is due for those who really wish to be convinced. This paper
cannot stand without the historical rewrite contained in those
papers, and I would be the first to admit it.
[Added
December 10, 2012:
after an email from a reader concerning the
Taxicab geometry, it dawned on me that Hilbert's metric is
basically equivalent to my "metric" in this paper. In
Hilbert's metric, π also equals 4! And it equals 4 for the same
basic reason π equals 4 in this paper: my "limit" is
approached in the same way his is. See below, where I show the
approach to the limit using circle geometry. Well, Hilbert uses
the same sort of analysis. Only difference is, I dig a bit deeper
into the kinematics, showing the real cause of the problem. At
Wikipedia, they say the difference in metrics is caused by
single-axis motion:
This
is essentially a consequence of being forced to adhere to
single-axis movement: when following the Manhattan metric, one
cannot move diagonally (in more than one axis simultaneously).
But
that isn't the cause. The cause is the motion itself. The motion
brings the time variable into play, which adds another degree of
freedom to the equations. You may now consider the fact that
contemporary physicists often use the Manhattan distance or
metric when they get in a jam, especially at the quantum level.
The Manhattan metric is the same as Taxicab geometry. And you can
now understand why using this metric helps them: as I show in
this paper, standard geometry fails because it fails to include
the time variable explicitly, which fouls up the math and then
the physics. In kinematic situations like the orbit, the correct
math and physics includes the analysis I provide in this paper,
in which π=4. And this means that all the hotheads** on the
internet going ape over my paper now have to take on Hilbert as
well. I don't esteem Hilbert and never have, but in this case
having him as an ally is a considerable boost. The mainstream
esteems him, often more than Einstein or Newton, it would seem.
So if my proposing π=4 automatically qualifies me as a crank or
crackpot, these critics will have to explain why the same does
not apply to Hilbert. Is Hilbert a crackpot for proposing that
π=4?
Also of
considerable interest is the fact that in Taxicab geometry, the
circumference is 8r, as I show in this paper. Furthermore, all
this also connects to my
earlier corrections to a=v2/r,
where I show that the denominator should be 2r rather than r. The
same thing would be found in Taxicab geometry, by extending the
equations just beyond where Hilbert took them. To read more on
this, you may now consult my
latest paper, where I extend my comments of this section and
offer some more diagrams and animations, including a video on
youtube produced by Caltech.]
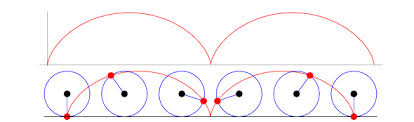
a cycloid as
created by a surveyor's wheel
[Addendum
April 2014. Another
reader has now helped me add to this proof, since she has
reminded me that the arc of a cycloid is also 8r. That is, in the
cycloid, π is replaced by 4, just as in the Manhattan metric. I
don't know why I didn't think to include this before, since it is
so obvious. We should have always asked more persistently why the
arc of the cycloid is 8r while the circumference is 2πr. As a
matter of kinematics, it makes no sense. The same point draws
both, so why the 21% miss? I will be told that it is because with
the circumference, the circle is not moving along an x-axis, but
with the cycloid, it is. It is the difference between a rolling
circle and a non-rolling circle. It is this lateral movement that
adds the 21%. But whoever is telling me this is missing a very
important point: in the kinematic circle I am talking about, the
circle is also rolling. If you are in an orbit, for instance, the
circle is not moving laterally, but a point on the circle is
moving. The
circle is rolling in place,
and it is moving exactly like the point in the cycloid.
Therefore, we see it is not the lateral motion that adds the 21%,
it is the rolling alone. A static circle and a circle drawn by
motion are not the same. The number π works only on the given
static circle, in which there is no motion, no time, and no
drawing. Any real-world circle drawn in time by a real object
cannot be described with π.
If we study
the generation of the cycloid closely, we find more evidence of
this, since the arc of the cycloid isn't some sort of integration
of the circumference with the distance rolled. It can't be,
because some point on the circle is always contiguous with the
flat surface. We would have to slide
the circle in order to add any
of the x-distance traveled. What is actually happening is that
with the cycloid, the x-to-y integration of distances is
explicitly including time, as you see here:
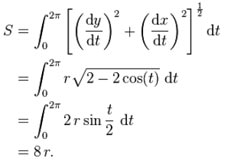
In
that integral, we have three variables or functions: x, y, and t.
Study the second and third lines of the math, where we are
explicitly following the value of t. It is not the sine or cosine
of x or y we are following, it is the cosine and then sine of t.
In that integration, we have three degrees of freedom or a
3-vector. So it is not the lateral motion that is causing the
difference, it is the inclusion of time. To calculate the arc
length of the cycloid, we need the integral which includes dt.
But when we calculate the circumference, we don't include any dt.
So the methods of calculation don't match. Despite that, we use
the naive static circumference that includes π when we calculate
orbits. This is illogical, since all orbits include time. They
should be solved with integrals like the one above, not with the
static circumference calculated from π.
You may wish
to differentiate the two as I
do in my long calculus paper. There I differentiate between
length and distance. A length is a given parameter that does not
include motion or time. It is geometric only. But a distance is a
length traveled in some real time, so it requires motion. A
length is not kinematic, while a distance is. The circumference
2πr is a length. The circumference 8r is a distance.]
In this paper
I will show that if we define π as the relationship between the
diameter and the circumference and
include motion,
the correct value of π is 4.00. In other words, the current
numerical value of π is nothing more than a mathematical error:
it is the standard margin of error, caused by a fabulously false
postulate.
More
specifically, the π that I am correcting is the constant in the
orbital equation v = 2πr/t.
The
Pythagoreans had some inkling of this error. They were never
happy about the irrational number π , just above the number 3.
We have been taught that the Pythagoreans were unhappy about π
due to the fact it was not rational. But their unease was likely
caused by a more fundamental problem. They may have intuited the
problem I am showing you on some level. They seem to have smelled
that something was wrong here. Meaning, perhaps it was not the
value of π that bothered them, much less its status as
rational or irrational. No, they didn’t even spend much time
seeking a precise value for it, since they had no respect for π
to start with, regardless of how you categorized it. Had it been
rational, they would have had no more respect for it. They had no
respect for π because they suspected it was an outcome of bad or
incomplete math. They did not want any rational or
irrational number slightly above 3, no matter what it was,
because they felt the right answer must be 3. What bothered them
most is that they could not complete the math. I will do that
now. Unfortunately, although I will show that their unease was
justified, their intuition was faulty. The correct number is not
3 but 4.
In previous
papers, I showed that classical geometers have sought solutions
by ignoring the time variable completely. The equations of
geometry happen at some imaginary instant. Not only are we at a
limit with regard to length (since all lines have no width,
etc.), we are at a limit with regard to time. We have reached the
limit where t=0, since time is not passing. We don’t take into
consideration how long it takes to draw the lines or curves, we
simply take them as given. We do not imagine traveling along
those lines, or imagine seeing them traveled by a point. The
circle is not an orbit, for instance, it is just a circle,
existing all at once.
But, as I
also pointed out before, geometry cheats in this, since geometry
is supposed to represent the external world, but the external
world never exists in this way. Never once in the history of the
universe has a circle drawn itself or existed all at once.
Currently we assume that π exists in the real world, but I will
show that π exists only in abstract geometry, and that abstract
geometry is kinematically false. That is to say, π does not and
cannot exist in physics or applied mathematics, except as a fudge
factor. We require it so often in our equations only because our
equations are incomplete or misdefined. If our equations
contained all the proper logic and transforms, π would be
extinct.
Let me first
explain what I mean by that in a bit more detail. The number π
is a relationship. We already know that. Currently we think it is
a relationship between the diameter and the circumference. The
problem is, we treat the diameter and the circumference as
equivalent mathematical entities, when they are not. One is a
line and one is a curve. If we study the line and the curve with
a bit more rigor, we discover they aren’t directly comparable.
To state it yet another way: we assume that we can straighten out
a curve like a piece of string, measure it as a straight line,
and then compare that new length to any line we like. Physically,
this turns out to be a false assumption. The only place we can do
that is in abstract geometry, where time does not exist, and
where lines and curves can be “given”, rather than drawn or
created in any physical sense. If we are given lines and curves,
and if we can ignore time, then we get π as the relationship
between the diameter and the circumference. The number π only
exists when we are given absolute pre-existing values, when the
circumference is treated as a simple length, and when we ignore
time. But since with any real circle both these assumptions are
necessarily false, π does not exist in any real circle. In any
real circle, the relationship between the diameter and the
circumference is not π , since the circumference may not
be thought of as a straight-line distance. Because the
circumference cannot be created with a single velocity vector
(and the diameter can), the two numbers cannot be compared
directly.
But let us
start at the beginning. By definition, a velocity vector cannot
curve. A velocity takes place in one dimension or direction only.
In a velocity, there is only one distance in the numerator and
one time in the denominator. These times and distances are also
vectors, and may not curve. But to create a curve, either
mathematically or physically, requires at least two velocities
happening over the same interval. Or, to put it another way, it
requires two distances measured over the same time interval. If
we sum these velocities over the same interval, we achieve an
acceleration, and thereby—assuming the two velocities are at an
angle—a curve.
If we bring
time back into the problem of the circle, we find that every line
or distance becomes a velocity and every curve becomes an
acceleration. So the diameter becomes a velocity and the
circumference becomes an acceleration. All we have to do is
imagine the lines being drawn. The pencil must have some velocity
or acceleration as it moves along the line or curve. Likewise
with a planet drawing out an orbit, or any other possible
creation of a circle in the real world.
Once we do
this, we see that in comparing the diameter to the circumference
in any real circle we are comparing a velocity to an
acceleration. But you cannot directly compare two numbers, when
one is a velocity and one is an acceleration. Or, you can if you
like, but the new number you get from the ratio is not going to
be a number that carries any real meaning in it. It is certainly
not the same as comparing one distance to another. For example,
if you compare one distance to another by putting them into a
fraction and achieving a new number, this new number will contain
useful information. It will tell you how long one line is
compared to the other, obviously. But if you compare a velocity
and an acceleration, what information do you get? Say you achieve
the number 5, which tells you the acceleration is five times the
velocity. Does that tell you anything about distances? Yes, it
might, if you develop a transform. But without a transform and a
bit of thinking, the number 5 isn’t telling you anything. It
certainly isn’t telling you that some distance is 5 times some
other distance.
To give a
specific example, what if my acceleration is 3 and your velocity
is 1. Can we compare those two numbers directly? No, we cannot
put them into a fraction or any other equation without doing some
more work upon them. We cannot claim that I have done anything
three times as much as you. With an acceleration of 3, my
velocity could be anything at a given interval, and my distance
traveled likewise. What if my acceleration is π and your
velocity is 1? Is π the value of any real relationship between
us? No. You can’t compare an acceleration to a velocity. You
need more information.
To say it
another way, think of the calculus. In the calculus, velocities
and accelerations can't be put into the same equation—without
the proper notation. Velocity is the first derivative and
acceleration the second, so we have to notate a velocity variable
or function with a single quotation mark, and an acceleration
with a double (or something similar). If we don't, the equations
will soon implode. The functions indicate different rates of
change, so they can't be compared directly. The functions have to
be kept separate and handled in the right way, and everyone knows
that. But in the historical orbital equations, they haven't been
kept separate. Whenever we compare the circumference to the
diameter directly, finding π, we are breaking this fundamental
rule of the calculus.
This is
important because this is precisely what we think π is telling
us. We think it is telling us that the circumference is
3.14 times the diameter. But it isn’t. About real kinematic
circles, π is telling us nothing. About abstract circles, π is
telling us that if the circumference were a straight line,
it would be π times the diameter. But since the circumference is
not a straight line, π is telling us nothing useful there
either.
To show this
more clearly, let me give you another example, with a diagram.
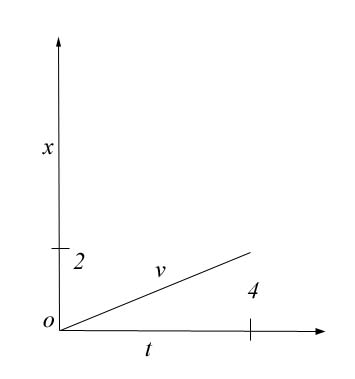
Here we have
a Cartesian graph of a velocity, with axes labeled x and t. As we
know, a velocity on such a graph is a straight line. The line
stands for or represents the velocity. But what does the length
of that line represent? In this example, x = 2 and t = 4, so v =
x/t = .5. But the length of line v is much longer than .5 units.
The length of line v can only be found by the Pythagorean
Theorem, and it turns out to be about 4.47. Now, we can ask what
is the ratio of line v to line x, and we will find it is about
4.47/2 = 2.236, which is an irrational number. An esoteric ratio?
Of course not, since the length of v is not only a meaningless
length here physically, it is not even the real velocity. By the
definition of velocity, the velocity is the distance over the
time, so using the Pythagorean Theorem to find the length of v is
just foolish. I claim that, in a physical situation, comparing
the length of the circumference of a given circle to the length
of its diameter is just as foolish.
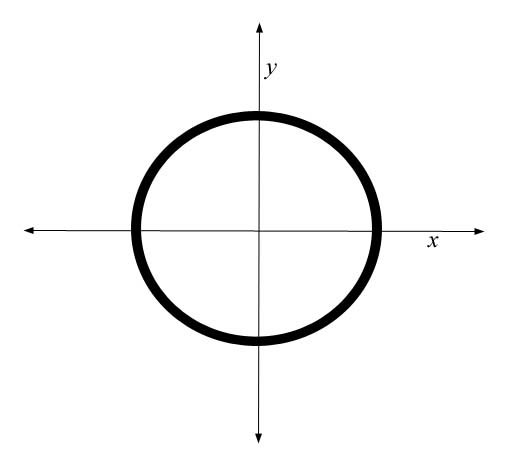
We can draw a
circle on a Cartesian graph, too. We can’t make one of our axes
a time axis, but we know we can draw a circle on an x/y graph,
since a well-known equation comes with it (x2 + y2
= r2). Here we are taught that the circle represents
an acceleration, as all curves are accelerations on Cartesian
graphs. But what about the length of the circumference of this
circle: what does it represent? Just as with the line
representing the velocity in the first illustration, it
represents nothing here. You wouldn’t think of comparing that
“length” to the radius or the diameter in this illustration,
so why would you do it when you take away the graph?
Of course,
this analysis begs the question: what “graph” is a real
circle drawn on in the real world? When a planet “draws” an
orbit around a star, what mathematical background are we using?
Put that way, this problem starts to look very complex. We have
three dimensions, x, y, and t, and a complex motion. The orbit is
not just a velocity or an acceleration, it is a
simultaneous velocity and an acceleration. To draw out the
circle, the planet has to be expressing both a tangential
velocity and a centripetal acceleration over every dt. We are
told that the planet will have an “orbital velocity”, but
that wording is criminally reductive and misleading. Not only
does the planet NOT have an orbital velocity, it does not
precisely have an orbital acceleration either. It does have a
sort of acceleration, but that acceleration is not like any
first-degree acceleration we are accustomed to measuring. No, it
is a very odd beast altogether. It must be called an acceleration
for two reasons: 1) It curves. A velocity is a vector and cannot
curve. 2) It requires a constant force. A velocity is achieved
with a single force. An acceleration requires a continuous force.
A circle requires both a single force and a continuous force,
therefore it must be the expression of some sort of acceleration.
But it is a unique compound acceleration, compounded of both an
acceleration and a velocity.
And that begs
another question: is 2πr/t a velocity? No, since a velocity
cannot curve. Is it an acceleration? No, since you can’t
achieve an acceleration by dividing a distance by a time. What is
it? It is a floating heuristic device, a piece of fake math that
misdirects us. It causes us to think of the orbit as an abstract
geometric shape, where time can be stirred back in in a sloppy
manner at the end. But neither the orbit nor the circle should be
thought of that way. As I will show in more detail below, 2πr/t
is actually a variable or second-degree acceleration, of the form
x/t3. This is because π is already an acceleration
itself. This gives 2πr/t the dimensions of x/t2/t,
which reduces to x/t3. This is logical, since we need
the three t variables in order to express the simultaneous
tangential velocity and centripetal acceleration that makes up
the orbit. The velocity contributes one t variable and the
acceleration contributes the other two. The orbit is neither a
velocity nor a simple acceleration. It is a second-degree
acceleration.*
Now,
hopefully, you begin to see the problem. Historically, we have
been seeking a relationship between distances, and historically
we have thought that π has been an expression of that
relationship. But it isn’t. The number π is an expression of
the relationship between two lengths that exist only in abstract
geometry, and abstract geometry is physically false. In the real
world, if we want to know the relationship between the diameter
and the circumference, we have to look at the relationship
between a velocity and a second-degree acceleration.
You will say,
“But surely that acceleration will give us a distance, as will
the velocity. Are you saying that the distance given by that
acceleration is not 2πr?” Yes, that is precisely what I am
saying. If you use straight-line motion to measure everything
(which is what we do physically), then a curved string must be
longer than a straight string. And the very simple reason for
that is that it must take longer for any real body to travel
along the curve than along the straight line.
One key term
in that last paragraph is this one: “straight-line motion.”
Notice that I do not say, “the straight line.” In reality, we
do not use a straight line to measure, we use straight-line
motion. We use a velocity vector to measure the real world. This
can be seen very clearly in my explanation above: The real world
includes time. In physics, you simply never have a distance
divorced from time, like you have in geometry. Every distance
comes with a time, and cannot be separated from it. When we
insert time back into the circle equations, all the lengths
become velocities. The diameter is not a length, it is a
velocity. Now, if we compare the diameter to the circumference,
what we are really doing is measuring the circumference
with the diameter. So, if we are measuring with a velocity, and
it takes longer to travel a curve than a straight line, the curve
must be longer. This must be true even when the curve and the
straight line have the same length in abstract geometry.
Another key
term in the paragraph before the last one is this one: “it must
take longer.” When measuring a curve with a straight line or an
acceleration with a velocity, we are not measuring with x so much
as we are measuring with t. Look at it this way: if you have a
constant velocity, then the distance traveled is simply a
function of time. If you travel two lengths, the one that took
longer will be longer. Since a curve is not equivalent to a
straight line, we should measure them with time instead of
length. We can tell how long the curve is by seeing how long it
takes us to travel it.
Finally,
remember that the distance traveled by an acceleration is never
just the velocity times the time. So neither an orbital velocity
nor an orbital acceleration could be expressed by the term 2πr/t.
If you are given a normal acceleration and seek the distance
traveled in some time, you must use the equation x = at2/2.
But we don’t have a normal acceleration; we have a variable
acceleration, one that is not linear, and we seek the distance
traveled in some time. What equation do we use? We are in new
territory here, since there is no standing equation to plug into.
We must create it from whole cloth.
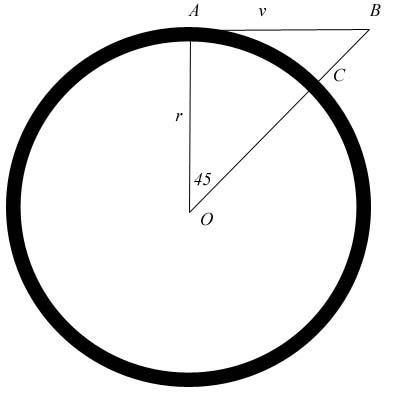
To arrive at
that equation, let us first look at some other thought problems.
These thought problems, with their accompanying illustrations,
may give us a clue how to proceed. As our first thought problem,
let us say you are in a spacecraft traveling at velocity v. You
are approaching a planet. You happen to know its gravity
precisely, so you arrange to intersect its field at precisely the
right angle and distance, so that your velocity creates a stable
orbit. In real life, this maneuver would require some
adjustments, but we will assume you can slip right in there. To
make this even more interesting, let us say that your orbit has a
radius of fifty miles and you are going fifty miles per hour. The
planet is very small and happens to have a gravity vector that
makes this stable. Both logic and Newtonian mechanics tell you
that it will take you eight hours to orbit (see the illustration
below). Let us imagine further that you are an alien from some
planet that knows nothing of π and that does physics a bit
differently, and you calculate the orbital distance like this:
your velocity was the same both before and after entering orbit;
your engines are in the same state as they were before, both as
regards direction and strength; you haven’t throttled up or
down or moved a tail fin. Since distance is velocity times time,
you calculate the orbital distance to be 400 miles.
Are you
wrong?
According to
abstract geometry and π, of course you are. The circumference of
the orbit is about 314 miles, not 400. Your orbital velocity is
about 39 mph, not 50. And what is slowing you down is gravity,
which tends to pull you back slightly, working against your
engines.
But there are
a lot of problems here. If we use general relativity, our
mechanics is immediately out the window, since there is no
centripetal force. The curvature pre-exists in the orbit: it is
not caused by a pull, so only your velocity exists. If your
velocity is the only motion that exists, and if a straight line
is equivalent to a curve, there is absolutely no reason you
should not calculate the orbital distance to be 400 miles. There
is nothing pulling you back or working against you engines, so if
you aren’t being slowed down, you must be going the same speed.
If you are going the same speed for the same time, you must go
the same distance. If you aren’t being slowed down, then your
“orbital velocity” cannot be less than your original
velocity.
But it is
even worse than that, from a physical viewpoint. Let us ask if it
is possible to apply a centripetal force without affecting a
tangential velocity. Let us assume there is some force
turning the spaceship, either Newton’s gravity or some real
force that is “warping” space. The problem with this is: the
spaceship’s engines are off! When glossing the standard model
response, I said that gravity was working against the spaceship’s
engines, slowing it down. But a constant velocity requires no
engines in space. Does the Moon have engines? No, all we require
is an initial force, to get the Moon or spaceship going.
After that it coasts at a constant velocity (this is all
according to the standard model and the historical
interpretation).
To make this
problem even clearer, let us say we want to create the appearance
of an orbit using just the power of the spaceship. Meaning, we
want to draw a circle in space without a central body.
Theoretically, we should be able to do this with just two
engines: one to get us started in the forward direction, and one
to push us constantly toward some chosen center. This second
engine will run all the time with a constant thrust, and its
direction will change every moment. I hope you can see the
problem. Even if we could build a directional thrust to the
engine that could change smoothly and accurately, we could not
keep this thrust from interfering with the original velocity. You
can neither push nor pull on a real object at a true
perpendicular to the line of motion of that object, since a real
push or pull is never instantaneous. Our push here, like gravity,
must be continuous, which must create some real time interval,
which must create some non-tangential component, which must
interfere with the initial velocity of the spacecraft. Any real
pulling or pushing force, even one at a tangent, must tend to
dissipate an initial velocity.
Circle
mechanics makes this even clearer, since the force of gravity is
not strictly perpendicular anyway. To create the circle or the
orbit given an initial straight line velocity requires some
backward component to the central force. You can see this
immediately just by comparing the tangential velocity and the
“orbital velocity”. As I showed above, and as every engineer
knows, the orbital velocity is less than the tangential
velocity. This alone proves that there is a component of force
backward along the line of the tangent, for if there weren’t,
the tangential velocity would have to be equal to the orbital
velocity. In other words, gravity must pull down and back.
If it just pulled down, no circle or orbit would be created.
Because the spaceship is moving forward, gravity must pull
down and back. Look at the illustration below. BC is the gravity
vector. To go to the limit, we make the triangle ABC as small as
we can. We cannot make it zero, since AB must have some length.
If AB has no length, then the spaceship has zero velocity. If the
spaceship is moving, then AB has some length. If AB has some
length, then BC must have some backward component. If BC has some
backward component, it must tend to diminish the velocity AB.
QED, gravity must tend to diminish the tangential velocity of the
spacecraft or the “innate motion” of the Moon.
The standard
model response here is that I am wrong: the centripetal force
must be completely perpendicular to the initial velocity at all
times, therefore there is and can be no “backward” component
to the force or the acceleration. I will be told that this is why
the Moon’s innate motion does not dissipate. But if this is
true, then why is the orbital distance less than the distance
that would have been traveled at the original velocity? As the
illustration shows clearly, a tangential velocity of r would
create a distance traveled of 4d, not πd. If the centripetal
force does not work against the tangential velocity, as a
vector, then how can πd be less than 4d? To put it another way:
if the centripetal force is completely perpendicular to the
tangential velocity—even while we sum the times involved in a
complete orbit—then the tangential velocity must be unchanged.
If the tangential velocity is unchanged over each dt and the sum
of all dts, then how is it that the orbital distance is not the
same as the expected straight-line distance? And how is it
possible that the orbital velocity is less than the tangential
velocity?
I say that in
order for the compound or “orbital” velocity to be less than
the original or tangential velocity, the centripetal force must
be working against it, in a vector sense. This is the only
possible way the orbital distance (the circumference) could be
less than 4d. But if the centripetal force is diminishing the
total distance traveled, it must be diminishing the tangential
velocity. And if it is diminishing the tangential velocity, that
velocity must be dissipating, and the innate motion of the
orbiter must be dissipating as well.
In fact, if
we accept the standard-model interpretation, the orbit would be a
sort of perpetual motion machine. Without perturbations and other
orbital imperfections, a planetary orbit would be perfectly
stable, according to both Newton and the current standard model.
It would not tend to change either inward or outward. The
standard model allows for such a possibility in the real world,
since neither the tangential velocity nor the centripetal
acceleration is a cause of orbital instability. Theoretically, a
perfectly round planet in a perfectly round orbit around a
perfectly round star, at a distance from all other planets and
stars, might orbit forever. And since in General Relativity,
curvature is given rather than created, this motion conserves
energy. Since it both conserves energy and creates potential
energy, it must be a perpetual motion machine. Remember, we have
a non-dissipating curve here! That is not only perpetual motion,
that is a perpetual machine: a perpetual source of power.
Now, I have
not put the analysis in these terms in order to sell a perpetual
motion machine. I have put the analysis in these terms to show
that the standard model is contradictory and flawed. I need to
get back to π, so I will tell you the end of this story and move
on. The short answer to this problem is that circles and orbits
aren’t created this way physically or mechanically. We can
analyze the circle mathematically in this way if we do it right
(which historically we haven’t), but in the real world circles
and orbits are never created with simple tangential velocities or
“innate motions”. A protractor does not draw a circle using a
tangential velocity, a boy whirling a ball on a string does not
use a tangential velocity, and no other circle is ever created in
this way. The protractor and the boy and the tilt-a-whirl and so
on make use of constant tangential forces, not just centripetal
forces, and they would have to do so even if friction were not a
factor. Regarding celestial orbits, the mechanics fails there,
too. Velocities would dissipate, planets are not self-propelled,
and the balance could not be maintained. As I show in
a series of other papers, celestial orbits are more complex
than we have been taught. They include the E/M field, for a
start, which acts as both a balance and an engine. And we have to
reverse the gravity vector, which makes it neither a push nor a
pull. It is a real acceleration of the central body, so it causes
no forces and no dissipation in the Newtonian sense.
That being
said, we can still analyze the orbit and the circle in much the
way Newton taught. We can use his equations, we just have to
clean them up a bit. To do this, lets us look again at the last
illustration. This drawing requires a more rigorous analysis,
both as it applies to orbits and as it applies to circles created
in any other ways. If you have studied this problem at all, you
have probably seen hundreds of drawings, with polygons inscribed
and superscribed on circles and so on and on. But all those
drawings are misdirection. The important drawing is this one.

Here we
measure the circle with the radius directly. We treat the radius
as a velocity instead of a distance, and then begin our trip from
some point on the circle. I am starting at point A in this
drawing. In the drawing, the length of the vector stands for the
velocity, and I must draw it at a tangent. Meaning, the angle at
A must be 90 degrees. So, if you give me the same time to travel
as I took to draw the radius, then I will end up at point B.
But if we
want to draw a curve, we must keep the pencil on the circle, and
here I am way off the circle. How do we solve this? Let us solve
the way Newton did, by inserting a second motion. To create any
real curve requires at least two simultaneous motions. As we know
from classical orbital mechanics, this second motion must be a
vector pointing at the center. This motion will take us from off
the circle to back on the circle. To get us back on the circle,
we can postulate a constant force over the interval of motion,
and this would give us an acceleration, just as in gravitational
mechanics. Or, to avoid that variation, which mathematically
would require the use of calculus, we can just postulate all our
force at the end. In that case, the final velocity is the
acceleration, since we have a change from zero. The acceleration
can be found just by drawing a line from B to O. The length of
the line BC then represents the centripetal acceleration of our
pencil over the interval AC. Those two motions or velocities
happen over the same interval, so the two times superimpose.
Whatever time it took us to draw the radius initially, is the
same time it now took us to go from A to C. Therefore we have
measured the circumference using the radius.
But how does
this give us a circumference? Before I show you the full math,
let me show you the conceptual shortcut. Go back to the drawing
above. You can immediately see that we have carved out a piece of
pie that is 1/8 of the circle. AO = AB, so the angle at O is 45
degrees. Eight pieces of pie means we use eight radii to measure
the whole circle. That is 4 diameters. Problem solved. It takes
us four times as long to travel the circumference as to travel
the diameter, given the same velocity. If the velocities are
equal, and the times are directly comparable, then the distances
are directly comparable. Velocity is d/t, so if it takes us four
times as long, the distance must be four times as much also. That
is the only real way to compare a velocity and an acceleration,
or a straight line and a curve. Every other analysis is
incomplete and faulty, since every other analysis ignores the
time variable.
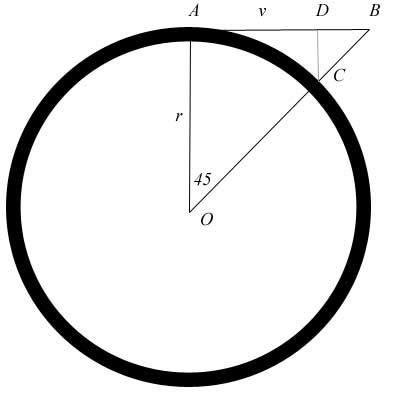
Now let us do
the full math. Let us go back to the illustration, to start. Let
us drop a perpendicular from point D so that it hits point C, as
above. Since the angle at B is 45o, DB must equal DC.
And now I will prove very quickly that AD + DC is equal to the
curve AC, in length. As I do that, I will have also proved that
AB is equal to the curve AC, in length, which will prove my
assertions above concerning the falsity of π . If I can prove
that, it will prove that the circumference is 8AB, not 2πAB.
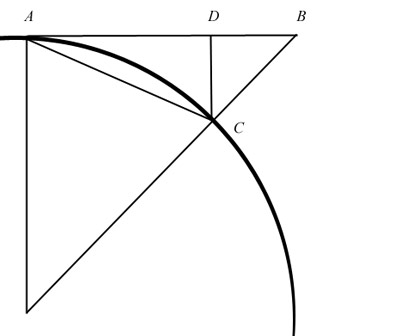
The
historical way of finding the length of arc AC is by exhaustion
or by calculus. We look at smaller and smaller subarcs until we
reach the limit where the arc equals the chord. The chord is
simply the straight line from point to point: for example, the
straight line from A to C is the chord AC. If we can straighten
out the arc, we will have measured it, and we can use that length
to compare to other straight lines. So we let C approach A. At
the limit, it is assumed that the chord AC is the length
traveled. The Greeks used this analysis and these assumptions in
solving this problem over 2000 years ago, using the idea of
exhaustion (which I will return to in a moment). Later, when the
calculus was formalized, we went to an ultimate ratio, as Newton
called it; and then we went to a limit, with Cauchy. But in all
the historical solutions, the assumptions were as I have stated
them in this paragraph. The main assumption being that we were
taking the arc to the chord: approaching the chord in some way or
fashion.
But all this
is false. The very simple fact is that the distance traveled
never approaches the chord. The distance does not approach
anything, since it never diminishes. The distance is the same
whether we draw it large or draw it small. Since it doesn’t
change as we “exhaust” it, it cannot approach a limit. Watch
closely as I prove this in my diagrams, with simple logic.
In my
analysis above, I showed that the centripetal force must pull
down and back in order to take any object—either a
pencil tip or an orbiting spacecraft—out of its original path
and into a circular path. The simplest way to think of this is to
think of the original velocity as AB. Then the centripetal force
creates two other velocities: a velocity of size DB, which pulls
the body back from B to D; and a velocity DC, which pulls the
body down to its final destination of C. This is how we break
down our curve into straight velocity vectors. The motion of the
body from A to C is a summation of these three vectors. All three
velocities happen over the same time interval, so we sum them. It
is that simple.
You will say,
“That makes some sense, until we look at the actual lines. Any
idiot can tell that AD + DC must be longer than the curve AC. The
curve AC never goes out to point D, for a start. If you want to
solve by exhaustion, you have to “push” the point D closer
and closer to the curve, by dividing that curve into lots of
little segments or steps. That is how the Greeks actually solved
it, you foolish person. You can’t just take any large arc like
this and run perpendiculars: you have to go to a limit. You have
to get small.”
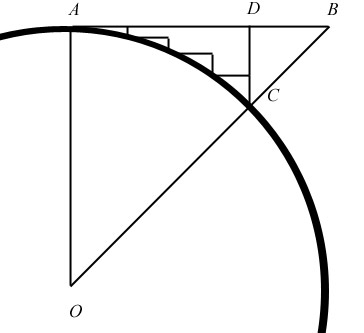
OK, well, let
us do that, then. In this diagram, I will push D closer to the
curve AC. I will begin both the exhaustion and the “approach”
to an infinitesimal or limit. We will start by dividing the curve
into 4 equal parts or steps. And yes, we are much closer to the
curve already, as you see, with just 4 divisions. We don’t find
ourselves anywhere near the distance from the curve of the
original point D. It already appears that if we continue to do
this, we will “approach” the curve AC very fast, so our
method appears to be the right one. It does what we want it to,
and it mirrors the method of the Greeks and Moderns.
The problem
is, it doesn’t change the distance traveled at all. If
you add up those eight little lines segments along the steps, you
find that they equal AD + DC. We have changed our path, but we
have not changed our distance! We can draw eight steps or 64
steps or an infinity of steps, and it will not change a thing.
With our logical little method here, we are not “approaching”
any new distance, we are only approaching a new path. The
distance is the same at the limit as it was in the beginning: AD
+ DC.
Therefore, at
the limit, the path AD + DC is equal to the path taken by
the curve AC, which does indeed solve our problem. But the
distance has not changed by going to this limit. So if AB
is the same length as the radius, and we have defined the radius
as .5, then AC must .5 also, and the circumference is 4.
It turns out
the aliens were correct again. I said above that they had no idea
of π, and that they simply used their tangential or original
velocity to measure the circumference of the orbit. I have just
shown why they are correct and why we are and always have been
wrong.
There
is one more thing to notice here before we move on. It is very
important. I have shown that AD + DC = arcAC. In my diagram, this
means that the tangent equals the arc. However, this works only
when the tangent is equal to the radius. The angle at O must be
45o,
so that DC = DB. If the angle is not 45, then the tangent cannot
equal the arc, because AD + DC is not equal to AB.
This
is important because if we assign the tangent to the tangential
velocity and the arc to the orbital velocity, as Newton did, we
find they are equal not at the limit, but only when the tangent
equals the radius. In fact, as
I have shown, the tangent and the arc are NOT equal at the
limit. At the limit, the tangent remains longer than the arc. And
this means that the tangential velocity and orbital velocity are
equal only when the length of the tangent is equal to the radius,
or when the time is equal to 1/8th of the orbital period. An
orbital velocity found by any other method will get the wrong
answer. This
is why 2πr/t is wrong: 2πr/8 is not equal to r.
Ditching
π allows us to further correct the orbital equation. I have
already shown that the equation should be a = v2/2r
instead of v2/r.
If t is the time of one orbit, then the orbital velocity must be
8r/t, not 2πr/t. These two corrections change the value of a
from 39.5r/t2
to 32r/t2.
In a supplement to this paper, I will show how this solves the
famous Explorer
Anomaly.
After
we have made all these corrections, we are in a position to see
that we may assign the acceleration a to the line segment BC.
Furthermore, if a = v2/2r,
and AB = r, then r = v, and a = r/2. Consulting the diagram above
again, that is also 2BC = CO. What this means is that we have a
new way to find a centripetal acceleration, currently called
gravity. The equation a = r/2 gives us a total acceleration over
1/8th of the orbit, so the total acceleration over the entire
orbit is 4r. Or, we can find the acceleration over any
subinterval. Say we want to find the acceleration of the Moon
over 1 second. We are given that the period for the Moon is
2,360,534s. Since the Moon is orbiting at 384,400,000m, the total
acceleration over the orbit is 4 times that, or 1.538 x 109.
Dividing gives us a = .000276m/s2
over 1 second.
For
more fun, we can even show that the centripetal acceleration is
not found at an instant. I
have shown that the Moon's centripetal acceleration due to
the Earth is not .002725, it is .002208. If the Moon's total
acceleration over 1 second is .000276, then an acceleration of
.002208 cannot happen over an instant. We can even find the time,
with simple math. If we plug that into our new equations, we find
that a = .002208 when t = 8s. That is not an instant or an
infinitesimal, since it is a calculable number. That would be
true even if I used the number .002725 for the Moon's
acceleration. You cannot have a real acceleration over an
instant, so we should have known simply from logic that the
centripetal acceleration we have been calculating was not over an
instant or infinitesimal. I have just calculated the real time of
orbit during the "instantaneous" acceleration, so I
have proved that Newton did not go to a limit or approach zero.
As I have said in my
paper on the derivative, the calculus does not work by going
to zero or a limit, it works by going to a subinterval, and I
have just shown you the subinterval in a specific problem.
Some
will say this is just doing the calculus wrong, but I claim that
history has done the calculus wrong, not me. The common answer to
my demonstration above is that at the limit, defined as it
currently is, the total length of the steps never approaches the
arc, because even with a very large number of steps, the distance
between each step and the curve remains real. We can sum this
distance even at the limit, keeping the sum of the steps above
the sum of the curve. It is not the sum of the steps that
approaches the curve, it is the curve that approaches the chord.
In other words, it is the hypotenuses of the little triangles
that converges upon the curve, not the sums of the other legs of
the triangles.
While
I recognize that this is the common interpretation, I cannot
agree with it. In my paper on Newton's
lemmae, I proved that the tangent in his triangle must be
longer than the chord and arc at the limit. If we apply that to
this problem, it means that the arc cannot approach the chord at
the limit. The tangent is a component of the arc, by Newton's own
definition of it in the Principia,
so if the tangent is longer than the chord at the limit, the arc
must be also. This means that the curve does not approach the
hypotenuses of these steps, no matter how many there are. The
hypotenuses are the chords, and they cannot be approached by the
arc or tangent.
You
will now ask where in the Principia
Newton says that the arc is
composed of the tangent. It is where he tells us that the orbital
motion is composed of the centripetal acceleration and the innate
motion of the body. These two vectors compose the orbital motion.
They are the only two motions given us by Newton, and he
explicitly assigns the innate motion of the body to the tangent.
This
means that the historical and current interpretation cannot be
correct. The hypotenuses do not converge to the curve or the arc.
No, as I show above, it is the tangent that converges upon the
arc, but the convergence happens only when the tangent equals the
radius. This convergence can happen only at 1/8th of the circle,
and it happens just as I show in these papers. It happens because
the arc is never a continuous curve, even at the limit. The arc
is defined as a curve composed of linear or straight vectors,
therefore it can never be continuous, if we mean by continuous
that the time or length traveled goes to zero. Logically, the
time or length cannot go to zero, since there is no time or
length at zero. All numbers in math and physics imply a
differential, and since this is so, the curve cannot be thought
of as continuous in this way. The curve must be thought of as
composed of linear vectors, even at the limit. And since this
must be true, it must also be true that the path I have drawn
above must converge upon the arc, for precisely the reasons I
have stated. The path does converge upon the arc, in the sense
that the path gets nearer the arc. No one can deny that, at
least. But since the arc is not continuous even at the limit, the
path truly does converge upon the arc, as we draw more steps.
Since the distance doesn't change no matter how many steps we
draw, the tangent must converge upon the arc. Or, at 1/8 of the
circle, the tangent simply IS the arc.
Let me round
out this “full math” by answering a couple of questions. I
have shown the simplest full math, and it may not convince some
people. I will be told, “It appears that your method of
‘exhaustion’ can be used to show that any curve from A to C
is of the same length. Beyond that, it would appear that even the
chord AC can be shown to be equal to AD + DC, by your method.
What makes the circle arc AC special, and why should your method
work upon it and upon no other arc or line between A and C?”
It is a good
question, admittedly, or I would not include it here. To make
this method—which I have called exhaustion but which might just
as easily be called approaching a limit—work, we have to push D
toward the curve in a rigorous manner. In short, all of our steps
have to be approaching the curve at the same rate, or the method
will not work. For instance, if we draw a different curve from A
to C, one that bulges out very near to D, and then we draw our
steps, we will not be able to make those steps even. Or, to put
it another way, we will not be able to push D toward the curve in
an even manner. Our exhaustion will not “go to infinity” at
the same rate all long the curve; therefore our method will not
work, mathematically or physically. But it will work with the
circle arc AC, and it works for the physical reason I have shown
above: both the tangential velocity and the centripetal force are
constant. The arc AC is created by a constant and unvarying
process, therefore that arc can be approached by the (right)
orthogonal vectors in a logical and rigorous manner. In fact, the
arc AC is the only curve from A to C that can be exhausted in
this manner, given AD and DC. All other curves are varying
curves, and cannot be approached as a limit or exhausted in this
direct way.
To show why
the chord AC cannot be approached like this, we use much the same
analysis. At first look, it appears that you could draw steps
along the chord AC in the same way, “exhaust” them in the
same way by increasing the number of steps higher and higher, and
find by this magic that the straight line AC was the same length
as AD + DC. The reason you cannot do this is because once again
you cannot approach the chord AC in an even manner from the point
D. Therefore all your steps won’t go to the limit at the same
rate, and your “method” won’t work. You will say, “Gosh,
it seems like the straight line would be the easiest thing to
approach in an even manner, since it is even to start with!”
But try it and you will soon see this is not the case. The
straight line is actually the most difficult thing to approach,
and the impossibility of this approach is actually the easiest to
discover. For instance, draw four equal steps along AC, then look
at them from the point D. There isn’t any way you could have
approached those four equal steps from D. In the method, you
aren’t just drawing any steps you like. You are supposed to be
drawing steps that would occur if you pushed the line AD + DC
toward AC. Exhausting a process or going to a limit is not a
willy-nilly process, it is a defined and rigorous process. You
will find, if you try, that you can’t approach a line evenly
from any point, using this method. No matter where you
place D along the line AB, it will not approach AC at the same
rate, with steps logically defined in any possible way. And it
may eventually become clear to you why this is so: the distance
of a line cannot be approached from off the line, because the
line is already the distance itself. It is “even to start
with”; therefore, it cannot be approached evenly (except by a
parallel line of the same length).
As one more
short demonstration of this, say we place D on the line AB so
that it is equidistant from A and C to begin with. You may think
we could make it approach AC in an even manner in this way. But
no. If we draw smaller steps in the middle and larger ones toward
A and C, we can force one set of steps to act right. But we
cannot make our next set of steps act right, both in regards to D
and in regards to our first set. To make our next set of steps
diminish evenly, we would have to vary the rate of change along
the steps, and this isn’t allowed. An approach to a limit must
progress in a defined way, else the approach won't happen. An
approach that progressed unevenly would create "bumps"
as the limit was approached, and the limit would not be the curve
we see. It is one thing to approach a limit that is a point, and
another to approach a limit that is a line or curve. In
approaching a line or curve, the approach has to be the same at
all places along the curve, and to achieve this the approach must
be monitored all along the curve, as I am showing you.
There are
more abstract ways of stating this, in various mathematical
symbolisms, but because math is always shorthand for the
explanation, I prefer to give the explanation. If you don’t
comprehend the explanation, you won’t ever comprehend the math.
To ever understand the curve or calculus, you have to study
diagrams and do some real pushing and pulling of lines, just like
this. A limit is not an abstract thing. It is not a concept you
can use like a hammer, without finesse. You have to understand
that a limit is always approached in a rigorous and defined
manner; and if it is not approached in a rigorous manner, you
will get the wrong answer. The same thing applies to exhaustion.
Mathematically, exhaustion is a rigorous process. It is not just
drawing more and more steps; it is drawing steps that increase in
number and size in a defined manner.
The very
shortest answer to this question is that you can approach the
circle arc AC from the line AD + DC because those vectors created
the arc AC to begin with. Those vectors physically created the
curved path. They are not just orthogonal vectors, chosen because
they were handy. They are THE orthogonal vectors that define the
path of the curve. The arc AC is approached smoothly from D
because it was in some sense created from D. D is the physical
balance of O, given the interval AC and motion from A to C. D was
guaranteed to approach the arc AC smoothly and evenly, which is
why I use the method without explanation in my gloss of this
paper.
Now, some may
ask what this has to do with my whole analysis of time, earlier
in this paper. I spent many pages telling you that time changed
the whole problem of the circumference and its measurement and
then I offered a "full math" that didn't once mention
time. Here we get into some difficulty I wanted to avoid. I have
been trying to avoid bringing calculus into the problem here,
since I have already been forced to redefine the calculus in
another paper. Bringing all that into this paper was
something I hoped to skirt, retaining a transparent explanation
to the end. For some readers I will have achieved that already.
For others (the ones asking about time now) I won't. For these I
will attempt a transparent explanation that still avoids a full
use of the calculus, either the historical treatment, or my own.
When I say that we must monitor the rate at which D approaches
AC, that rate is time. Whenever someone says "rate" you
should hear "time". In any physical situation, time is
always underneath all our distance measurements. We can draw a
circle and refuse to monitor the time involved in drawing it, but
time is there regardless. It is there when we remember that all
distances are velocities or accelerations; and it is also there
when we remember that limits must be approached in some real and
rigorous way. The curve AC cannot be straightened out like a
piece of string because that curve is a curve made up of both
distance and time. If you straighten it out and measure it like
string, you are measuring the distance but not the time, and so
you get the wrong answer.
There are two
ways to think of this. One is to think of time as an actual
length itself. Say you have a curve and a line that are equal
lengths, according abstract geometry or the string method. The
curve will have more time "embedded" in it. It would
take you more time to travel it at the same velocity (as the
standard model already admits with its "orbital velocity").
Therefore, when you straighten it out, you should monitor both
the distance and the time. If you do this, the time will add to
the distance, and your curve will be appreciably longer than you
expect. You can actually add the difference in time to the end of
the line and get the correct answer, so thinking of time as
embedded in the curve is not just a pretty visualization. It is
mathematically true.
Another way
to think of it is to think of the line and curve as made up of
atoms. Let the atoms be the distance and the separation between
atoms be the time. If you straighten out a curve, you must
compress the atoms, losing somewhat of the separation. If you
have lost this separation, then you have lost part of the "time"
and therefore the distance. A curve cannot be straightened out
without affecting its real length. This is not just a
visualization either. It is physically true. The best way to see
it is again with a diagram:
We want to
straighten the piece of curved string 1-4-5 out into the piece of
straight string 1-2-3. Although it is clear that the curve is
longer than the straight line, let us follow the standard model
and define both strings as equal length and see what happens. I
use this diagram because some will say that no real compression
is involved if we imagine a string with no width. They will say
that a real piece of string will be compressed only on the
outside, as you straighten it, but that the inside of the curve
will be stretched. They will say that a one-dimensional string
will not be compressed as you straighten it. This diagram shows
that is false. Even a piece of string composed of only one line
of atoms, with the distance between adjacent atoms always only
2r, will be compressed. To see this, all we have to do is roll
ball 5 up to ball 3. If we do that, the mark that is the curve
must leak out the ends, showing that compression took place. This
is obviously because the line AB is equal to CDE, not to the
curve. The curve is longer than CDE, and must be compressed to
equal AB.
Those who are
especially prickly will say, "Well, if the curve is longer
than AB, then the two strings were not the same length. You
should define the curve as equal to AB." But if we do that,
we have the opposite problem, in that we can't make the balls the
same size in the curved string as in the straight one. If we
define the curve as equal to AB, then we have to make our balls
bigger along the curve. So that when we roll ball 5 up to meet
ball 3, we again get compression. No matter how you look at it,
you cannot straighten out a curve without materially, and
therefore mathematically, affecting it.
Some will say
that this analysis assumes non-continuity, but it doesn't. It
doesn't even require a quantum view of matter. Those balls don't
have to stand for atoms. They can stand for little number 1's if
we like. They can stand for anything at all, physical or
mathematical, real or abstract, except zero or its equivalent. No
matter what the balls represent, compression is the logical
result.
But let us
return to time. Time is central to this last visualization as
well. A second variable always supplies us with the rate of
change, and thereby the curve, and in the real world, time is
always present: it determines this rate of change, no matter what
other variables are present. Time is the reason that the curve
does not equal AB in this example. The difference between the two
is the difference in time. And the difference is large. The
difference between π and 4 is not small. Historically, we have
mis-measured the length of a curve by a large margin.
Professional
mathematicians will not be happy with all this for several
reasons. One, they will not like to see π treated with so little
respect. Something with such a long history should not be looked
at this closely. It is like looking at your grandmother with a
magnifying glass: impolite and impolitic, if nothing else. Only a
monomaniac would even entertain the idea that all of history was
wrong, about any idea at all. Two, They will not like all this
talk. If I have some new math to relate, I should just plop down
the equations and see if they can remain standing under fire.
This is the expected route to take. Three, they will not like my
"misuse" of the calculus, even if I never claim to be
orthodox. I will appear to them to be taking things to limits in
very strange ways, and explaining myself in even stranger ways.
Given Newton and Cauchy and the rest, I will simply be seen to be
doing calculus wrong. In response, I point out that the
invention of the calculus historically went hand in hand with
analyzing curves, and it was invented to analyze geometric
curves, not kinematic curves. What I mean by that is that
calculus and trigonometry and the orthodox use of limits was used
in an analysis that ignored time. Newton assumed that a circular
orbit could be thought of just like a circle given in geometry,
with no monitoring of time or velocity. In this he was actually
even more reductive than the Greeks themselves, who at least
asked if the point on the curve had a velocity. Some of their
analyses toyed with this idea. But Newton never questioned that
the distance around the circle was a raw distance, like the
geometric circumference. This is why he wrongly called the
orbital velocity a velocity, and this is why we still do it. We
don't include time in the curve, we just try to add it back in at
the end. This is why we retain the ridiculous habit of writing
the orbital "velocity" as a length over a time, even
though, as I have shown in great detail, and as was already
understood long ago, the orbital motion is made up of three
separate velocity vectors. Historically, common wisdom may have
been that there were only two velocities over each dt, but in any
case it was known that the orbital motion is not a simple
velocity.
The calculus
since Newton has been an algorithm that is able to describe a
curve, given x and y changes. What does it find? The differential
calculus finds the slope at the tangent, which we are told is the
velocity at that point. Problem is, I have shown that whatever is
at that point doesn't have a velocity. It has an acceleration, at
the least, and in the circle it has a second-degree acceleration
(three t's in the denominator). So Newton's algorithm must fail.
If it works at all, it can only work on a geometric circle, where
time is not passing. But a kinematic circle is not equivalent
physically or mathematically to a geometric circle, so the
calculus must be reworked.
Now, I have
never claimed that the calculus is wrong, in toto. Newton
was right about most things, and the calculus is a true and
useful algorithm, used correctly. It works great on geometric
curves, and it can be used to find π in a geometric circle. It
solves one of the problems Newton wanted to solve. But as it is
used now, it does not solve the problem of physical circles,
because physical circles are not geometric circles. Their curves
are not equivalent mathematical entities. This being so, I must
show how they differ and how the foundations of circle analysis
must change. Clearly, I cannot do this with raw equations.
Reworking an entire algorithm takes a good deal of groundwork,
and that groundwork requires a good deal of explanation. You
cannot rewrite two and a half millennia of history with a half
page of raw equations. If I want to make a major correction, I
must first convince that the correction is necessary. I hope I
have done that, at the least.
The Greeks
got us off on the wrong track by assuming that the arc approached
the chord as we exhausted the series (Archimedes actually let
smaller and smaller chords approach the circle, in the form of
polygons, but the idea is much the same, in reverse). Newton
and others solidified this error by formalizing it with their
calculi, and Cauchy covered up the error with an even less
physical formalization. For the past 200 years, this error has
been unrecognized because it was unrecognizable. As the
calculus—and thereby the curve—is now taught, no one could
possibly uncover any of this. Both the calculus and circle
geometry are taught as a series of increasingly abstract
equations, not as logical steps, physically grounded. But when
you return to the diagrams, as I have here, it is shockingly easy
to see that circular motion is another big mess.
Quantitatively,
this may be THE biggest error in all of math and physics, since
every single physical equation with π in it must now be thrown
out and redone. The transform π must be jettisoned from all of
kinematics and dynamics.
You may ask
how physics has existed with such errors for so long. Shouldn’t
all engineering be impossible with errors of this magnitude?
Shouldn’t all of our machines immediately break and crash? Not
necessarily. Because we make the same mistakes in all our
equations, the equations are correct relative to each other. Most
of engineering is concerned with relative numbers, not absolute
numbers. For example, it is more important in physics—at least
as a matter of engineering—that we know the how the gravity of
Venus compares to the gravity of Mars, than that we know the real
gravity of either one. If we are wrong about all of them in the
same amount, most of our machines will still work. Only rarely
will a mistake in absolute numbers affect engineering of any
kind. I could show this with specific examples, but I believe it
is clear enough regardless.
Now to sum
up. You should take from this paper several things: 1) There is
no such thing as an orbital velocity. An orbital “velocity”
is actually the summation of three separate and separable
velocities. In the diagram above, the orbital motion is AB - BD +
DC, which is obviously the same as AD + DC. 2) A curve may not be
measured by straightening it out like a piece of string. In any
physical situation, the distance traveled along a curve is found
by running perpendiculars and in no other way. As I have shown,
you do not have to go to any limit: all you have to do is draw
the largest perpendiculars. In the example above, you do not need
to draw lots of little steps and go to a limit: just draw AD and
DC. As long as AB equals AO, AB will always equal AC. 3) The
circumference equation is now C = 8r = 4d. This means that π is
extinct.
All the
thousands of mathematicians who have been chasing more and more
precise values for π have been chasing a phantom. For, although
their equations may be correct in most ways, their assumptions
are wrong. Their first assumption has always been that Newton
understood circle geometry and that he understood how to do
calculus. Mathematicians and physicists since Newton have simply
taken his postulates as true: they have taken his algorithm and
attempted to fine tune it. But the algorithm is faulty at the
foundational level, and has been for millennia. Newton's first
and fundamental lemmae—which are themselves based on the
assumptions of the Greeks—are all false. At the limit, the
tangent is not equal to the chord, as
I have shown elsewhere. The chord is never approached by
either the arc or the tangent, or by any other mathematical
entity in trigonometry or calculus. In creating or measuring the
circle, we are not exhausting polygons, either inscribed or
superscribed, so the chord is immaterial. To create or measure
the circle, we should do it as I have done it here: with
orthogonal vectors. If we choose the correct vectors, we do not
have to approach any limit. We can use a sort of exhaustion, but
we do this only to show that the largest vectors are correct to
begin with. I "exhausted" a process of measurement
above (by increasing the steps along the arc), but this
exhaustion did not take our distance to a limit. It only showed
that, as a
distance,
one path was equivalent to another. Since this was what we were
seeking with the circumference, it gave us a very simple and
quick method. By choosing precisely the right analysis and
interval, we were able to solve without calculus, without limits,
without infinitesimals, without ultimate ratios, and without
integration or differentiation. In a nutshell, I returned to the
pre-calculus analysis of the Greeks, which lay under all modern
analyses. By correcting that analysis in a simple but crucial
way, I have changed and corrected every piece of circular math
and analysis since then. This means that π is now a relic
(except perhaps in scalar equations, like area and so on). Some
will be distraught that so much earnest work has been wasted,
both in mathematics and physics; but rather than hone an error to
the end of time, surely it is better to discover the simple truth
at last.
For
experimental proof of this paper, you may go to Proof
from NASA that π is 4.
Indication I
am correct also comes from the quantum realm, where replacing π
with 4 in quantum equations
explains many mysteries at that level. For instance, in my
quantum spin equations I am able to explain why the proton is
1822 times as large as the electron. But the math only works if
π=4. I have done the same thing in many other places, correcting
Bohr's equations and many other basic equations using π=4.
In fact, I consider this the best evidence in favor of my new
kinematics: it works where π didn't.
Also of
interest to some will be how this impacts Relativity via the
Friedmann Metric. In those papers I show that because the
early equations of Relativity were written as 3D or 4D
Pythagorean theorems, they are falsified by my analysis of pi
like everything else. Einstein and Hilbert and Klein assumed
that objects were travelling on slants in the math when they were
not. In any vector math, including tensor math, all objects are
travelling upon orthogonal vectors, which stand for velocities.

[Addendum,
August 30, 2016:
One of my readers suggested an easy proof of π=4 using a
surveyor's wheel. That is one of those rolling distance
measurers, with a handle. He said that since it was a rolling
wheel, exactly like a cycloid, they must use cycloid math to give
you the number you read on the meter. Since I have never used
one, I checked, and they don't use cycloid math, they use pi.
That's very curious, wouldn't you say? It looks like a cover up
to me. You will say that in measuring a distance—as a surveyor
would need—there is no reason to use cycloid math and every
reason to use pi. In that case, you aren't interested in the
length of the cycloid, you are interested in the length of the
straight line on the ground. True, as far as it goes. But see if
you can follow me on this. What if you are measuring the length
of a curve
on the ground, using a
surveyor's wheel? By using π, you assume the curve is just like
the straight line, and indeed that is what the surveyor's wheel
tells you. But if instead of measuring the length of the curve on
the ground, what if you wished to measure the new curved cycloid
you have drawn in the air with your wheel? In other words, you
have taken a cycloid and wrapped it around a curve. Will the
length stay the same? I suppose the mainstream would say yes, but
the obvious answer is NO. You have just integrated an external
motion into the math, so there is no logical way the length could
stay the same. In other words, you have just imported another
variable of the x, y, z sort, and that variable cannot be zero.
Consult the integral above, which requires a variable for each
constituent motion. The length of the curved cycloid cannot
logically be the same as the original cycloid.
Maybe some of
my readers can grasp that, given that the cycloid is planar
rather than linear. It may help them visualize this. Take the red
cycloid curve in the diagram above and imagine curving the entire
diagram. If you don't see what I mean, think of cutting the whole
curve out with scissors and pasting it onto a curved surface,
like a soup can. After you do that, answer me this question: is
that new curved curve you have created the same as the flat curve
above? No, of course not. If you were writing an equation for it,
you couldn't use the same equation. You would have to write a new
more complex equation, with an extra variable in it to express
the new curvature. Since that new variable could not be zero, it
would necessarily change the length of the curve. Well,
if that is true, then the same logic must apply to any
curve, whether is it wrapped
by a cycloid or wrapped by a simple line. The length of the curve
cannot be measured in the same way you measure a straight line,
since the curve will always have an additional non-zero variable
to integrate into the math. The
length of the curve will always be greater than the length of the
“equivalent” straight line.
Some will
say, “That may be true, but using cycloid math in a surveyor's
wheel won't solve it.” True enough. I didn't mean to imply that
using cycloid math would give you more useful numbers for the
wheel. I meant that using pi and the naive math they do use was a
cover up, since it hid the problem I have just shown you. And I
meant that by using cycloid math, I could show why the surveyor's
wheel must fail to correctly measure any curve.
No doubt many
will answer me, “The surveyor's wheel doesn't
fail, since what a surveyor is
interested in is a simple length, not some mystical kinematic
distance like you are inventing here.” But that is false as
well. Let us say a surveyor is measuring a running track for the
Olympics. Well, he has to measure both the straight legs of the
track and the curves. And what he wants to know is how far the
runners have run, right? Well, running is kinematic. It is like a
little orbit. It requires real bodies to move through the curves.
It is not just curves sitting on the ground, it is curves being
run in real time. Therefore, to calculate the correct distances
through the curves, the surveyor must integrate all the motions
involved. Treating the curves as equivalent to the straights will
fail to do that. And yes, I am telling you the inside lane of the
standard track is longer than 400 meters. Or, the runners are
running considerably farther than 400 meters. This should be easy
to prove by timing groups of top athletes through straights and
curves. I predict it will be found that the athletes appear
to move
through the curves much slower than can be accounted for by
stress on the inside leg, etc. But if you use pi=4 to measure the
length of the curve, this discrepancy will vanish.
In fact, I
find that some tests have been run, confirming this. At this
link to Brigham Young University [p. 25], we find that
“Depending upon the track, athletes may spend up to 60% of the
race on the turn (P. R. Greene & Monheit, 1990).” Holy Cow!
60%? And no one ever thought that was strange? Using π=4, we
would predict 56% of the time to be spent in the curves [4/7.14].
The other 4% would then be given to tighter curves requiring more
leg adjustments. Using running dynamics, you would never predict
a slowdown that great [60/40] in the turns. That's a slowdown of
33%. But if we give most of that slowdown to a mismeasurement of
the curve using pi [a “slowdown” of 21%], it makes more
sense.]
*For
more on this, see my
paper on the calculus.
**For those
of you who have read Dan's critique of this paper at Ex Falso,
you might want to go here
for the rebuttal. I didn't write it, since I find that the
arguments at Ex Falso pretty much fall apart on a first reading,
without the need of any rebuttal from me. And I don't know who
did. I only know the moniker Sleestak from my (old, now defunct)
youtube page, where Sleestak was one of my subscribers. And I had
thought he was there to hear me sing!
If this paper
was useful to you in any way, please consider donating a dollar
(or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me
to continue writing these "unpublishable" things. Don't
be confused by paying Melisa Smith--that is just one of my many
noms de plume. If you are a Paypal user, there is no fee;
so it might be worth your while to become one. Otherwise they
will rob us 33 cents for each transaction.
|