return to homepage
return to updates

Clarification of the equation
a = v²/r

by Miles Mathis

Abstract: I will show the arc and tangent are equal only in one specific place on the circle, and that place is not at zero or the limit. It is at 1/8th of the circle. This being so, we must rework all of Newton's orbital math. Once this is done, I show that we can easily calculate a time for the centripetal acceleration. Yes, the acceleration is not instantaneous, and I can now prove it, by showing you the number for the time.

I was able to continue my analysis of Newton's orbital math by discovering a disclarity between two of my own papers. In my first paper on a = v²/r, I show many problems with the historical proofs, and conclude, among other things, that the orbital velocity cannot be equal to the tangential velocity. But in a more recent paper on π, I show that the tangent is actually equal to the arc. In fact, they are equal not at the limit but at a finite real length. How can these two findings be commensurate?

Well, if we take the orbital velocity as v = 2πr/t, then the tangential velocity cannot equal the orbital velocity. The tangential velocity cannot be expressed that way. Not only is it in the wrong form, it is the wrong number. However, as I made clear in that first paper, the orbital velocity cannot be expressed that way either. So, NEITHER velocity equals 2πr/t. That expression is simply a heuristic ratio that we like, since it is easy to measure from visual data.

However, what I did not make clear in that first paper is that once we find new correct expressions for both the orbital velocity and the tangential velocity, they MAY equal eachother under certain very specific conditions. The tangent DOES equal the arc, provided the tangent is the same length as the radius. In my "Extinction of π" paper, I let the tangent equal the radius in length, and show that the tangent equals the arc.

This appears to confirm Newton and the standard analysis, but it doesn't. The tangent and arc aren't equal at the limit, they are equal only when the tangent equals the radius, in which case the radius, tangent and arc are all equal. Even in this situation, none equals the chord, so my analysis of Newton's lemmae was not wrong. At the limit, the arc approaches the chord, but at the limit, the arc does not equal the tangent. So at the limit, the orbital velocity and tangential velocity are not equal. Newton's proof fails. The current proof fails. The equality of the tangent and the arc can only be proved by making the tangent equal to the radius. Therefore, the orbital velocity is equal to the tangential velocity only when both velocities are "equal" to the radius.

You will say, How can the tangent equal the radius, when one is a velocity and one is a length? The answer: the numbers must be equal. If the velocity is 30, the radius must be 30. But if we match meters to meters, can we just use one second to create the equality? Good question. Another way of asking it is to ask if the number we are given for any radius can be used as a straight velocity in this way. If we are told that a circle has a radius of 5m, does that mean that our velocity along it would be 5m/s? How do the radius and the tangential velocity really relate to one another? I have shown in my π paper that they CAN be related kinematically, but are they NECESSARILY related?

In the case of an orbit, they must be related, since the equation tells us they are. We cannot have an arbitrary velocity at a given radius, we must have a specific velocity. A velocity that is too great will cause escape, and a velocity that is too small will cause a crash. So the answers are yes and yes. The velocity is necessarily related to the radius, and if we get our equations and dimensions right, the velocity should equal the radius. All we have to do is get the time right.

We don't just use 1 second to make the equality, however. Using my new equations, we find that the velocity in orbit is 8r/t. Therefore, to make the velocity equal the radius, we just let the time period equal 1/8 of the orbit. As I show in the diagrams in the π paper, the radius is 1/8 of the circumference; therefore, in 1/8 of the orbital period, the velocity must equal the radius, numerically.

A critic will say, "That doesn't work in real life, as we know from the Moon. Just look at the numbers from the Moon. The orbital speed of the Moon is 1.022km/s, and the radius is 384,400km." Well, it doesn't work because the orbital speed of the Moon is wrong. It is developed from a faulty equation. Let us make all the corrections. If the radius is 384,400km, then the distance travelled by the Moon in one orbit must be 8 times that, or about 3 million km. The orbital period is 2,360,534 seconds. That is a velocity of about 1.3km/s.

My critic will now say, "Even if you are right, the velocity still doesn't equal the radius, numerically or otherwise. The number value of the velocity is 1.3, and the number value of the radius is 384,400." No, I meant to point out a number equality between the radius and the distance travelled by the velocity in 1/8th of an orbit. You see, they ARE the same. The distance travelled at 1.3km/s in 1/8 of an orbit is 384,400km.

In fact, an onboard satellite speedometer, calibrated to work for straight-line distances, will not work in orbit, and engineers know this. That is precisely what caused the Explorer Anomalies. The thrusts were set for velocities as calibrated here on Earth, in straight-line motions, then transformed into orbital motions by the common equations. Since the common equations were wrong, the orbits established from the thrusts were wrong. The satellites flew too high and were thought to be lost.

Not only is the velocity wrong, the acceleration of gravity is wrong. Using the current equations and the value of π, the acceleration of gravity is calculated from an equation that reduces to a=39.5r/t². But the correct equation is 32r/t². Therefore, the acceleration at the distance of the Moon is not .002725. It is .002208.

Some will look at those numbers and say, "That means that using the given numbers for the Moon, in these equations g would not be 9.8, but 7.947!" Well, if you assume that g balances the Moon's velocity by itself, yes. But that isn't the way it works. The Moon is moving in a three-body problem, at its simplest, not a two-body problem. If you calculate that number 7.947, you have left the Sun out of it. To see what I mean, you need to visit my paper where I run the full unified field math on the Moon, showing how the distance and the velocity are caused by Earth and Sun.

As you see, the current equations are hiding many secrets. As another example of a secret being hidden, we can continue to study the arc and tangent. Let us return to the diagram from my π paper:



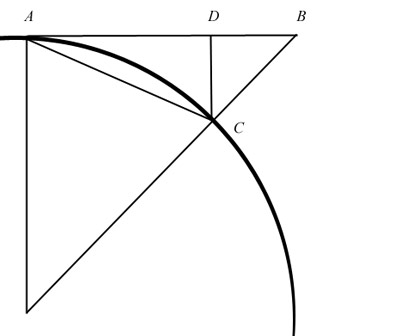
There I proved that AD + DC = arcAC. This means that the tangent equals the arc. This works only when the tangent is equal to the radius, as I said above. The angle at O must be 45^o, so that DC = DB. If the angle is not 45, then the tangent cannot equal the arc, because AD + DC is not equal to AB.

This is important because if we assign the tangent to the tangential velocity and the arc to the orbital velocity, as Newton did, we find they are equal not at the limit, but only when the tangent equals the radius. In fact, as I have shown, the tangent and the arc are NOT equal at the limit. At the limit, the tangent remains longer than the arc. And this means that the tangential velocity and orbital velocity are equal only when the length of the tangent is equal to the radius, or when the time is equal to 1/8th of the orbital period. An orbital velocity found by any other method will get the wrong answer. This is why 2πr/t is wrong: 2πr/8 is not equal to r.

With all this under our belts, we are now in a position to see that we may assign the acceleration a to the line segment BC. Furthermore, if a = v²/2r, and AB = r, then r = v, and a = r/2. Consulting the diagram above again, that is also 2BC = CO. What this means is that we have a new way to find a centripetal acceleration, currently called gravity. The equation a = r/2 gives us a distance of acceleration over 1/8th of the orbit, so the total distance of acceleration over the entire orbit is 4r. Or, we can find the acceleration over any subinterval. Say we want to find the acceleration of the Moon over 1 second. We are given that the period for the Moon is 2,360,534s. Since the Moon is orbiting at 384,400,000m, the total distance of acceleration over the orbit is 4 times that, or 1.538 x 10⁹. Dividing gives us a = 1.538 x 10⁹/2,360,534² = .000276m/s² over 1 second.

For more fun, we can even show that the centripetal acceleration is not found at an instant. If the Moon's acceleration over 1 second is .000276, then an acceleration of .002208 cannot happen over an instant. We can even find the time, with simple math. With the same math, we find that a = .002208 when t = 8s. That is not an instant or an infinitesimal, since it is a calculable number. You cannot have a real acceleration over an instant: we should have known simply from logic that the centripetal acceleration we have always had could not be an acceleration over an instant or infinitesimal. I have just calculated the real time of orbit during the "instantaneous" acceleration, so I have proved that Newton did not go to a limit or approach zero. As I have said in my paper on the derivative, the calculus does not work by going to zero or a limit, it works by going to a subinterval, and I have just shown you the subinterval in a specific problem.

You will say, "But if we can find an acceleration at that small time, we should be able to find an acceleration closer to zero, over an even smaller time." Yes, we can, but that acceleration would not be the centripetal acceleration. In seeking a centripetal acceleration, we are not seeking an acceleration at or near zero time or length. We are seeking the derivative of the orbital velocity, and the derivative of any motion is found by going to a subinterval, as I show in great detail in my calculus paper. We have just gone to that subinterval mathematically, since what I am doing here is calculus without the calculus. I have found the subinterval underneath the orbital motion where that motion becomes uncurved, which is defined as the derivative. And that gives us the acceleration we were seeking. Acceleration is not defined as the change in velocity at or near zero, it is defined as the change in the velocity, period. I showed in my calculus paper that you don't have to go toward zero to find any derivative, and I have shown here in a specific problem that the subchange is always happening over a real interval.

Now you may ask, "But that number, 8s, where is that coming from? You just calculated it, but I still don't get it." Normally, the derivative is found at a subinterval of 1, since that is how it is (or should be) defined. The derivative is not found by going to zero or to a limit, it is found by going to a sub-change or subinterval where we have a constant differential of 1. So normally, we would be looking for a derivative at 1 second. But in the case of the circle, this logic changes slightly. As you can see from the diagram above, I did my "calculus", or my calculations, over 1/8th of the circle. My solution is therefore over 1/8th of the circle. Therefore, to find a solution for the entire orbit, I have to multiply everything by 8. Even the time of the subchange, or what we call the derivative, must be multiplied by 8. That is why the time here is 8 seconds rather than 1 second.

You can see that it took a complete reworking of Newton's postulates to crack open the orbital math, but once I did it, everything began to make sense. We have always been taught that the centripetal acceleration is the acceleration at an instant, but that is illogical. Acceleration, like velocity, is motion, and you cannot have motion at a instant, by the definition of motion. Acceleration is also defined as a change in velocity, but you cannot have a change at an instant. Change requires an interval of change. Motion can only take place over a differential. This being so, we should have been able to find that differential. If the acceleration is not taking place at an instant, it must be taking place over some real time, and we should have been able to find that real time. Problem is, Newton couldn't solve this one, and no one else since then could either. They were looking in the wrong place. They were looking near zero, and the answer was hiding at 1/8th of the circle. The answer is found only when the tangent equals the radius. Because physicists could not solve this, they decided to hide it. Once again, they hid it in the instant. They buried it in the zero and covered it over with centuries of slippery math and slippery explanations. As you now see, the solution is simple.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.