return to homepage
return to updates

Unifying the Electron
and Proton

by Miles Mathis
milesmathis.com
email:mm@milesmathis.com


nope, standard model, wrong again

First posted December 20, 2008
Abstract: Using simple math, I show that the electron is the proton stripped of its outer spins.

This is another of the problems the standard model has failed to solve. QED and QCD do a lot of bragging, but they have very little to say about these fundamental questions. String theory also avoids simple questions like this, although these are the sort of questions a good quantum or atomic theory should answer first. We know that the electron weighs about 1820 times less than the nucleon, but after 90 years of experiment and theory, we still have no idea why. Once again, we have been told that the number 1820 is a fluke or a mystery, beyond physical comprehension, akin to the question of why horses have four legs instead of eight. They do, that is all. But as I will show, the number 1820 is not arbitrary or accidental. It can be arrived at by simple math and postulates.

My explanation begins by importing theory from my paper on superposition. There I showed that the mysteries of light motion and interaction could be explained by stacked spins, each spin outside the gyroscopic influence of inner spins. I showed the existence of four spins, of relative size 1,2,4, and 8, each orthogonal to neighboring spins. In other words, most photons are spinning every way they can spin, axially and in the x,y, and z planes. In my paper on QCD, I applied this to baryons, showing that baryons also had all possible spins. In that paper I unified the proton and the neutron, showing that the difference between the two is only a difference in z-spin. That is, the particle at the center of every baryon is the same. Only the spins are different. I will show in a subsequent paper how this applies to mesons as well. Mesons are these same baryons stripped of outer spins. This unifies all hadrons. In this paper, I will show that the electron is also this same baryon stripped of outer spins. In this way, I will prove that electrons, mesons, neutrons and protons are all the same fundamental particle.

We begin this fundamental analysis by asking how the energy of a particle would increase when it goes from a state of no spin to a state of maximum spin. We start by arbitrarily assigning a non-spinning electron the energy 1. We also assign the number 1 to its radius. We do this because 1820 is a relative number, not an absolute number, so we don't care what the experimental values for mass are. We need only develop relative numbers. Obviously, the easiest way to do that is to start from a baseline of 1.

Next, we let the electron reach some small non-relativistic linear velocity v. That will be our baseline energy for the non-spinning state. To find how much energy the electron could gain by spin, we let the spin match the linear velocity. We let the tangential velocity of a point on the surface of the electron reach v. How much energy has the electron gained? Well, as the radius is to the velocity, the circumference will be to the spin. But we can't use 2πr, since we must be looking at the tangential velocity, not the orbital velocity. 2πr/t applies to the orbital velocity, but we can't use that since the energy of the electron or proton will be expressed mainly through its emitted field, and that field is emitted at a tangent, as a linear vector. We MUST use the tangential velocity here, which is why I have spent so much time in other papers separating the two mathematically and theoretically and developing a new equation for tangential velocity. What we find if we use my new equations is that the circumference is simply 8 times the radius. In kinematic or dynamic situations, we effectively replace π with 4. This gives us a spin energy of 8. We already had a non-spin energy of 1, so the total energy is 9. You may think of the non-spin energy as mass energy, or you may think of it as energy from linear velocity. Either way we must sum the two energies, since the total energy of the electron is a summation of spin and non-spin energies.

To clarify, we use the circumference here instead of the surface area, say, because we want the total energy of a given point on the surface of the electron. That point will have spin energy and non-spin energy. Given an axial spin of the electron, that point on the surface will have a vector at any given dt in one plane only. If we used the surface area equation, that would imply multiple vectors we don't yet have. We don't need to consider surface area until the next step, as you will see.

In this next step, we add the next spin, which is the x-spin. This spin is end-over-end, beyond the gyroscopic influence of the axial spin. Being end-over-end, this spin must have a radius or wavelength of 2. And since this spin is orthogonal to the axial spin, we now have too many vectors to use a simple circumference equation. We must switch to a sort of surface area equation. A point on the surface of our electron will now have a total of three linear vectors, one due to linear velocity, one due to axial spin, and one due to end-over-end motion. To express the total energy of the electron with x-spin, we use this term: [1 + (8 x 16)/2]. The radius is now 2, remember, so the 16 comes from 8r. The 8 comes from the axial spin, which we must multiply by the x-spin. We divide by 2 to express the fact that the particle itself is in the forward part of the x-spin only half the time, so only half the axial energy is affecting the x-energy in any one line of motion. What I mean is that the particle's x-spin will be moving against any linear motion half the time. A spin like this cannot combine with a linear vector by a straight addition. Only half of it can be expressed over any sum.

We repeat this same math and logic to create the y and z-spins. The radius of the y-spin is 4, so the term will be [1 + (8 x 16 x 32)/2²]. We divide by 4 since we must use only half of both end-over-end spins. Likewise, the z-spin is [1 + (8 x 16 x 32 x 64)/2⁴]. We divide by 2 squared squared because we are now in three dimensions. The x-spin is expressing only 1/4 of its strength relative to z, since it is orthogonal twice. The complete equation or representation then becomes:

[1 + 8], [1 + (8 x 16)/2], [1 + (8 x 16 x 32)/2²], [1 + (8 x 16 x 32 x 64)/2⁴]
= [1 + 8], [1 + 2⁶], [1 + 2¹⁰], [1 + 2¹⁴] = 9, 65, 1025, 16385

The electron with all spins has an energy of 16,385. The electron with no spin has an energy of 1. The electron with axial spin has an energy of 9. If we divide 16,385 by 9 we get 16,385/9 = 1820.56

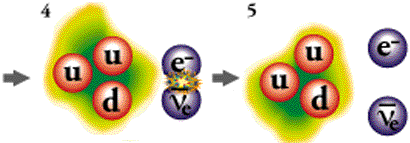
We may therefore deduce that the electron at rest is spinning only about its own axis. An electron with all possible stable spins is a proton, anti-proton, or neutron. An electron with no z-spin is a meson.

This number is very close to the atomic mass unit or Dalton which has a value of 1822. My margin of error may be explained by the presence of the gravitational field at the quantum level, but I will save that analysis for another paper.

I will be asked how the electron can show a wave motion with only an axial spin. I have already shown that the wave characteristic of matter and of light is caused by stacked spins. But here we have only the first spin. How is the wave expressed? Well, it isn't expressed by an electron at rest, and we are comparing rest masses here. The electron must be moving to express a wave. If the electron begins moving and expresses a wave, of course it must have a second spin. It must get this spin from collision with photons in the charge field, we assume. And this second spin will add to the energy and therefore the apparent mass of the electron. A moving electron will become a sort of stable meson. As you can see from the math above, we can predict that it will have an energy about 7.2 times (65/9) that of the electron at rest. So in the first instance, the moving electron is not gaining energy only from Relativity. It is primarily gaining energy from x-spin.

As a bonus, I will now show that the magnetic moment of the electron and its electric charge are the same number. Currently, the two are measured in different SI units, making the comparison difficult. Logically, the two fields—magnetic and electric—should be measurable in the same units, such as Newtons or Joules. They both create forces, so it is the force we would like to compare. But in current theory, we find that the magnetic moment at the level of the electron is measured in J/T, or Joules per Tesla. The electric charge is measured in Coulombs. So going from one to the other is a bit tricky. You are rarely or never told how they compare in size to one another directly. Since this information is highly useful in creating theory at this level, I will show you how to make the transfer.

The charge on the electron is currently measured to be 1.602 x 10^-19 C. The magnetic moment is 9.284 x 10^-24 J/T. Dividing, we find that the charge is 17,255 times the magnetic moment. If we compare the units, we find that J/T may be written as Cm²/s. But how do we develop a transform? We need to know how many meters there are in a second. Fortunately, we can do that simply by using c. We don't know how many meters there are in a second, but a photon does. A photon is going c, so for him there are 2.9979 x 10⁸ meters in one second. Three hundred million meters in every second, which means that, for light, the second is much larger. But we have meters squared here, so if we compare the square meter to the second, we get the number √c, which is 17,314. Therefore that is our transform from meters to seconds. You can see that it almost precisely the right number.

To read about a new experiment that confirms this paper, go here.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.