superposition explained by Miles Williams Mathis

Superposition

by Miles Mathis

Where the master has failed

What hope for the student

Had he obeyed him in all?

—Richard Wagner, Siegfried

First posted October 17, 2005

In this paper I will offer a simple mechanical explanation of superposition. I will provide an easy visualization as well, one that simultaneously solves the mystery of superposition and the wave motion of particles.

Heisenberg and Bohr assured everyone that this was not possible. The Copenhagen interpretation, which is still the preferred interpretation of quantum mechanics by contemporary physicists, states in no uncertain terms that the mysteries of quantum physics are categorically unsolvable. That is, they are not only unsolved, they are impossible to solve. All other interpretations of quantum mechanics have agreed with this interpretation, regarding the impossibility of a straightforward visualization or of a simple mechanical solution. Some variations have denied other aspects of the Copenhagen interpretation, especially regarding its opinion of the collapse of the wave function. Bohm, for instance, has attempted a deterministic explanation of certain parts of QED, including a reinterpretation of the wave function and of the Uncertainty Principle. But not even Bohm or Bell believed that anyone could offer a simple visualization that would explain superposition or the so-called wave-particle duality.

Einstein came closest to this belief. He remained convinced that quantum mechanics would eventually be explained in a more consistent manner. But, again, it was mainly the probabilistic nature of quantum dynamics that bothered him, not the fact that it could not yield to simple visualizations. He did not like God playing dice, but he did not expect God to draw us a picture with every new theory.

I did not approach the problem intending to find a visualization or an easy mechanical solution. I only wanted to make better sense of it in my own mind. But in analyzing the problem I found that the mechanical difficulties were not nearly as formidable as has been claimed. I found that I could quite easily visualize the physical motions, and that I could put these visualizations into pretty simple words and pictures. One basic discovery allowed me to do this, and that is what this paper is about.

I believe that the most efficient way to lead the reader through the problem is to analyze the current explanation of superposition, as it is presented in a contemporary text. As my text I will use David Albert’s Quantum Mechanics and Experience. I choose this book for the same reason that the status quo chose to publish it: it puts the theory in as clear a form as possible, for laymen and physicists alike. Albert is a philosophy professor at Columbia, but he has been embraced and tutored by many mainstream physicists. This book may therefore be taken as a representative, if not perfect, expression of current theory. If it were not it surely would not have been published by Harvard University Press.

Albert begins by taking two measurable qualities of an electron. He tells us that the qualities don’t matter, and that we could call them color and hardness if we wanted to. In a footnote on page 1 he informs the reader that experimentally he is talking about x-spin and y-spin, but he does not elaborate beyond that. Conveniently, this footnote allows me to make my first major substantive point. From a logical point of view, an electron cannot have angular momentum on the x and y axis at the same time—not if both spins are about an axis through the center (Albert claims that they are). Imagine the Earth spinning about its axis. Call that axis the x-axis. Now go to the y-axis, which also goes through the center but is at a 90^o angle from the x-axis. Try to imagine spinning the Earth around that axis at the same time that it is spinning around the x-axis. If you can imagine it, then you have a very vivid imagination, to say the least.*

To see what I mean, remember the gyroscope and the phenomenon called precession. A torque applied to the axis of rotation is deflected, so that circular motion is not allowed about the y-axis. You can have circular motion in only one of the two planes at a time. To see why this is so, think of a point on the surface of the sphere or on the edge of a wheel. Give it spin in the xy-plane. Now follow its course and see the curve it describes. Once you have done that, think of giving it a spin in the zy-plane at the same time. You have a second curve applied to the first curve. But these two curves cannot be added to create a new curve that the body can follow as a whole. If the body were free to follow both curves from the first dt, then the first thing it would do is warp very badly. Very soon it would be twisted beyond recognition. But real bodies are not free to warp into any shape possible. They already have structure at many levels, and this structure is rigid to one degree or another. So if you try to apply a second circular motion to a real body, you are applying a force that does not just lead to motion—you are applying a force that is trying to break the body itself. It is the molecular bonds themselves that are resisting you. The body does not want to warp. This is why you can apply a second spin to a liquid in circular motion. The liquid does not resist the second orthogonal force. But your second force ends up destroying the “body” of the circular motion, which in a liquid was just a pattern anyway.

That said, it is possible to have simultaneous x and y spins, but you must apply the second spin to a center outside the object. What I mean is that the electron must spin end over end, rather than spin about the axis through its center. To go back to the Earth example, you can see that we can easily imagine the Earth hurtling end over end throughout space, since this end over end motion would not affect its axis spin at all. A gyroscope resists a 90^o force, but only because we have fixed the center of the gyroscope relative to the force. A gyroscope will not spin in two ways about its center. But if we put the gyroscope in a spherical container, then we can rotate the gyroscope around a point on the surface of the sphere. We can do this even if the gyroscope is firmly attached to the container. Take a spinning bicycle tire and extend the axle out so that the diameter of the axle is equal to the diameter of the wheel. Attach the ends of this axle firmly to a great sphere with the same diameter, so that the wheel is inside the sphere. You can now rotate that sphere about any point on the surface of the sphere, without the internal motion causing precession. This is because you are no longer attempting to cause two different rotations about the same center. You have created a center just beyond the influence of the first axis.

What is even more interesting is that the circle of this new revolution now has a center that is not stationary—it travels. And it travels in a very interesting way. Let us say you have the Earth spinning about the x-axis, and you give the center of the Earth a constant velocity in the y-direction. Next, we add an end-over-end spin in this same y-direction. Now, what sort of total curve would this end over end spin create, for the center of the Earth? It would create a wave.

[To see an animation of this wave motion, you may take these links. The first is a windows media file, the second requires Quicktime (and is much faster to download). wave.wmv 4.5Mb. wave.mov 780kb. Expect to wait 30 seconds for the wmv file. Thanks to Chris Wheeler for use of these files.]

Let that sink in for a few seconds. Albert assumes that both angular momentums are measured about the same center. Beyond that, he assumes that the measured qualities or quantities don’t matter. He assumes that angular momentum is conceptually equivalent to velocity or position or any other parameter. He assumes that because that is what all physicists have so far assumed. What matters for QED is how these unanalyzed variables plug into equations. I have just shown that the actual variables matter very much. The whole explanation for QED lies in the real motions of these real bodies, and the explanation is capable of being stated in simple, direct terms, as I did it above. The two angular momentums not only influence eachother in specific and distinct ways; the ways they influence eachother provide the conceptual and physical groundwork for QED—a groundwork that has so far been ignored.

But let us return to Albert’s argument. He gives the electron color and hardness, to simplify the analysis. The electron then has four states: black, white, hard, soft. The physicist has equally simple tools. He has a color box and a hardness box. If he feeds in an unknown electron, the color box tells the physicist black or white. The hardness box tells him hard or soft.

Now, if the physicist feeds white or black electrons into a hardness box, half trip the hard detector and half the soft. Likewise for hard or soft electrons fed into a color box. This means, according to Albert, that “the color of an electron apparently entails nothing whatever about its hardness” or the reverse.

The problem encountered by Albert’s physicist is that these two simple detectors seem to work in strange ways, if you set them up in combination. If the physicist sets up three boxes like this: color box, hardness box, color box, the percentages at the end are mystifying. The hardness box in the middle is set up so that it captures only one emerging color, which Albert lets be white. The white electrons travel to the middle hardness box, where half of them make it through and go to the last box. The surprise is that of those, only half are white when they come out. Our final color box finds half of them are black. Wow. Albert and QED tell us this is a big problem. It cannot be explained logically. Albert says that his physicist tries everything. He builds his boxes in a variety of ways, to make them more (or even less) precise. It doesn’t matter. The same 50/50 split comes out at the end.

This has been one of the central problems of quantum physics from the very beginning. It has been a mystery for at least 80 years. But the outcome is easily explainable once you have my analysis above in hand, regarding the various spins. Let’s say you have a sample of electrons and are going to measure angular momentum in both zx and zy planes. If we have four possible outcomes, then we assume that each momentum is either clockwise or counterclockwise, relative to some observer. Now, put yourself in the position of this observer and see what happens. At the first moment, you look and you see that the electron is rotating clockwise about its x-axis, with that axis pointing straight at you. This means that the rotation is in the zy-plane. In other words, you are looking at a little clock, since it is moving relative to you just like the second hand on the face of a clock. That clock face exists in the zy-plane. A moment later the electron has rotated a half-turn, end over end along the x-axis. This rotation is in the zx-plane, about a traveling y-axis. After this half-turn, you look again at the clock face. Its motion is the same, but it now appears counterclockwise to you.

If that was confusing, you can easily perform the above visualization with a desk clock, provided of course that it is not digital. Hold the clock in front of you. Its hands are turning clockwise, and they represent the spin in the x-plane. Now give the entire clock a spin in the y-plane, simply by turning it one half turn end over end. If you do this you will now be looking at the back of the clock. The second hand is now moving counterclockwise, relative to you. It is that simple. That is all I am saying. The second hand of the clock is spinning around an x-axis that is pointed right at you. Then you spun the whole clock around a y-axis. Very elementary, but it shows us that the x-spin of the electron must be variable, if you measure it relative to an observer external to the electron. If the electron has both x-spin and y-spin, then the x-spin will be variable, measured by a stationary device. Only an observer traveling with the electron would measure its spin as consistently CW or CCW. The same thing applies in reverse, of course. If you are measuring the other angular momentum, then you get a periodic variance in the first one.

You could say that the spin changes due to relativity, but that would actually be over-complicating the situation. We don’t need any transforms here, and the kind of simple relativity I have just described was known long before Einstein. It is true that my analysis used relativity to find a solution, but it is the simplest, pre-Einstein sort of relativity. It is just to say that an observer must pay attention to how the object he is measuring is changing over time. A measuring device, whether it is an eyeball or an electron detector, is a constant frame of reference, and a spinning electron will show variance with regard to that device at different times, as I have just shown. There is nothing esoteric about it, although I suppose it is a subtle thing to have to notice.

Once we apply this to our measuring devices, whatever they are, we see that this must affect our outcomes quite positively. Let us go inside the first box. It was measuring color, so let us assign color to the clock-face rotation. White is CW, black is CCW. The box finds that some electrons are white and some black. To differentiate, it must apply some field or force to them over some dt. Let us imagine, to simplify, that the box feeds the electrons into a chute, like cattle, and then puts them all through the same door. This door is like the metal detector at the airport, except that it takes a picture of the electron as it rushes through. It has a very fast f-stop, an f-stop of dt. If the electron was CW at that dt, then the box ejects it from the white door. If the electron was CCW at that dt, then the box ejects it from the black door.

This is, in fact, very much like the way detectors work. They don’t take pictures, of course, but some sort of force or field separates the white and black electrons. The field may not be limited to a dt, but the first impression of the field is crucial. The electrons are moving quite fast, and the time periods are therefore quite small. The field doesn’t have time to snap a bunch of pictures and start changing its mind.

What this all means is that whiteness and blackness and softness and hardness are not constants. Every electron is both black and white and hard and soft, at different times. But it is all those things only if you sum over some extended period of time. At each dt, it is either hard or soft, black or white. It is not both at the same time. At one measurement, it will be one or the other. Over a series of measurements, it will be both.

This is the subtlety that QED has never penetrated. It explains the above problem like this: If you put electrons like those I have described through a color box, the color box sees some of them as black and some as white over the dt measured. But they are actually not white or black as they come out—they remain potentially both, depending on the point in the wave you measure. If you measured the white ones coming out at a different point in the wave motion, you would find them black, and vice versa. Now, the color determination is repeatable, since a similar box will catch the electrons in similar ways. All color boxes tend to shute and channel electrons in the same way, so that the exiting group is made coherent. A second color box must then read them the same way as the first.

What happens in the second box (the hardness box) solves the mystery. The second box creates coherence in the second angular momentum. This assures that other hardness boxes will find the same hardness. But in creating this coherence, the second box re-randomizes the first variable. Why does it do this? It does this because the wavelength of the two angular momentums is different. If the first wavelength was taken as R, for the radius of the electron, then we have to take the second wavelength as 2R, for the diameter. This is simply because the second wavelength is caused by end over end rotation. If we cohere the end over end rotation, this must split the measurement of the axial rotation. If we cohere the axial rotation, this must split the measurement of the end over end rotation. One is half the other, so you cannot create coherence in both at the same time.

I can show this with simple waves in two dimensions. Study the diagram below. We have two opposite combinations of ½ and 1 waves. If you synchronize the ½ waves, the 1 waves are off. If you synchronize the 1 waves, then the ½ waves are off. You cannot synchronize both. This, in essense, is what is happening in box two. The hardness waves are being made coherent, so that the color waves are being thrown out of synch. The third box then reads them as ½ one and ½ the other.

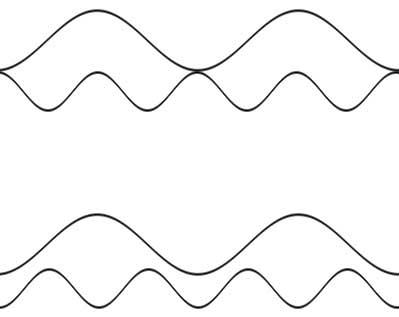
You can see that I have simultaneously solved the problem of superposition and the problem of the wave motion of quantum particles. I did this simply by noticing that the second angular momentum must be about a center that is just external to the object. That is to say, the y-spin is end over end.

With the hindsight this gives me, it seems shocking that this was not seen earlier. The reason it was not seen is that Heisenberg and Bohr convinced everyone early on that Quantum Mechanics could not be explained with straightforward logic and simple visualizations. No one has ever bothered to apply a little commonsense to the physical situation. They were so sure that it couldn’t be done, that they didn’t even try to tackle the problem on a visual or mechanical basis. This predicament soon snowballed, since as more and more great physicists looked at the problem and failed to explain it, later physicists became more and more sure that it couldn’t be solved. They did not want to waste their time combing something that every genius from Bohr to Feynman had already combed. That seemed not just foolish, but sacrilegious. But the fact is that there has probably been no one since Bohr that tried very hard to make classical sense of the problem. Physicists who came right after Bohr took his word for it, and contemporary physicists have reached the point where most don’t even want a mechanical explanation of QED. The spooky paradoxes are more fun. They make better copy.

You may now go to my second paper on superposition, to see a similar experiment solved even more quickly and transparently. That experiment is the famous one of two beam splitters and two mirrors. In that paper I also offer three more diagrams, which may be helpful to many.

A related problem is that of entanglement, which I analyze and solve here.

More recently, I have blown apart the CHSH Bell tests, unveiling the terrible mathematical cheat at the heart of these experiments. This leaves entanglement in tatters.

To see how my solution destroys quantum nonlocality, you may go to this recent paper, which even gives you the new wavefunction equations—including the new degrees of freedom I discovered above.

I think it is obvious that the end over end spin in the y-direction can be applied to other problems, including the propagation of photons, the two-slit experiment, and so on. In subsequent papers I will apply my finding to the electron and proton and to a large list of mesons, to show that the same four stacked spins can explain all quantum make-up and motion. I will also have a lot more to say about other specific problems within QED and QCD, and their solution with straightforward logical analysis.

*Addendum, Feb 2012: A close reader just asked me for clarification on the spins here. He pointed out that the Earth has a wobble in its spin. Isn't that part of a second spin, since it isn't along the original axis? If we continued the wobble, we could create a whole spin in either direction. I answered: Excellent question, and I will even add it to my super.html paper, to clear up confusion. Let's look at your Earth wobble, to get to the bottom of this. The Earth's wobble isn't caused by two spins about two different axes, as in my example. It is caused by a motion of the first axis. We let the Earth spin on z, say, then we move z. Yes, we can actually spin z, moving the north pole to the south, and I think that is what you are getting at. We then have spins in two planes, which seems to prove your point. We could then call the spin of z either x or y, and it looks like I have been refuted. However, I have not been refuted, since we are talking about different things. If you now rename the spin of z as x-spin, your x-spin is not the same as the x-spin I am outlawing. I have outlawed some x and y spin, right? Well, I am outlawing the original x-spin, the one that is the same sort of motion as the original z-spin. Which is a spin about an axis. You have found a spin of the axis, not a spin about the axis. So my point holds. That x-spin about an x-axis is still outlawed. In fact, your new x-spin is the same as my end-over-end x-spin, since if we give the Earth any linear motion, your x-spin will appear end-over-end. North and south poles switching ends is end-over-end, is it not?

He then replied, Yes that clears that up, but there is still the matter of the point of spin. You say that the end-over-end spin needs to spin about a point on the end of z. I have reminded you that we can spin z about its center. What gives? And I answered: I admit that it could be one or the other. Either way creates what I would call an end-over-end spin. But my way allows me to create my quantum spin equation, which answers a lot of questions that have been in the shadows. So the argument for my way is straight from data. The quanta could spin your way, but in fact I don't think they do. The spin equation wouldn't fit data. To be specific, if we let the z-axis spin about its center rather than about one end, we don't get a doubling of the spin radius with each added spin. We need that. See elecpro.html for the spin equation I am talking about. As for the physical reason quanta choose to stack spins that way, by spinning about a point on the end of z, I don't see the answer yet. I suspect that it is some analogue of the centrifugal force, and that the quick first spin pushes following spins out to an "edge." Could also have something to do with imperfect roundness of the initial spin. They have supposedly just shown that the electron is incredibly round, but nothing is perfectly round, I assume. Any imperfection might cause later spins to be pushed outward like this. If anyone has a better theory, he or she can email me with it. I wouldn't say it is crucial, but it would be nice to figure it out.

Update, 2013. I figured it out myself the next time I re-read this paper. To understand why the photon's second spin spins around a point on the original spin surface, we just have to look at the cause of that second spin. I have shown previously it must be caused by collision with another photon. The first photon stacks a second spin on top of the first because it cannot spin any faster on the first axis. It has reached a spin velocity of c, and if it encounters a positive spin collision that would increase its spin energy, it can stack that extra energy on only by creating another spin. Well, since the point of collision is on the outer surface, the photon naturally spins about that point. The second spin must take as its new center that point of collision.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.