return to homepage
return to updates


HOW DO PHOTONS TRAVEL?

by Miles Mathis
milesmathis.com
email:mm@milesmathis.com


art by David Kogan

Abstract: I develop a firm number for the local wavelength of the photon, show how it is created by the spin of the photon, and how this local spin is stretched by the linear motion into the wavelength we see and measure. I prove that the transform from the local wavelength to the measured wavelength is c², showing why this term is found in the famous equation E = mc².

In previous papers I have shown that photons have a number of stacked spins, explaining the mysteries of superposition and so on. But here I will look at the linear motion of photons. I will study how the measured wavelength is caused by the wavelength of the spins, and how different colors are created.

Before we get into that, I would like to give credit to Descartes, who knew that color was caused by photon spins in the early 1600's. I believe he made this proposal in Dioptrique, around 1638. This was before Newton's corpuscles, so the fact that Descartes was able to intuit an answer so close to correct at that time is extremely laudable. If I remember correctly, Descartes got the energies reversed from red to blue, but connecting color to spin was a masterstroke in itself. We will see that color is due to the size of the photon, which is more a matter of radius than spin velocity, but the two are inextricably linked. It is spin collisions that cause the spin radius, so we would obviously have no spin radius without spin. Since I recently published strong evidence against Descartes' theory of reflection by the back surface of raindrops to create rainbows, I felt compelled to add this paragraph to this paper, showing he was also often right against very long odds.

From a previous paper, we know that the radius of the B-photon is G times less than the radius of the proton. This gives us a photon radius of 2.74 x 10^-24m. The z-spin is 8 times the radius, so we should find a basic wavelength of 2.2 x 10^-23m. Obviously, we don’t find photons with a wavelength that small. Why? Simply because the wavelength we measure has been stretched out by the velocity of the photon. The photon would be measured to have a wavelength of 2.2 x 10^-23m only if it were at rest.

You will say, “Even if we accept that the photon is spinning, how can the z-spin be stretched? The spin would give us a spin radius, which is just a length. A length cannot be stretched by motion, unless you are proposing some kind of relativity here.”

I am not proposing relativity as the solution here. The answer to your question is that a spin is not just a radius, and is not just a length. A spin is a motion: a motion that takes time. Even if the photon were spinning at velocity c, one rotation must take some real time. We know that the linear velocity of light is not infinite, so we must assume the speed of spin is also not infinite. If it is not infinite, it must take time. If it takes time, then it will be stretched by the linear motion. While the surface of the photon is spinning, the photon as a whole is moving some linear distance x.

So how much does the velocity stretch out the wavelength? We can discover that most easily by using this simple equation:

E = mc² = hc/λ

λ = h/mc

Let us take an infrared photon, as our first candidate. The mass equivalence of the infrared photon is 2.77 x 10^-37 kg, so we just solve:

λ = h/mc = 8 x 10^-6m

If we compare that to the wavelength at rest, we find the wavelength has been stretched out by a factor of about 3.63 x 10¹⁷.

Since that is very nearly c², we assume that the transform is in fact c², and that the difference is a difference between the size of the B-photon and of the infrared photon. Remember that we developed the at-rest wavelength from the B-photon and the moving wavelength from the infrared photon.

Our assumption is borne out by the numbers, since if we divide 8x 10^-6 m by c², we get 8.9 x 10^-23 m, which is almost exactly 4 times our B-photon wavelength. We may assume that the infrared photon is about 4 times larger than our B-photon.

But why c²? Let’s look at the mechanics, to find out. As usual, nothing esoteric is going on here, so we can analyze just as if we were analyzing pool balls. If the photon is spinning while it is going c, and the radius is being stretched by a factor of c², then that must mean that the photon is spinning at a velocity of 1/c. It takes one full rotation to create a single wave, since the rotation is physically creating the wave. And we want to find one full rotation while the photon is moving 8 x 10^-6m. That will give us the wave we measure. At speed c, the photon goes that far in 2.67 x 10^-14 seconds. So the photon has spun once in that time. By my new kinematic circular motion equations, the circumference is 4 times the diameter, so a point on the surface of the photon travels 8.8 x 10^-23 m. If we divide the circumference by the time, we get 1/c.

Which begs another question: Why would the spin be the inverse of the linear velocity? Because both are dependent upon the same fundamental factor: size. The smaller the quantum is, the faster it goes. The photon goes c precisely because it is so small. It can maximize its speed because it can dodge most other quantum traffic. But this size also determines its spin rate. Notice that we have found it to be spinning extremely fast: 1 cycle every 2.67 x 10^-14 seconds, which is equivalent to 3.7 x 10¹³ cycles each second. That is extremely fast, from our point of view. But, as I have just shown, from the photon’s point of view the surface is moving incredibly slowly: 3 x 10^-9 m/s. That is because one cycle is such a tiny distance. With such a tiny circumference, the photon can move with a tangential velocity of 1/c, and still achieve an astonishing local frequency.

That being true, it still doesn’t provide a mechanical link between c and 1/c. I have shown that the photon can move very slowly, in its own realm, and still create the necessary wavelengths and frequencies we see, but “very slowly” and 1/c are two different things. Why 1/c, precisely? Because, as we know, velocity is a relative measurement, and we are measuring the spin velocity relative to the linear velocity. I will show this with a diagram:

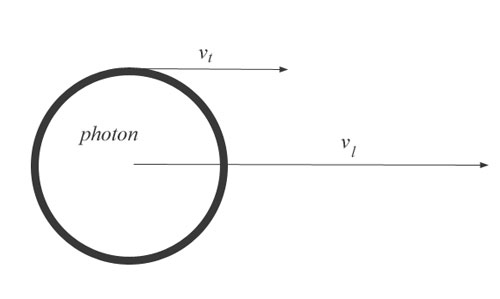
Here we have only the linear velocity and the tangential velocity. I have drawn the linear velocity only a bit larger than the tangential velocity, but let us say we are given a tangential velocity of some magnitude x. We let that magnitude remain constant and we begin increasing the linear velocity. So one line gets very much longer than the other. Obviously, if we make one line very much longer, we no longer need be concerned about the real magnitude of x. We only care about its magnitude relative to the linear velocity. As the linear velocity approaches infinity, the relative tangential velocity would approach zero. This is sometimes called the math of very large numbers, and it allows us to dispense with absolute values. Since velocity is not an absolute value to begin with, this is very easy to do.

You may say that c is not really a “very large number”, but relative to the radius of the photon, it is. We have 31 orders of magnitude between the two, which is a very large number by anyone’s reckoning.

So, as the linear velocity gets larger, the tangential velocity gets smaller relative to it. And the difference between the two is so large that the relationship becomes nearly a perfect inverse relationship. In other words, c² is so large that the tangential velocity can be estimated very successfully with just the transform 1/c.

This also happens to be the reason we can ditch the ½ in the equation E=mc². The two equations E=mc² and E=½mv² are supposed to be analogous, at least when the first one is applied to a photon and the second one is applied to an electron, say. Nearly all the energy of a photon is kinetic energy, so the equation E=mc² applied to a photon is an expression of kinetic energy, with m as the mass equivalence of the photon. But the equation has no ½. The reason it doesn’t is that because c² is so large, ½ becomes negligible. One half of almost nothing is still almost nothing, so we can ignore it as a factor. I explain this in more detail in another paper.

To clarify even further, I will show the math for this. All I have to do is import my new equation which takes us from v to ω. I developed this equation by correcting Newton's orbital equation a=v²/r. Current physics believes that the tangential velocity and the orbital velocity are equal, but they are not. Newton assigns them to different vectors or arcs, and then attempts to show they are equal at the limit. I have shown that his math fails. In my new equations, ω is the angular velocity measured in meters/s, not radians/s, and we can go from v to ω with a simple equation. I used this equation in my paper on the Bohr magneton to show the real radius of the elecron, and to correct the Bohr radius.

ω = √[2r√ v² + r²) - 2r²]

If we insert our numbers for the photon into this equation, using v=c, we get

ω≈√(2rv) = 4 x 10^-8m/s.

That is close to 1/c, so we see that it is not the tangential velocity that is 1/c, it is the orbital velocity of the photon that is 1/c. If we let the tangential velocity of the spin of the photon equal c, then the orbital velocity is 1/c. That is due to this equation, and the fact that the value of r is so small.

And this has other major consequences. It means that Einstein's famous equation must be clarified as well. It now reads E=mc². But I have just shown that the two variable assignments of c in that equation are not equivalent. So, although the equation stands, we must subtly rewrite it. One of the c's is the linear velocity of the particle and one of the c's is the tangential velocity of the spin. This makes the expanded equation

E=mc_Lc_T

Since both values of c are the same, the equation does not change in number outcome, but we now have a much better understanding of what the equation stands for, and what mechanics it is representing. We are squaring c to represent both the linear energy and the spin energy of the particle. The orbital velocity of the particle is 1/c, and this allows us to see how the wavelength is stretched by the linear motion. But when we want to calculate the total energy of the particle, we have to combine the linear velocity with the tangential velocity. This is because the two velocities are straight-line vectors and can be multiplied without a transform. As I have just shown, when the tangential velocity is c, the orbital velocity is about 1/c.

Some will say that I am assuming a longitudinal wave for light, whereas Fresnel proved that light has a transverse wave. If I am able to multiply my local spin wavelength by c² to get a visible wavelength, my local wave must be longitudinal. But that is not correct. Since the wave of light belongs to each photon, via spin, the wave is neither longitudinal nor transverse. Longitudinal and transverse waves are defined as field waves, and light is not a field wave. Light is a spin wave, and the spin is neither transverse nor longitudinal. The local wavelength is just a radius of spin. However, since I have shown (in my paper on superposition) that any electromagnetic radiation must have at least two stacked spins to show a physical wave, this stacking can mimic either transverse or longitudinal waves, depending on the experiment and the effect studied. Fresnel was studying polarization, and although Young had already shown both longitudinal characteristics and transverse characteristics, the polarization experiments seemed to confirm only the transverse part of this duality. And, indeed, polarization can be explained with only the transverse characteristics of the stacked wave. Other experiments and effects are better explained as the stacked spins mimicking longitudinal waves. This is what is happening with Tesla or plasma waves which are longitudinal. In plasmas, the spins beneath the outer spin come into play, and the axial spin of the moving electron is no longer hidden. The charge field coheres or links these inner spins, creating uncommon effects. At any rate, wave theory will not advance beyond its current wall unless it comes to see that both transverse and longitudinal waves are a misconception, built upon a mistaken field wave theory that is an analogue of fluid or sound dynamics. Light waves are not field waves, they are spin waves. Light is its own field, since light is both the linear motion and the spin motion of the photon.

So, I have explained the motion of the photon in a simple manner, providing us with not only a spin but a rate of spin. I have developed actual numbers, first for the radius and mass of the photon, and now for the rate of spin and the tangential velocity and orbital velocity. I have shown how this spin rate creates the visible or measurable wavelength of light. The radius of the photon’s spin creates the actual wavelength, and then this length is stretched out by the linear motion, giving us the measured wavelength of the light.

But now we must move on to ask why and how photons express different wavelengths. Electromagnetic radiation, in the form of photons, comes in a wide range of wavelengths, as we know. How is this achieved? It is achieved by a wide variation of stacked spins. As I began to show in a previous paper, it turns out that photons can maintain a linear velocity very near c over a wide range of sizes. The photon does not reach a size limit that causes slowing until it approaches the spin radius just beneath the electron. At that limit, the largest photons begin absorbing the smallest photons, and the mass increase snowballs. This turns the nearly massless photon into the small-mass electron.

The most common photons appear at the size range of 1821³ less than the proton mass and size. This is where we find the infrared photons, as I showed previously. But the small mass of the photon allows it to stack spins over a wide range of radii. In this, it is unlike the electron or proton. The proton cannot add extra spins above the z-spin without creating instability. This is why “mesons” over the baryon size are not stable. The extra spins begin interfering with the energy of the inner spins. But with the photon this appears not to be the case. Extra spin levels do not cause appreciable slowing, nor do they cause appreciable instability. We may theorize that smaller photons would be more stable, but the difference in small photons and large ones is not easily measured from our level.

What this means, specifically, is that if we give the infrared photon a z-spin as its outer spin, we can find a smaller photon whose outer spin is the y-spin. We can also find a larger photon with another axial or x-spin on top of the infrared’s z-spin. In this way, we find not only stacked spins, we find stacked levels. In other words, we find spins of a₁, x₁, y₁, z₁ and a₂, x₂, y₂, z₂ and a₃, x₃, y₃, z₃ and so on. By this analysis, a₂ has twice the spin radius of z₁. In fact, each spin has twice the radius of the spin under it.

This means that photons do not come in a continuous spectrum. No, they come in stepped levels, each level double the one under it. For example, we found a wavelength of 8 x 10^-6 m for our infrared photon. You will remember that number comes from (c²) 8.8 x 10^-23 m. If we want the next photon larger than that, we double the spin radius to 1.76 x 10^-22 m and multiply by c², which gives us 1.6 x 10^-5 m. There can’t be any wavelength between 8 x 10^-6 m and 1.6 x 10^-5 m. If we measure light with an average wavelength in between those numbers, we must have a mixture of photons. A single photon cannot be found with a wavelength that is in between those numbers. It must have one wavelength or the other.

This explains many optical effects, including rainbows. Rainbows do not have a continuous spectrum, and neither do prisms. We see bands of certain colors. Photons only come in certain colors, and they do not come in the colors in between. In between colors have to be created by mixing photons.

It is known that light is quantized, but no one before me has proposed an explanation of this sort for it. Photons have always been considered point particles, with no radius and no mass. For this reason, it was thought that spin could not be a possible cause of quantization. Therefore we have gotten many complex mathematical explanations of quantization, with no mechanical explanation at all. I have just shown you the simple mechanical cause of quantization.

Addendum: many have asked why these charge photons have not been discovered. My answer is that they have. All the photons we already know about are part of the charge field. The entire electromagnetic spectrum is the charge field. We do not have to propose new photons, we can use the ones we already have. I have given all photons mass and radius, so all photons must cause mechanical forces by contact. This has long been known (see the photo-electric effect) but not fully interpreted.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.