|
|
return to homepage
return
to updates
WHY DOES A
RAINBOW
CURVE DOWN?

by
Miles Mathis
Abstract:
I will show that the current answer is wrong on all levels. Using
Alexander's band and stunning photographic evidence, I will prove
that the curve of the rainbow is caused by a heretofore unseen
phenomenon, one both simple and intuitive. Alexander's band is an
image on a screen of a layer of the corona of the Sun.
Rainbow.
Alexander's Band. This will be the first
in a series on color and refraction. Optics is a very difficult
field, still only partially understood. We are told that Newton
was right about almost everything, but here again that is false.
Newton was sometimes partially correct and sometimes completely
wrong, but he was rarely completely right. Even Newton updated by
Young and Fresnel and Helmholtz and Maxwell and all the rest is
not correct or complete, as we will see here.
First, let
us look at the current answer. We go first to Wikipedia, which
seems to have a manufractured (a typo, but I like it, stet,
and expect to see me use it again) answer for just about
everything. But this time we get zilch. Not even a bad answer or
a link to a bad answer. We are linked to UCAR, the Center for
Atmospheric Research, but we get almost nothing on the curve.
Only this: “The rainbow is thus a circle of angular radius 42
degrees, centered on the antisolar point.” Ditto with the link
to Walter Lewin: nothing good about the curve. So we do our own
search. We find a couple of bad answers at “Ask a Scientist”
at the US Dept. of Energy:
A
rainbow is round because the process is based on angles. Light
from the sun hits the little water droplets after a rain. The
water droplets act like little prisms. Different colors are sent
out at different angles. The sun must be behind you. Imagine a
narrow triangle. The narrow angle is at the water drop. One side
points toward the sun. One side points toward your eye. The drops
for which this device works form a circle. The center of this
circle lines up with you and the sun. If the Earth were not in
the way, a rainbow would be a complete circle. This is why you
can never find "the golden pot at the end of the rainbow".
A rainbow is really a complete circle.
Dr. Ken Mellendorf
Physics Instructor Illinois Central College
This
one was a "toughie". I had to do a little looking. I
had plenty of info on "why" rainbows, but not so much
on "why round" rainbows. This is from Hewitt, Suchocki,
and Hewitt's Conceptual Physical Science, second edition, p 293.
It is published by Addison, Wesley, Longman, copyright1999. (You
might try your local library if you wish to learn more; and if
you want to see the really good diagrams that Mr. Hewitt draws.)
Anyway, here goes: Why does the light dispersed by the raindrops
form a bow? The answer to this involves a bit of geometry. First
of all, a rainbow is not the flat two-dimensional arc it appears
to be. It appears flat for the same reason a spherical burst of
fireworks high in the sky appears as a disk-because of a lack of
distance cues. The rainbow you see is actually a
three-dimensional cone with the tip (apex) at your eye. Consider
a glass cone,the shape of those paper cones you sometimes see at
drinking fountains. If you held the tip of such a glass cone
against your eye, what would you see? You would see the glass as
a circle. Likewise with a rainbow. All the drops that disperse
the rainbow's light toward you lie in the shape of a cone—a
cone of different layers with drops that deflect red to your eye
on the outside, orange beneath the red, yellow beneath the
orange, and so on all the way to violet on the inner conical
surface. The thicker the region containing the water drops, the
thicker conical edge that you look through, and the more vivid
the rainbow.
Your cone of vision that intersects the
cloud of drops that creates your rainbow is different from that
of a person next to you. So when a friend says, "Look at the
pretty rainbow," you can reply, "Okay, move aside so I
can see it too." Everybody sees his or her own personal
rainbow. I hope that casts "light" on your rainbow
query.
Martha Croll
The
reason a rainbow is a smooth curve is because it is the *angle*
between the light incident on a raindrop, and the light exiting
the raindrop, that determines what color is seen. And, as you
note, it also depends on the fact that raindrops are, on average,
roughly spherical. The path from sun to raindrop to viewer's eye
includes the angle, and all the raindrops located so that the
angle has a particular value, will contribute to a particular
color of the rainbow. This might be difficult for a child to
visualize, but it is a simple geometrical notion that you can
demonstrate with a coat hanger. Here is a maybe more detail than
you really want about how it works:
First, some
background: a ray of light that hits the middle of the raindrop
is partially reflected and partially transmitted. The reflected
part goes back directly toward the source; the transmitted part
goes through the raindrop and is partially reflected at the back
surface. Again the reflected part goes back directly toward the
source; the transmitted part leaves the raindrop and we don't
care about it anymore. That ray that reflected from the back
surface is now heading back toward the front surface, where the
partial-reflection thing will happen again—many times, in fact.
On each round trip, some light will be transmitted through the
front surface back to the source.
Second bit of
background: What if the light ray hits off center? Then things
get very interesting. First, the surface of the raindrop acts as
a prism, since the light is incident at an angle, and the light
will be refracted (its path will be bent) as it passes through
the surface. Second, the first reflection from the back surface
will not be in the same place as the second reflection from the
back surface; the light will sort of bounce around within the
drop, reflecting here and there in a very predictable manner and
sequence.
Third bit of background: each reflection from
the back surface will make its own rainbow. Normally, you can
only see the first-reflection rainbow, and maybe a faint
suggestion of the second-reflection rainbow (at a different
angle).
Fourth bit of background: The angle through which
a light ray is bent as it passes through the air-water surface
depends on the index of refraction of the water (and the air).
The index of refraction of water is different for different
colors of light. This is because electrons in the water molecules
are tuned, like guitar strings, and a light ray tries to vibrate
them at the frequency (color) of the light ray. Light rays that
are nearer in frequency to the electron's "tune" are
affected differently—i.e., they see a different index of
refraction—i.e., they are slowed down by a different amount,
and therefore refracted by a different angle—than light rays
farther away in frequency.
So a light ray hitting the
raindrop off center will be refracted, and part of it will exit
the raindrop at an angle that depends on how off-center the
incident ray was. In fact, as the ray hits further and further
off center, the exiting ray will make a greater and greater angle
with the incident ray—up to a point. There is a maximum exit
angle, which corresponds to a certain off-center distance, and
the exiting light is concentrated near this maximum angle,
because the variation of exit angle with off-center distance is
smallest near this angle. You can demonstrate this with a laser
and a cylinder of something clear. The maximum exit angle depends
on the color of light because the refraction angle generally
depends on the color.
Tim Mooney
Then
we find an answer seemingly cobbled from these at Yahoo Answers:
“The reason why the rainbow is curved is because all the angles
in the water drop have to be just right for the drop to send some
sunlight to you, standing on the ground. So, with the sun
*behind* you, only those water droplets that have the same angle
formed by you, the drop, and the sun (this angle happens to be
approximately 42 degrees) will contribute to the rainbow. Other
droplets send their light somewhere else, and if you move to a
different location, new droplets are needed to make the rainbow
you see in the new location. This is why you can’t go to the
end of a rainbow to find the mythical leprechauns and pots of
gold; anywhere you stand, the rainbow is formed by faraway drops
of water reflecting and bending sunlight. The rainbow is curved
because the set of all the raindrops that have the right angle
between you, the drop, and the sun lie on a cone pointing at the
sun with you at one tip.”
All the other answers I could
find on the internet were variations of these, so I suppose this
is state-of-the-art. So let us analyze these before we give the
right answer. Dr. Mellendorf's only sentence that addresses the
question is this one: “The drops for which this device works
form a circle.” That is a statement of fact, though, not a
statement of cause. The question asked is “why is the circle
formed?” Because the device forms a circle is not an answer.
Ms. Croll's answer is also a dodge. She says the rainbow
curves because it is part of a cone, but that is just renaming a
curve a cone. What causes the cone?
Tim Mooney wins the
award for misdirection, however. We get six paragraphs of
“background information” and no answer at all to the question
asked. We knew we were in trouble the moment he put “angle”
in unneeded quotations. He tries to imply that the curve is
caused by the curve of the individual raindrop, but that is
clearly illogical. Then he tells us that it might be difficult
for a child to visualize, but that you can demonstrate it with a
coat hanger. Only one problem: he forgets to demonstrate anything
to us with a coat hanger.
The Yahoo answer may be from
Mr. Mooney as well, since we again get “behind” in
unnecessary quotations of the same kind. And again, most of this
is misdirection about raindrops, which are the current cause of
the refraction, but not of the curve. The only relevant sentence
is the last one, about the cone. But as with Ms. Croll, that is a
description, not a answer. Substituting a cone for a curve does
not tell us anything.
I have to say that it is sad that
these scientists would even bother to post such clearly deficient
and defective answers. Do they really imagine that they have
addressed the question? Does the Dept. of Energy think it is good
PR to have physics seen in this state of undress?
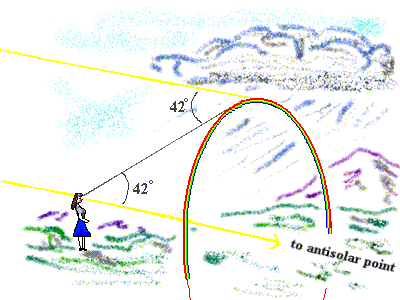
This
is the illustration at UCAR. It was developed from Descartes'
answer from 1637. That's right, we are still using basic rainbow
theory from 1637. The problem is that this angle of 42o
goes to infinity. Why is the
rainbow drawn that distance from the lady rather than three feet
away from her or ten miles away? These people will say that
rainbows can vary in their apparent distance, but according to
this diagram, we should see huge rainbows many miles away. The
clouds themselves, when at a 42o
angle, should cause rainbows.
Current theory has a limit on the Sun's height in the sky, which
limits other factors, but what is the limit on the rainbow's
size? The height of the Sun and the 42o
angle provide no size limit.
An even bigger problem than that comes when we look more
closely at this theory. UCAR has drawn green below red, but they
admit that shorter wavelengths are refracted by different
raindrops than the raindrops that refract red. Red and green
can't be coming from the same raindrop, and they realize that. If
all the colors we see were split by each raindrop, then red would
be below green. So they tell us the lower raindrops refract green
to us and the upper ones refract red. That appears to be an
ingenious solution until you remember that patches of rain don't
come in sheets a single drop wide. Look at this illustration I
made:
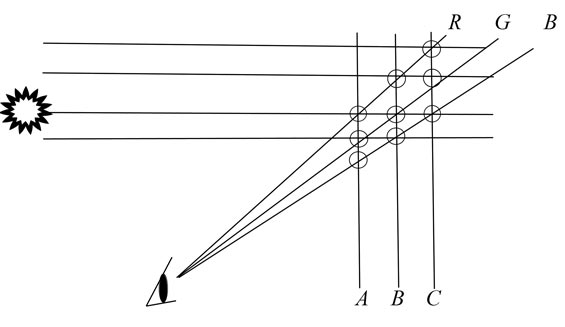
Where
do we see the rainbow? At position A, B, or C? I will be told,
"All three, and the rainbow will just be more saturated."
Maybe, but that doesn't explain why rainbows often look very
saturated with very little rain in the air. Just look at the
picture under title, chosen by Wiki to adorn its own page due to
the saturation of the bow. But the bow is just as saturated near
the ground, where there appears to be very little moisture. It is
clear as a bell down there. The saturation seems to be a function
of something else. It also doesn't explain why rainbows are so
steady. They don't shimmer or wobble and the face doesn't shift
even in high wind. It is easy to postulate a leading wall of
moisture that is not flat to us, due to wind or other turbulence,
or evaporation, or other effects. If the position is determined
by the leading raindrops, shouldn't we see a tilted band under
some conditions? Why is the rainbow so steady, even under
turbulent conditions like a thunderstorm? And why does it always
appear flat to us, as if it is aligned to gravity? I have no
doubt that the color is created by the medium, but the position
of the color seems strangely undetermined by the medium.
A
greater problem for the standard model occurs when we look at the
curve. Imagine instead a rainbow with no curve. Just draw a
rainband in the sky with no curve. Can this be explained with
their 42o
rule? Yes. All the red
raindrops at the top can be explained as having a 42o
refraction. You just have to
postulate that the outer raindrops are a bit further away. Why is
that impossible, according to them? Why should all the raindrops
you see be equidistant from you? Can we not imagine sheets of
rain that set up this way relative to you and your Sun position?
Of course we can. So why do we never see straight rainbands? What
they have done is sneak in an assumption as an explanation. They
say, “If the refraction angle has to be constant, and if the
distance to the raindrops has to be constant, then we will see a
curve.” Yes, true, but that doesn't explain why the distance to
raindrops has to be constant. Yes, we appear to see the raindrops
in a cone of visibility, equidistant from our eye. But again,
why? A description is not an explanation.

Here's
a photo that proves the current explanation is false. You can see
that the photographer has turned to take a picture of just one
leg of the rainbow. The Sun is no longer behind the photographer,
relative to the “cone of sight”, and this is clear from
looking at the light on the mountain. The Sun is now on the left
shoulder of the photographer. Ask yourself this: if the image of
the rainbow is dependent on the cone of sight, shouldn't the
image be flat to the viewer on both ends, and not just in the
middle? As we turn to focus on one of the legs, we should see it
flat to us. Instead, we see it flat to the Sun. The whole rainbow
is always in single plane, no matter how close or far away it is
to us, or how much we zoom in on one leg with a camera. This
despite what we are told about the rainbow being different for
every viewer. But that is a big lie, one you can test yourself
very easily. The rainbow isn't even different for you as your
turn your head or as you move around. You can walk quite a
distance relative to a rainbow, and it doesn't change at all. It
stays right where it was, as if it is part of the landscape. This
fact conflicts most aggressively with the current explanation,
since the rainbow is supposed to be a function of your cone of
sight. If the rainbow is a function of the cone of sight, the
rainbow should move against the far background as you move. But
it doesn't. This is one of the great mysteries of rainbows, and
always has been, and yet the historical explanation utterly
ignores it. No, you can't walk over and find where the rainbow
hits the ground, without making the rainbow disappear, but you
can certainly "uncenter" yourself to it. If you
couldn't, then the two legs of the rainbow would move as you
moved. They don't. In many regards, the rainbow acts like an
image on a screen. Your own position is generally set, but not
definitely set. If the rainbow was a function of your light cone,
as we are told, then your position would be definitely set.
Which brings up another theory-ender. You don't really
have a cone of sight, do you? What you have, according to this
strange theory of sight, is a sphere
of sight all around you. All
points equidistant from you form a sphere. The cone they are
talking about is formed when this sphere intersects a plane. The
sheet of rain is supposed to be this plane intersecting your
sphere, creating a cone. Unfortunately, that would mean the sheet
of rain would have to be at a 90o
angle to you and the Sun.
Otherwise you would see one leg of the rainbow nearer to you. The
current guardians of theory will say, no, it only means the
raindrops you see as colored are in that plane, but that brings
us back to the earlier problem: why would you see rainbows or
raindrops only in this cone of visibility, when you don't see
other things that way? You don't see only things that are
equidistant from you. You can resolve lots of different objects
at lots of different distances, so this cone of visibility is
just a mirage. They are still trying to sneak in an assumption as
an explanation. They get you thinking that to see something, all
the photons have to arrive simulaneously, but that is absurd.
I
like to say that problems are not as hard as they seem, but I
will admit that this one is deep. It didn't come to me on the
first try. In fact, it didn't come to me until I looked closely
at Alexander's band. Alexander's band is the dark band between
two rainbows, named for Alexander of Aphrodisias, the
Aristotelian of the third century AD. Many rainbows are doubled,
with the outer rainbow opposite in color to the inner. This is
now explained as due to a second path of refraction inside
raindrops, but I will show in other papers that this is also
false. At any rate, the dark band in between the two rainbows is
explained as a gap between the two phenomena: that is, as a gap
between the raindrops refracting with three inner bounces and
those refracting with four inner bounces. Unfortunately, like all
else, this explanation of the dark is completely illogical. We
are told the band is dark because we are seeing refracted light
above and below, coming from the raindrops. But this would only
explain increased light within the rainbow itself. It cannot
explain increased darkness in the band. We only have to look at
real rainbows to see that the light variations around the rainbow
are not explained by the current theory.
In fact, the
explanation of the darkness of Alexander's band and the
brightness inside the rainbow is some of the worst of current
theory. As for the latter, we are told by Wiki:
The
minimum deviation angle for the primary bow is 137.5o.
Light can be deviated up to 180o,
causing it to be reflected right back to the observer. Light
which is deviated at intermediate angles brightens the inside of
the rainbow.
Amazing
how versatile those little raindrops are. They always manage to
explain everything with a new refraction or reflection angle. So,
according to current theory, at the center of the rainbow the
raindrops are reflecting light right back to us. Then, from 180o
to about 140o,
we also get get a “deviation” that causes white light, and
this deviation causes just as much brightness as a straight
reflection (since the rainbow is not brightest right at the
center: the whole center is equally bright). At about 140o,
we start to get color. From 138o
to 129o
we get no refraction,
reflection, or deviation, or at least none that can reach our
eye. From 129o
to 127o
we get a four-breaker
refraction inside the raindrop, causing a reverse rainbow, and
then below 127o
we again get some brightening,
but not as much as from 140o
to 180o.
It is beyond belief that such pathetic theories are ever
published or taken seriously by anyone. Leaving aside the
question of color creation for later, we only need to ask why a
spherical raindrop would increase brightness by reflecting or
deviating light to us from 140o
to 180o,
and from 127o
to 0o,
but would not send us any extra light from 138o
to 129o.
Interference is supposed to be creating supernumerary arcs, as we
will see in the next paper, but Alexander's band is not supposed
to be an interference phenomenon. It is supposed to be caused by
“minimum deviation.” As evidence of this, we are sent again
to Descartes, and his 138o
red refraction (same as 42o,
measured from the other side). That is the minimum deviation of
the inner color band, as you see in the illustration from Wiki.

Problem
is, that is just a limit of this three-bounce refraction, it is
not a limit of all other possible reflections and deviations.
Light can reflect off the back of the raindrop in a single bounce
at any angle, depending on where we let it hit in the
illustration. We can also get reflection or deviation in a
two-bounce hit, scattering light at any angle. So this minimum
deviation is just a misdirection. There is no minimum deviation
at 138o,
except for the color red as created by three bounces.
A
further problem is that current theory is basically using
scattering theory to explain color creation, but the two are
opposite. If a single raindrop can cause so many different
refractions, including a one-bounce reflection at any angle from
90o
to 180o,
a two-bounce refraction over a wide range of angles, a
three-bounce refraction over many angles, and a four-bounce
refraction over many angles (plus other bounces) what we have is
scattering, not refraction or “deviation.” As is known,
scattering causes white light, not colored light. So this theory
of three and four-bounce refraction isn't even consistent. This
becomes really clear when they start pushing the theory to
explain Alexander's band. They are trying to make the same
raindrops cause brightening via scattering, and cause color
splitting via refraction. Unfortunately, media don't work like
that. The prism doesn't work like that. A prism doesn't brighten.
It either reflects or refracts, but cannot do both in the same
position. If it is reflecting, it is not refracting, and vice
versa. For this reason alone, the raindrops cannot be the cause
of brightening. If they were scattering, they wouldn't be causing
color, since scattering turns color to white. And they can't
scatter at some angles and cause color at other angles, via the
same turning of forward light.
The same applies to the
minimum deviation for the outer color band. The current theory
tries to create a limit there, but there is none, except
(perhaps) for four-bounce color. At all angles, we will have an
equal probability for single bounce and double bounce reflection
or deviation or scattering or whatever you want to call it. So
this part of the theory is garbage.
Just look at this
quote from the same page at Wiki:
The
minimum deviation angle for the secondary bow is about 230o.
The fact that this angle is greater than 180° makes the
secondary bow an inside-out version of the primary. Its colors
are reversed, and light which is deviated at greater angles
brightens the sky outside the bow.
What?
Just consult the last illustration above, which is right next to
this text at Wiki. You can see the angles of "deviation"
yourself. You may ask the author why angles of 230o
to 232o
create color, but angles of
232+ create brightening. How can one angle be defined as
refraction and the angle right next to it be defined as
scattering? This is the same mechanism! Shouldn't the angles
above violet create ultraviolet, according to any logical theory
based on the historical models? Ultraviolet rays would not
brighten the sky. Since we can't see them, they would actually
darken it, comparatively.
Also notice that, using the
current theory, Alexander's band is explained as the natural
brightness of the sky, without any brightening by the raindrops.
But either my photos or any study of rainbows will show that
isn't true. Alexander's band is the darkest part of the sky, and
we can confirm that by looking at parts of the sky where no rain
is in the air. The moisture “wall” is never running across
the whole sky in front of us, from horizon to horizon. How could
it be? So it is usually easy to compare Alexander's band to parts
of the sky unaffected by the rain. That fact is, Alexander's band
is not a lack of brightening, it is a darkening. It is darker
than inside the inner band and outside the outer band, so that
the current theory doesn't even address the facts. Even if the
theory had a leg to stand on, as a matter of refracting angles,
it wouldn't explain the facts. Alexander's band is not a gap
between brightening, it is a darkening.

To
explain the band, we need to return to the photos. Here is a
beautiful picture showing that the whole inside of the rainbow is
lighter than the rest of the sky. This is an extreme example, but
all rainbows show this effect to some degree. The darker the rest
of the sky is, the easier it is to see the difference in
brightness. Here's another stunning example. You really feel the
Sun inside the bow, and have no problem believing that this is
reflection of the Sun itself. Not a "creation" of the
Sun, but an actual "picture" of the Sun and its corona.

Here
is a picture from my reader Michael Steinbacher, showing the same
thing:

Here's
a closeup that shows the amazing contrast inside and outside:

And
in this photo we see that the sky outside the two bands is also
lighter than the Alexander band, though not nearly as light as
inside the rainbow.

Here
are two amazing photos one of my readers just sent me. Russell
Taylor in Chesterfield, England, has graciously allowed me to
publish them.
 
He
wanted me to be sure to mention that the nearest parts of the
rainbow seemed to be very near him, whilst the upper parts were
further away, causing a twisted bow. He said the phenomenon was a
bit difficult to read, since he was basing the distance of the
middle part on nothing but expectation. But the whole rainbow
could have been much nearer. This tends to confirm my comments
above, but we will look at it more closely later.
For now,
let us return to the contrast shown in the previous pictures. I
will show in an upcoming paper that this lesser contrast is what
makes the outer rainbow less vibrant in color. Yes,
it is the bands of dark and light that cause the rainbow, not the
rainbow that causes the bands of dark and light.
But to prove that I have to
first show that the circles of dark and light are caused by some
so-far unseen phenomenon. If these circles of light and dark are
causing the rainbow, as I claim, what is causing the circles of
dark and light?
It turns out that Descartes was
completely wrong. Rainbows are not caused by a refraction of
sunlight by a triple bounce inside a raindrop. Nor are the colors
split in the way claimed, with red being refracted by different
drops than violet. That is all just a fairly ingenious myth.
The Sun is commonly behind us at certain angles, it is
true, but that is because the rainbow is primarily a reflection
of the Sun cast upon a field of moisture or dense atmosphere from
behind. A
bright patch in the far sky acts as a reflector, and the dense
atmosphere in between acts as a screen. We are seeing a cast
image of the Sun in the sky. In this way, we see that Alexander's
band is actually an image of the least luminous band of the Solar
corona. Study this picture:

On
the right side of the image (straight from Wikipedia), peaking at
about 2 o'clock, you can easily see a band formed. The band goes
all the way around, but it is clearest on the right side. About
halfway to the edge of the corona, you have a fairly distinct
line, separating the corona in half. It is darker inside this
band, and lighter outside. The corona is at a much higher
temperature than the surface, and this is commonly known. What is
less commonly known is that the corona, despite this higher
temperature, is not as luminous as the Sun itself. It is not as
luminous simply because it is less dense. The Sun has more atoms,
and therefore more emission. The solar atmosphere nearest the Sun
also creates a band of relatively low temperature called the
temperature minimum. Here, the temperature drops to about 4,000K,
which by solar standards is quite cool. Above that, the
atmosphere heats back up to around 20 million K, which is even
hotter than the core (see my paper on magnetic
reconnection and coronal temperatures). Therefore, we have
three layers here: the very hot Sun, then a cooler layer, then a
very hot corona. As we see from the photos, this creates not only
bands of heat, but bands of brightness. Just as with the rainbow.
And if you study the width of the middle layer here, you will
find it matches the relative width of Alexander's band!
In
this picture, we find that the middle band of the Sun is about ¼
the radius, or a little less. If the band is 1 inch, the radius
is 4.25 inches, according to my measurement. This is exactly the
width of Alexander's band, relative to the radius of the inner
rainbow. Measuring from the other rainbow photos I have published
here (and from others on the web), I get 8.5 to 2, which is a
match. Alexander's band is not caused by a gap between
refractions, it is caused by the Sun's corona layers. Here is
another photo that shows it,

though
it shows it clearly only on top. We can't see the ring all the
way around in this rather poor photo, but we can see the width of
the band. Again, it is precisely the right width to match
Alexander's band.

The
Moon also has an Alexander's band, as we see here, although it
appears to be wider than the Sun's and is probably caused in a
different way. But since the Moon is also lit by the Sun, we can
assume that the Moon's band is also a reflection of the Sun's
corona. The band is probably widened by the curvature of the
surface of the Moon. You can see all three brightnesses, with the
Moon itself included. The darkness of Alexander's band could not
be clearer.
Here is a third corona image from the Sun,
for good measure. Again, you can see Alexander's band most
clearly from 12 to 4 o'clock, and can even see how it affects the
large flare at 4 o'clock.

I
will be told that the width of the temperature minimum is only
about 500km, which doesn't match the width of the band in these
photos. That is true, since the band in these photos is much
wider than that, being about 300 times too large. Even if we
include the rather cool chromosphere, which extends to about
2,500km, the band is still 60 times too narrow. However, since
what we are seeing is brightness, not heat, the brightness band
would not be expected to match the temperature band. Remember,
although the atmosphere gets hotter as we go up, it loses
density. This density loss would translate into less brightness.
So we have to combine the two factors.
A reader has
complained that even combined those two factors can't give us the
band we see in these photos. He dismisses the dark band as an
"artifact of the poor tonal range" of the photographic
process. My reply was that in the creation of a rainbow on a
screen of rain in the atmosphere via rear projection, we also
have a poor tonal range. Think of the rainbow as an image in the
sky, just like a photo on a plate or on film. Due to the method
of production, the image has low contrast and low resolution,
hence "a poor tonal range." This might not only
increase the apparent width of a dark band in the image, it would
decrease the contrast between dark and light bands (see below for
more). For this reason, it is not what is taking place in the
real corona that matters to our image; it is what is taking place
here in our own atmosphere. Even if you want to call the band an
"artifact" of the process, it would nonetheless create
a real effect. As long as it creates the dark band, by whatever
process, it would be enough to explain what we see, by my new
mechanics (see part two of this paper).
Of course this
means that the curve of the rainbow is just the curve of the Sun
itself. We are seeing an image of the Sun cast on the atmosphere.
This is why it is higher or lower depending on the height of the
Sun. But it has nothing to do with your cone of sight. The
rainbow is larger or smaller, appearing closer to you or further
away, depending on the relative positions of the bright
reflecting place way in front of you and of the patch of thick
atmosphere that is acting as a screen.
As proof of this,
let us look at some more photos. Photos are wonderful, and
honestly, it is photos that have allowed me to get beyond
Descartes and the rest of ossified theory in this case. I am not
standing on the shoulders of giants so much as standing on the
shoulders of photographers (all of whom I would like to thank).
Let's start with several that show the reflecting point in the
background. Pictures from falls are great for this.

This
first one is a close-up, but the rainbow here is actually not
very big. It is close and small. This is because the reflection
point behind is not far away: it is the bright area seen in the
picture, the white in the falls. White means the light is being
reflected back, and it is reflecting an image of the Sun. Notice
the rainbow is most vibrant near the white. The colors fade as we
move away from the white reflecting area. That is why the
photographer focused on this leg of the rainbow. The white is the
reflecting surface, and the mist is the screen. The image is cast
from behind, and then the image goes through the mist. So the
mist acts as both screen and prism. The mist does cause the color
like the prism, but it does not bounce it three times using the
Descartes process. I will show the creation of color in my next
paper; I am only showing the creation of the curve here,
remember.

Here's
another from Niagara. You will say that the least color is seen
with the most white behind, but here that is due to a lack of
mist up high, at the top of the arc. The mist isn't up there, so
it doesn't matter how white the light is behind. The thing to
notice is that the rainbow is not very big, and that is because
the white reflecting area isn't very far away from the rainbow.
The image hasn't had room to spread out after the reflection.

Here's
one that proves my point very nicely. We can almost see the body
of the Sun inside the rainbow, and we can see the white
reflecting point on the far horizon. That is why the rainbow is
so large: the distance between the reflecting point and the bow
is great, allowing for the image to expand before it reaches the
screen.

Now
look closely at this one (again straight from Wiki), which I have
posted as large as possible. We have such detail here we can even
see the radial details of the corona, where the rays shoot out.
We can clearly see a line moving out from the center. How does
the current theory explain this? It can't. No theory of
interference can explain radial lines. This is like a slide of
the Sun's corona projected onto a screen in the sky.
Yes,
the rainbow is, first and foremost, a rear-projected image of the
Sun onto a screen of moisture in the atmosphere. This layer of
moisture acts as both a screen to cast the image upon, and a
refracting medium to cause the color. But the light must come
from behind, because the light must travel through the medium in
order to be refracted. Just as light must pass through a prism,
light must pass through the layer of moisture, in this case
coming toward us from behind the screen.
We have visual
proof of this from this photo of Paul Goldstein:

The
thing to notice there is the cut-off where the shadow intrudes.
If we use current theory, that is unexplainable. If light from
the front is being turned by water drops as Descartes said, how
could the rainbow simply end there? You will say the rocks are
blocking the light from the front, but they are blocking only a
part of it, or that shadow would be black. If we weren't getting
light from that shadowed area, we wouldn't be able to see it at
all. So, logically, it should only be a dimmer rainbow were are
seeing, not a complete cut-off. The cut-off is explainable only
by the rear reflection of light. The rainbow not only requires a
light source, it requires a bright
rear source,
like a movie projector. The falls provide that above the cut-off
line, but not below. Although white water is reflective, it does
not have an albedo anywhere near unity. So the reflected light
below the cut-off line will be much dimmer than the front light.
That is what explains the cut-off of the rainbow.
This is
of paramount importance, because it shows that current theory has
never been an analogue of prism theory, although it claimed to
be. Prisms do not refract light back toward a viewer. With the
prism, refraction was always defined as the turning of light at
an angle of less than 90o.
A reversal of light, or a turning at an angle of greater than 90o
was called a reflection. A
prism can do both. It can reflect with no color, or refract with
color. But it can't do both through the same face. If you are
receiving refraction, you cannot be also be receiving reflection.
And the prism never scatters or brightens.
Rainbow
theory, as taken from Descartes, has tried to sell this
three-bounce, 138o
turn as a prismatic
refraction, causing a color split. But technically, this turn is
a refraction plus a double reflection from surfaces, not a triple
refraction. And technically, reflections do not cause color
separation. It is not clear that Descartes' description was ever
viable, even according to classical theory. And according to
current photon theory, as updated by people like Feynman,
refraction does not just happen at surfaces. The math of
refraction is limited
by surfaces, but cannot be
explained by surfaces alone. It is an interaction with matter
itself, and matter itself is not confined to surfaces. Therefore,
the raindrop cannot be considered to be an empty sphere, with
reflective surfaces. The raindrop may be able to both reflect and
refract, as the prism can, but it is not clear that it can
refract backwards. If it reflects from a back surface, it doesn't
split into color; and if it splits into color, using both front
and back surfaces, like a prism, then the light should pass
through the back surface, being bent but not reflected.
My
mechanics bypasses all that, since according to the evidence I
have presented, the light IS refracted, but since it comes from
behind the sheet of rain, the refraction is a bending, not a
reflection. This matches prism theory and data. The whole sheet
of moisture acts as the medium, not just a single drop.
That
said, my color creation will be just as revolutionary as my curve
creation, through bands of dark and light. I have shown that
these bands of dark and light cause the rainbow and the colors,
not the reverse. The curved bands are primary, and the color is
secondary. In my next
paper, I will show that Goethe was right in his contradiction
of Newton. In many effects, it is not material edges that cause
diffraction or refraction, it is darkness and lightness alone. I
will prove this by showing you that we can look at bands of black
and white and grey on a flat computer screen through a prism, and
obtain color splits from that. This will require a complete
rewrite of not just rainbow theory, but color theory in general.
I will rehabilitate Goethe's theory of color, but I will do so
without deposing Newton. As I have done before in other debates,
I will be able to synthesize both sides, taking the best parts of
both.
I will answer a good question from a reader before
I finish. This reader found my use of rear projection to be a
nice correction to mainstream theory, but couldn't accept the
corona as cause of Alexander's band. His problem was that the
orders of magnitude in brightness differentials aren't even
close. In other words, the differences between the different
bands in the Solar Corona are too great to cause the bands we see
in the sky, which show much less contrast. It is a good
complaint, I admit, but I refuse to think that the width of
Alexander's band is just a coincidence. Therefore I sought an
easy solution to his problem, and I believe I have found it.
Again, it has to do with the rear projection. The difference in
magnitudes would be expected to be tamped down by the far
reflection itself. Remember, in my theory, what we have is not a
mirror in the distance, giving us a strong or near perfect
reflection. We only have a patch of white as our reflector. This
patch of white is usually just white rock or cloud or water or,
at best, snow. None of these things would be expected to maintain
the original contrast differentials in the reflection. Therefore,
I propose that the brightness differentials are tamped down
mainly by that mechanism. Since the reflection is taking place in
the lower atmosphere, very near the ground, the thick atmosphere
will also help to diminish the constrast. And of course the patch
of rain that is causing the rainbow would act to tamp down the
contrasts a third time.
Addendum,
February 2014. Thanks
to links from a reader, we can now include the quadruple rainbow
as proof of my mechanics.

In
2011, National
Geographic published
this photo from
Michael Theusner, claiming it was the first photo ever of the
quadruple rainbow. They used mainstream theory, as above, to
explain it, where light rattles around in a raindrop in four
different ways or more. But while you would expect their
explanation to match that at Wikipedia exactly, it doesn't:
As
a ray bounces around inside a droplet, some light escapes and is
split into its constituent colors, forming a rainbow. Each time
the ray gets reflected, the light, and thus the rainbow, gets a
bit dimmer. When this happens three or four times, the final rays
exit in the direction of the light source—the sun—and create
extremely faint rainbows opposite the original two, which can be
seen only while facing away from the sun.
Seeming
to realize that bows three and four can't be explained with more
internal bounce paths, they explain them with second
"reflections." Or I suppose that is what they are
saying, it is hard to tell. "When this happens three or four
times" is difficult to assign, since the authors are not
trying very hard to write in a clear and precise manner. I assume
what is happening three or four times is happening in three or
four separate raindrops. It can't be happening in the same
raindrop, because then you would have three or four three-bounce
reflections in one raindrop, which would be something like 12
deflections. This also wouldn't explain the different positions
of the third and fourth bows. If these reflections are happening
in the same drop, then the bows would be superimposed. But
letting what is happening three or four times happen in separate
raindrops can't work for them either, because if it is happening
more than once, what is happening in the second drop isn't what
happened in the first drop. What I mean is, for the light to go
from the first drop to the second, it must already be coming back
to the eye. The first drop already reflected it, so it is already
moving toward the eye (and Sun). Well, if that is so, then when
it hits the second drop, it can't be reflected in the same way.
It it were, it would then be going away from the eye, and
couldn't be seen. It can only be refracted
in the second drop. That
already proves my theory, which is a theory of refraction, not
reflection. To get bows in four places, they can't have two or
three or four reflections. They have to have some refractions in
there. But once they start admitting refraction instead of
reflection, they have just shot their own theory. They just have
the light doing whatever they want it to at each juncture, and
then they throw all the contradictions in theory out the window.
But in my theory, the rain always acts as a diffuse prism,
refracting at each and every juncture, but never strictly
reflecting (when color is created). Color can't be created by
reflection, as I showed, so I don't use it to create any of the
bows.
Although the four bows are impossible to explain
sensibly with current theory, they are easy to explain with my
theory. You need at least two major sheets of water, each one
creating a new refraction. This explains why the bows are in
different places: the sheets of water are different distances
from the eye, so of course they will create different angles
relative to the eye. It also explains why the bows are in sets:
the first set is created by the two edges of the Solar Corona, as
I showed above. The second set is created by refracting the first
set through a second sheet of water. This changes the position
and also creates a reversal. Consult this diagram from my second
paper on rainbows and prisms:

That
diagram was borrowed from the mainstream, and it shows that
prisms in sequence are known to cause this reversal, with no
reflection involved. You can see that it would also cause an
apparent change in position, since the light is bent.
[Thanks
again to all the great photographers whose work I used. I didn't
find photo credits on the web, or I found web monikers. If you
want a photo credit for your work, just drop me an email and I
will add a tag to this paper, and also a link to your own page if
you like.]
Go
to part 2, where I show how color is split (and where I also
rehabilitate Goethe and his optics).
Go
to part 3, where I show a new explanation for the white
rainbow, or fog bow.
If this paper
was useful to you in any way, please consider donating a dollar
(or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me
to continue writing these "unpublishable" things. Don't
be confused by paying Melisa Smith--that is just one of my many
noms de plume. If you are a Paypal user, there is no fee;
so it might be worth your while to become one. Otherwise they
will rob us 33 cents for each transaction.
|