|
return to
homepage
return to
updates
Explaining
Mesons without Quarks
by
Miles Mathis
First posted December 27,
2008
Abstract: I show that mesons may
be explained by stacked spins, without quarks or chromodynamics.
I do a full analysis of the muon, the pion, the kaon, the tau,
the D meson, the eta meson, the charmed eta meson, the bottom eta
meson, the Z particle, the muon neutrino, and the tau neutrino.
Also additional theory for neutrino oscillation.
I
have promised an analysis of mesons and I now make good on that
promise. To make the best speed through this paper, a reader
should have already read my papers on
superposition and on the electron/proton
unification. He or she would also do well to read my
paper on QCD.
In my superposition paper I first
showed that any spherical particle could be shown to have four
stacked spins, those being an axial spin plus the x, y, and z
spins. Each spin is orthogonal to neighboring spins and outside
the gyroscopic influence of other spins. Applying this simple
analysis to the photon, I was able to explain the various
mysteries of light propagation and interaction, including the the
so-called paradoxes of detectors in sequence and so on. I
dissolved the wave-particle duality, showing that it was
explainable and visualizable in mechanical terms. This also
dissolved the Copenhagen interpretation, which is now a relic.
In my paper critiquing QCD I showed that the neutron and
the proton were the same particle, with different stacked spins.
I showed that a neutron can be made into a proton simply by
reversing its z-spin. This explains beta decay by a
straightforward mechanical process.
In my paper unifying
the electron and proton, I showed that a proton stripped of the
three outer spins would have precisely the energy and mass of an
electron at rest. This explained the number 1821 in a mechanical
way, showing all the spin math.
Here I will show that
mesons are protons or neutrons stripped of the z-spin, or
electrons with superadded middle spins. I will show why mesons
come in a variety of energies and how these energies are
composed, using only stacked spins. I will also show why mesons
are not stable.
In my paper unifying the electron and
proton, I found a basic meson state at 1025/9 = 113.9 times the
energy of the electron at rest. This is an electron with 3 spins,
or a proton missing the z-spin. This gives us 113.9 x .511 MeV =
58.2 MeV. That is not the energy of any known meson, so my first
task is explaining how to arrive at a known meson from this
number.
The Muon
Let
us start with the muon, with a mass of 105.7 MeV. The muon is no
longer considered a meson, but it is actually the primary and
fundamental meson. It is the most stable meson, and it is the
most stable because
it is the most fundamental. It is simply the electron with three
spins. It lacks only the z-spin. If it had a z-spin, it would be
a baryon. If you go to my paper on electron/proton unification,
you will see that I have mathematically and mechically derived
the values of the four fundamental spin levels, and the muon
inhabits the third level, with no other complication but the one
I will now explain.
The first thing to notice is that
105.7 is almost twice 58.2, so we will proceed by postulating
that the muon is double the third energy level (for some reason
yet to be discovered). Even if that is so, I still have too much
energy in my derived and predicted number of 116.4, and that is
because that number includes the emission field. In my paper on
the electron/proton unification, I started at unity by assigning
the non-spinning electron the number 1. I assigned no number to
the emission field, so all my numbers in that paper included it.
In other words, my foundational theory postulated the particle
and its emission as a single number, but experiment measures only
the particle and its spins. In experiment, the emission escapes
into the field (except with the neutron and other neutral mesons
that trap the field). The muon has a charge and is not neutral,
therefore its emission is not measured to be part of its mass or
energy in experiment. This is the difference between my initial
number and the number of experiment.
Let us develop a
number for that emission field. In my paper on QCD, I developed
an energy for the summed emission field of the baryon. It is
simply the mass difference between the proton and neutron. The
neutron traps this energy and the proton emits it. This energy is
in the amount of 2.31 x 10-30
kg. But this energy is a field, so it must be denser if emitted
from a smaller radius. The y-level has half the radius of the
z-level, so by the inverse square law the field will be 4 times
as dense. Relative to the particle itself, it will not have
gained mass or energy, but relative to a measurer, it will. An
equivalent energy in a smaller space must appear to gain mass.
For the same reason, the loss of the z-spin will double the mass
of the field once more, since the z-spin was orthogonal to the
y-spin. As we saw in the electron/proton unification paper, only
half the z-spin multiplies with the y-spin. Not only the particle
but also the emission must move against the linear motion half
the time. We divided by 2 when we added the z-spin, so we must
multiply by 2 when it is stripped away. This gives us a total
increase of 8 times. [A shorter way to arrive at this 8 is to
notice that the z level has 8 times the energy of the muon level
(16385/2049). But here we are looking at the emission field, not
the spins of the particle. The two fields act in a reverse way.
The total energy of the particle increases as we go to outer
spins. The energy of the emission field increases as we move in.
The emission field becomes denser as we get nearer the surface of
the particle, while the spins get more energetic as they gain
more radius and torque. But both fields follow the same radius
and change in the same way, in reverse. So if the spin field
increases eight times, the emission field decreases eight times].
If we multiply 8 x 2.31 x 10-30,
we get 1.848 x10-29,
which is 20.29 x the electron mass, which is 10.37 MeV. If we
subtract that amount of emission from my theoretical number, we
get 116.3 - 10.37 = 105.9 That is near enough to the muon mass
for my rough method here.
But why is there no neutral
muon? By my mechanical theory of stacked spins, a neutral
particle is a particle whose spins trap the emission. The neutron
does this by creating a total spin path that sends the emission
back to the particle (see illustration below). The emission
cannot escape and becomes part of the mass of the particle. This
is why the neutron weighs more than the proton. But the muon
cannot create a path that comes back to the particle. We require
four vectors for that, and the muon has only three. This is also
why the muon has no stable state. The y-spin is the outer spin of
the muon, and this spin must always be othogonal to the line of
motion. The y-spin cannot match the linear motion, nor can it be
opposite to it. So we cannot have a forward moving charge,
creating stability, nor a reversed charge, creating neutrality.
This missing neutral muon is convincing evidence in favor of my
stacked spins. You can see that my theory has a simple mechanical
explanation for it. Ask the standard model why there is no
neutral muon.
Finally, why is the muon twice the third
energy level, instead of inhabiting it exactly? I don't know at
this time. It may be that the muon is actually two fundamental
particles, this fundamental particle being the true meson. The
muon may be a meson/anti-meson pair. Or, I may still have my 2's
in disarray. My math contained an error of two (which is still in
my book) and it may still contain one.
The
Pion
Now let us look at the pion,
another common meson. The energy of the pion is about 139.6 MeV.
In my previous
paper, I showed that the electron with axial spin only was
the electron at rest (or low speed). To show a de Broglie wave
motion, the electron had to move at a certain speed and
experience collisions in the field. At this speed it would
develop an x-spin and gain the energy of that spin. With both
spins, the electron could express the wave in a simple mechanical
way. I showed the energy of the electron with x-spin was 7.222
times the energy of the electron rest mass. I said that in this
way the electron at speed was a sort of stable meson (since both
x and y-spins could be called "mesonic" states). In the
same way, I showed that the electron with y-spin would have 1025
its rest energy. The electron with axial spin was the rest
energy. If we divide 2049 by 7.222 we obtain 283.7, which
(multipying by .511MeV, the energy of the electron at rest) is
145 MeV. So, as a matter of stacked spins, the pion is the muon
times 9 divided by 7.222. Mechanically, we may imagine that the
pion is created by a collision orthogonal to the direction of
linear motion, stripping the baryon of z and x spins
simultaneously, but momentarily boosting the y-spin. This boost
is achieved by a linkage between the y-spin and the axial spin,
as we see from the math. This is not difficult to postulate or
visualize, since without the intervening x-spin, the a and y
vectors would naturally link. Nor is it difficult to imagine a
collision that would target x and z levels, since they are also
linked as vectors.
This would also explain why a pion
quickly becomes a muon, and why the muon is more stable. The muon
has all inner spins, at natural levels. It only lacks the z-spin.
It has a normal level of charge protection, although this charge
is moving orthogonally to the linear motion, and therefore cannot
express its full character. The charge field also lacks a z-spin,
stripping it of its largest defense. Therefore the muon is not
stable. But the pion is even less stable, since it is missing the
x-spin as well as the z-spin. It is momentarily more massive,
since it has gained energy from the collision. But this mass
cannot be maintained, since the fields that could absorb it are
gone. The pion tries to rebuild as a muon, funneling energy down
from y to x, but it cannot do so. As the pion collapses, it
pauses momentarily at the muon energy while the rebuilding is
attempted and failed, then, like the muon, it dissolves. It, like
the muon, must dissolve either into an electron with axial spin,
which we can detect; or into an electron with no spin, which we
cannot detect. We will not detect the failed particle until it
benefits from collision and re-establishes itself as a spin
particle (or forms a multiple and becomes a neutrino—see
below).
Now, we only need explain the difference between
145 and 139.6. Fortunately, this gap is the same relative size as
my gap with the muon. We had a 10.37 MeV gap with the muon, and
we have a 5.4 MeV gap with the pion. That is near enough to 2 for
this paper. The pion is larger, so by my math and theory, we
would expect a smaller gap. The gap is caused by the emission
field, so how would we expect the emission of the pion to differ
from that of the muon? The pion is missing the x-spin on the
emission. This means that it is missing one of the 2's in the
math. Even though the y and a-spins are augmented by the
collision, the y-spin has no x-spin to double beneath it (see the
full spin math in
my previous paper for clarification here).
The
biggest problem with the pion is found in the neutral pion.
Experiment gives us an energy of about 135 for the neutral pion,
and that cannot fit my theory at all, at first glance. I have
proposed that neutral particles block emission, so that the mass
of the emission must increase the mass of the particle. A neutral
pion should act like a neutron, swallowing its own emission. This
would make it weigh more. The neutron weighs more than the
proton, not less. So the neutral pion should weigh more than the
charged pions. A neutral pion should weigh 145, not 135. But this
also has a simple mechanical explanation. Blockage of emission
can only take place if the emission travels through the four
spins and obtains a final trajectory that takes it back toward
the particle. This is what happens with the neutron, as I showed
in my analysis of beta "decay". But the pion cannot
create this path. It lacks x and z spins. It has only a and y
spins. Even though the a and y spins are augmented, they still
cannot create the path in the right way. We have mechanical
vectors at all points, with nothing esoteric or hidden, so if we
want to explain a different energy, we must do so directly, with
a clear visualization. The answer lies in the easily demonstrable
fact that a particle with only a and y spins will funnel the
emission back to the particle, but the emission will miss the
particle (see illustration below). Therefore, the emission is in
vector opposition to the linear motion of the particle, but it is
not "re-absorbed" by the particle. If the particle is
moving in the +a direction, the emission will be summing in the
-a direction; but since it is missing the particle, its energy
cannot be added to the total. Its energy must be subtracted from
the total. This is why we subtract the 5 MeV instead of adding
it. Instead of 140 + 5, we obtain 140 - 5, which gives us about
135.
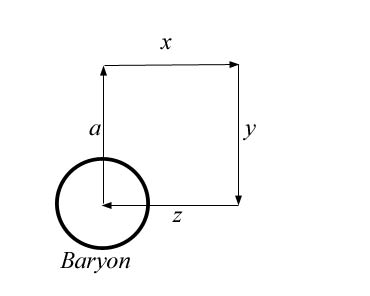
with
only a and y vectors, the pion's emission misses the
particle
(the particle is also moving +a)
[In
imagining the loss of x and z vectors in the illustration above,
you must not allow the a and y vectors to line up, so that y
points right back at the particle. This is because this
two-dimensional illustration is missing the third dimension. In a
three-dimensional schematic, the a and y vectors would not in
fact line up. The illustration here is a useful visualization in
some ways, but it is not complete or completely accurate.]
The
Muon Neutrino
I proposed above
that muons and pions must dissolve either into electrons with
axial spin or without. We know what an electron with axial spin
looks like, since I have proposed that this is the normal
electron at rest. But what is an electron with no spin? In my
paper on electron/proton unification, I showed that the
non-spinning electron would have a mass of 1/9 that of the
spinning electron. But do we ever find such a particle? We
wouldn't expect to find it by normal methods, since the normal
methods use E/M fields, and the non-spinning electron would have
neither charge nor magnetism. But watch this: If we divide the
current energy of the electron .51MeV by 9, we obtain .05678.,
which is 56.78 keV. Still not ringing a bell? Well, the energy of
the muon neutrino is 170keV. If we divide 170 by 56.78, we get
exactly 3. There is no muon neutrino. The muon neutrino is three
non-spinning electrons huddling together for protection, each one
trying to block the charge wind in one of the 3 dimensions. These
electrons have no charge or emission, so they do not repel
eachother. They cannot repel any other particles either, so they
get pushed into groups like this, where their only repulsion is
from the strength of their shells or surfaces.
All
neutrinos may be explained by other means. Here I have shown that
the muon neutrino is three non-spinning electrons in a group. In
my QCD paper, I showed that the electron neutrino was a variation
in the charge field caused by a z-spin reversal. The tau neutrino
will be lost below in the same way, to a simple mechanical
explanation.
Neutrino
"Oscillation"
I showed
at the end of my QCD
paper that neutrino oscillation is actually a change in the
B-photon or
emission field, not the reincarnation of one particle to another.
But here I give the muon neutrino to an electron triplet. Which
is it? Both. In neutrino oscillation we go from one unseen flux
to another. We call the first flux an electron neutrino and the
second a muon neutrino. But in reality, the first flux is a flux
of the B-photon
field, with no neutrino present. The second is a flux of the
electron field, with electrons colliding with free neutrons and
losing their axial spins. Again, there is no neutrino present,
but there is a new particle present after the second event: an
electron triplet. In each stripping, a neutron is stripped of its
z-spin and multiple electrons are stripped of their axial spins.
It would appear that it takes three electrons to strip each
neutron. The axial spin has a much lower energy than the z-spin,
and only by adding their linear energy to the equation can the
moving electrons successfully attack a neutron. I will have more
to say about this in other papers.
The
Tau Neutrino
The tau neutrino has
been called a neutrino simply because the standard model had no
other way of categorizing such a small meson. The tau neutrino
has an energy of 15.5 MeV. That is about 30 times the energy of
the resting electron. If we bring an electron up to speed, it
will gain an x-spin and thereby a wave. I have shown that this
x-spin will give the electron 7.222 times the energy of the
resting electron, which is 3.69 MeV. You can see from both these
comparisons that the tau is about 4 times the x-spinning
electron. So it turns out that the tau is another multiple: it is
four x-spinning electrons. But why would x-spinning electrons
join in groups of four?
As it turns out, the x-spinning
electron has a number of states, and only one of these states is
stable. That is the electron we measure when we measure an
electron with a wave. In this state, the emission is summing in
the same direction as the linear motion. To say it another way,
the linear vector and the x-vector match. This gives the moving
electron a protective charge field in front with its full
numerical value, and allows the electron to repel other
electrons.
But this is only one of several possible
states. In all analyses up to now, I have assumed that the
electron had only four total vectors, and I have implicitly let
the linear vector match the axial vector. But now I must include
the further complication that the axial and linear vectors may be
orthogonal. If this is the case, we will have to analyze not four
but five orthogonal vectors in every baryon. For instance, let
the electron spin about a y-axis. The emission will be thrown out
mainly in the xz plane. If we let the electron now move in x or
z, then the linear motion and the emission will match, in a
vector sense. But if we let the electron move linearly in y, it
will be moving orthogonally to its own emission, you see. It
would not be stable, because it would have no protection from the
emission. This unstable x-electron is the component of the tau
neutrino.
To say it another way, the particle is moving
forward and emitting sideways. The x-spin is unstable, and would
tend to decay back to the axial level or lower. This is how we
get the tau neutrino. The tau neutrino is four x-spinning
electrons, all of the unstable variety, and all different from
the others. By setting themselves up this way, the unstable
x-spinning electrons are able to to become stable. The tau
neutrino is emitting up, down, and to both sides, and has a
charge weakness only directly ahead of it, where there is a
minima. For this reason, it is stable, but not as stable as an
electron. I have called all these constituents of the tau
neutrino electrons, but I think it is clear that two of them are
positrons. To be precise, I should say that the tau neutrino is
made up of two electron/positron pairs, orthogonal to one
another.
I should also come up with a better name for the
tau neutrino, since I have now shown that it is not a neutrino.
There are no neutrinos. I will call it the quirino for now. In
honor of Majorana, who came so close to solving the problem of
gravity. It is close to quarto, but I don't want quarto since it
is already overused.
The Kaon
In
experiment we find that a kaon in decay can yield either pions or
muons. This was the hint I needed to discover its construction.
The most stable kaon is very long-lasting, living for some 10-8
seconds, and weighing about 493.7 MeV. Two charged pions and two
muons give us almost 492 MeV. The long life is given it by the
muons. They add stability to the kaon, making it much more stable
than other mesons composed only of pions (such as the eta meson,
below, which lives only 10-19
s). Pions and muons both emit sideways, which allows them to
huddle in groups of four, either with one another or with with
themselves. We have four charge orientations at the y-level, and
one particle in the quadruplet represents each orientation. The
kaon therefore emits to all four sides, missing only the forward
emission (relative to its linear motion). The lack of forward
emission makes the kaon a meson, and keeps it from having
stability. But the partial muon construction protects it in
collision, since the muon has all inner spins.
The
Eta Meson
The eta meson is clearly
just 4 pions. It is either 3 neutral pions and a charged pion, or
2 neutral pions and 2 charged pions. This would give us either
about 545 MeV or 550 MeV, depending on the combination. The eta
meson is 547.8 MeV in experiment. Currently the eta is said to
decay into three pions, but the trackers are missing one of the
pions, due to the orthogonal vectors. It is almost impossible to
track orthogonal vectors simultaneously in such a complex decay.
Charmed Eta Meson
The
charmed eta meson is another meson that matches my equation
outputs almost precisely. You will have noticed that my
fundamental meson states are all multiples of 2. The charmed eta
resides near this level: [1 + (8 x16 x 32 x 64 x 128)/29]
= 65,536. We divide by 9 to achieve a multiple of the electron,
and then multiply by .511, which gives us 3721 MeV. As with the
pion, we only need one more factor, and that is 7.2222/9 (see
above). This gives us 2986 MeV. The charmed eta meson in
experiment is 2980. From this we may conclude that the charmed
eta is related to the pion, each of them losing inner spins in
collision.
Bottom Eta Meson
The
bottom eta is another meson created like the pion and charmed
eta. We have a fundamental meson level at [1 + (8 x16 x 32 x 64 x
128)/28] =
131,072. If we divide by 9, we obtain 14,560, and if we multiply
by .511, we get 7,442 MeV. If we multiply by 9/7.222, we obtain
9273 MeV. The experimental value of the bottom eta is 9300 ± 40.
Like the charmed eta and the pion, the bottom eta is missing
inner spins after a collision from the side.
The
Tau
The tau has been a very
difficult particle to isolate in experiment, and that is because
it is a complex combination of mesonic states. It decays into at
least one muon, and this fact helped me a bit to discover its
make-up. As I showed above, pions commonly decay into muons, as
they shed unstable outer spins. So we should look for the pion in
the tau. The tau was also a difficult particle for me to explain,
since it is the first example I uncovered of a baryon huddling
with a meson. In this case, we have two unstable baryons huddling
with two pions.
Let me first explain the unstable baryon.
In my QCD paper I offered 16 baryon states, assigning eight to
neutrons/anti-neutrons and eight to protons/anti-protons. This
was a complete list of stable
baryons, but it is not a complete list of baryons. We have 16
more unstable baryons. The mechanical reason for this goes back
to my analysis of the tau neutrino, where I show that the
emission field of any emitting particle may be emitted sideways.
I showed that if we include the linear motion as a fifth vector,
this vector may be orthogonal to the outermost spin. Since the
spin does not emit in the same direction as the linear motion, it
does not provide full charge protection. So the baryon may be
emitting to any of four sides, all of them orthogonal to the
linear motion. If we combine these z-spins with inner spins, we
obtain 16 more states. All of these 16 are unstable. This gives
us a total of 32 baryon states, and that number can be arrived at
easily by summing the five possible vectors. With five vectors,
we must have 25
possible states.
The tau makes use of two of these
unstable baryon states. You may imagine that these two opposite
baryons meet back to back, trapping two pions in the other
corners. In other words, if the baryons are emitting north and
south, the pions emit east and west. This gives the tau a split
second of stability, until the baryons begin to turn and face
eachother. The intervening pions prevent this turn for an
instant, but they are overwhelmed by the energy of the baryons,
and the structure quickly collapses. The pions become muons, and
the baryons strip eachother of spin completely, decaying back to
spinless electrons, and becoming invisible to our detectors.
But there is one other complication. The baryons are
doubly unstable, due to a recent collision. Just as pions are
damaged particles, lacking inner x-spins, the baryons in the tau
are damaged baryons. They have been hit from the side, losing
this same x-spin. It is as if the particle has been crushed in a
vise, by a field orthogonal to its main motion. This orthogonal
field targets inner spins. So we multiply by that same term we
have seen before with the pion: 7.222/9. This term express a loss
of the x-spin, and a linkage of the a and y spins. So take the
baseline energy for the baryon [1 + (8 x16 x 32 x 64)/24]
= 16,384, divide by 9 to find a multiple of the electron and
multiply by .511. This gives us 930 MeV. Then we multiply by
7.222/9, to express the collision or vise. This gives us 746.6
MeV. Doubling that to express two particles gives us 1493. Two
charged pions gives us 279.2. Adding them all together, we have
1772. The energy in experiment of the tau is 1777.
To sum
up, we have two baryons and two pions, both damaged from the same
sideways field or collision, and all missing the x-spin. They
combine in a NSEW square, and then quickly decay.
The
Z particle
Using my meson
equation, we can find a value for the Z. The Z is a baryon with
several unstable spins forced on top of the stable z-spin. It is
always found in high-energy accelerators, so it must be a product
of collision. I have rewritten this section based on later
calculations I did in my Higgs
papers of 2012. It is my current opinion that the Z is three
particles in collision, all of them multiples of the proton. Here
is the primary equation: [1 + (8 x16 x 32 x 64 x 128 x 256)/214]
= 524,289. That is very nearly 219.
We then divide by 9 to achieve a multiple of the electron, and
then multiply by .511, which gives us 29.8 GeV. If we double that
again, we get 59.5GeV. If we divide the first number by 16, we
get 1.86GeV. If we add them all together, we get 91.16GeV, which
is the energy in accelerator of the Z. This means that the Z is a
level 20 proton meeting a level 19 proton and a level 15 proton.
This analysis overwrites my previous analysis.
The
D meson
"Meson" is not a
logical term for a particle above the baryon mass, so I will call
these particles "uberons." The D meson is another
fundamental level predicted by my math. We use this equation: [1
+ (8 x 16 x 32 x 64 x 128)/210]
= 32,768. Dividing by 9 and multiplying by .511 gives us 1860.5
MeV. The D meson in experiment is about 1865. The math shows us
that the D meson is a baryon with an added spin above the z-spin.
We can add either a second x or a second y level above the z
level, with one giving us 1860.5 MeV and the other giving us 7442
MeV (see the bottom eta). At 7442 MeV, the numerator is the same,
but the denominator will be 28.
The number of 2's depends on whether the outer spin is "doubling"
the inner x or inner y level. One will be orthogonal twice and
the other will be orthogonal three times, so the denominator must
represent this inner doubling.
Other
mesons and uberons
Several other
mesons and uberons can be explained as multiples of the ones
above. Using the tools I have created in this paper, we can find
the structure of any meson or uberon. For instance, the vector B
meson is just three taus. We can see this immediately from the
energies. The rho meson is one baryon without x-spin and two tau
neutrinos. The strange D meson is four kaons.
The charmed
B meson is the first uberon state (7442 MeV) without inner
x-spin, plus two pions. That gives us 5973 + 140 + 140 = 6253.
The charmed B in experiment is 6275. Once again we have the
baryon and pions missing the same x-spin, from the same sideways
field.
The so-called vector mesons have much shorter lives
than most of the others, and this is because they are often
initial states of pseudoscalar mesons. The vector meson decays
into the pseudoscalar meson on the way down. This does not mean
that the vector mesons are taking part in quark bonding or
anything else. They are not bosons. They are simply more complex
multiples of the basic states shown above, which makes them more
unstable and often larger.
Conclusion
Perhaps
after all this you can see that the ad hoc
quantum numbers of QCD are no longer needed. CP
parity, for instance, is completely explained by stacked
spins. We don't have "vector" mesons or "pseudoscalar"
mesons, we simply have mesons and uberons. Inner spins give us a
simple mechanical and visualizable explanation of parity, as well
as all the other quantum numbers like spin, isospin, and flavor.
My theory will do a housecleaning not only on the particles, but
on the names. We can now jettison most of the useless and
unmechanical vocabulary of atomic physics. In upcoming papers I
will suggest simpified terminology to go with our new simplified
physics.
If this paper was useful to you
in any way, please consider donating a dollar (or more) to the
SAVE THE ARTISTS FOUNDATION. This will allow me to continue
writing these "unpublishable" things. Don't be confused
by paying Melisa Smith--that is just one of my many noms de
plume. If you are a Paypal user, there is no fee; so it might
be worth your while to become one. Otherwise they will rob us 33
cents for each transaction.
|