superposition again by Miles Mathis

SUPERPOSITION AGAIN

by Miles Mathis

First posted April 15, 2009

I recently received a question from a reader, concerning my superposition paper:

I've studied your paper (on superposition) and it made sense to me. However, there are other cases of superposition that are available that do not require measurement of x,y spins of electrons. For example this video at youtube* shows a well-known experiment of superposition using beam-splitters and mirrors. Although I'm personally skeptical of "same particle in multiple places at the same time" argument, I'm struggling to come up with a better explanation. So here is my question: how would you explain this particular superposition experiment? Is it really the same photon in multiple places?

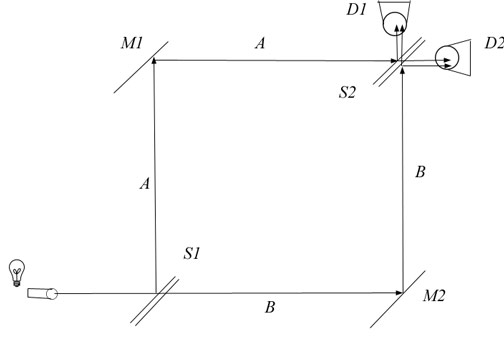
What this reader is talking about is an experiment where a light beam is split, mirrored symmetrically, then split again (see diagram above). Detectors are set up at the second split, and we have another big and spooky “mystery”. The magicians at youtube claim this is because the same photon goes both paths and interferes with itself.

This is a similar question to the one I solved in the first paper, but here the magicians vary the setup to fool the audience. When I say “magicians” I am not just being sardonic. This really is a case of prestidigitation, like a shell game. The fake physicists misdirect your eye, and by the end of it you can't say where the photon is or why it is there. Just as almost no one, no matter how smart they are, can tell what the trick is in a good magic trick, almost no one can sort through all the misdirection and fast talk of the current superposition patter.

First of all, to solve this, we don't have to “measure” spins of electrons or photons. We just have to give the particles wavelengths, and the standard model already does this. The magicians at youtube do this, and they even try to prove double existence by manipulating wavelengths (in a very sloppy manner). But they don't define the wavelengths carefully enough. This forces them to solve the problem by proposing the impossible. It does not bother them to propose the impossible: in fact, they enjoy being magicians. They enjoy performing miracles and dumbfounding the audience.

But let's solve it with mechanics instead. We know that the first beam splitter S1 splits 50/50, since if we move the detectors up to S1, the detectors tell us this directly. The second splitter S2 is exactly like the first, so we should expect the detectors at the end to give us the same 50/50 split (we are told). Instead we find all the photons at D2. Big mystery.

At youtube they explain it in this way. If we fire the photons one at a time, the photon takes both paths and interferes with itself, keeping it from reaching D1. The problem with this answer is not just that the same photon travels both paths, although you would think that would be enough to disqualify the answer. The other problem is that if the single photon has interfered with itself, how does it reach D2? We have a detection at D2, remember? The standard answer is that the interference only happens with the half of the photons that pass straight through the splitter on path B. The half that are split are turned directly into D2.

So, if a photon on path B passes straight through S2, it interferes with itself, and doesn't go to D1. If a photon on path B is turned, it doesn't need to interfere with itself, and it goes to D2. If a photon on path A is going to be turned at S2, it interferes with itself and does not go to D1. If it goes straight through S2, it does not interfere with itself, and goes into D2. That is the magic answer.

Not only is that answer much more complex than it needs to be, it is contradictory. Along path A, the interference takes place on the near side of the splitter. The photon on the A path does not go straight through the splitter: it waits for its twin to go through the splitter on path B, and only then is the interference completed. But if the photon is moving on path B, it goes through the splitter and then interferes with itself. The interference takes place on the A side of the splitter both times. Not only are the paths not symmetrical, there is no way to explain how the photons know whether they are the primary photons or the twins. In other words, the youtube magicians haven't explained why the interference always takes place on the A side of S2. Why doesn't the interference ever take place on the B side of S2, after the photon on path A has passed straight through S2?

Also, you can see that they need the single photon to take both paths every time, just in case it is needed. This is what the sum-over proposition of Feynman means. Every photon takes every possible path, then we do the math at the end, to cancel wavelengths and decide where particles will be detected. But if that is the case, why aren't the twin particles detected when the detectors are at S1? In other words, once they explain the action of the splitter and photons at S2, they have to go back and see if it works at S1. We have the proposal that all photons take both paths. If they are on both paths, why did the detectors at S1 find a 50/50 split? Why do detectors detect primary particles but not twins?

This explanation wants the photon to take both paths in the second case, where the detectors are at S2, but it doesn't want the photon to take both paths when the detectors are at S1. If the photon is on both paths, then both detectors at S1 should detect all the photons. Yes, logically, we should detect 100% more photons than are emitted, since we would be detecting both the particles and their twins.

So the current magical explanation not only wants us to believe that the photon takes both paths, it wants us to believe it is on the path and not on the path. It is on the path when we want it there to interfere with itself, but it is not on the path when we don't need it to interfere. The current explanation is not one miracle, it is two miracles stacked.

The funny part is that the youtube magicians tell you the right answer, but then deflect you from noticing it is sufficient, without interference. They admit that each turning will shift the wave ¼ wavelength. If the wave passes straight through a splitter, it is not shifted. So, in order to reach D1, the wave is either shifted three times on path A, or one time on path B. To reach D2, the wave is shifted 2 times on either path. This tells us immediately that the experiment prefers even shifts. We should then seek to explain this without interference or doubled particles.

The splitter, that we expected to work the same way in both positions, is not working the same way in both positions. At S1, it is letting half the particles pass straight through. At S2, it is letting all the particles on path A pass and none of the particles on path B. Why?

The answer is even simpler than my answer to the detectors-in-sequence problem of my first paper. As in that paper, the first splitter is acting as a polarizer. It is sorting the photons coming from the emitter. All the photons going on path A have the same orientation, and the same for B. They are on the path they are on because they reacted the same to the material in S1. The photons on path A are all equivalent in orientation to eachother, but they are opposite in orientation to the photons on path B.

This means the splitter at S1 is dealing with a different incoming group than the splitter at S2, and we should not expect the splitter to act the same in the two places. The first problem, therefore, is our expectation that they should act the same. The magicians tell us that the logical expectation is that the splitter should act the same in both places, but that is false. It is either a lie or a very big and obvious mistake.

The splitter at S1 is receiving one group of mixed photons, from one direction. The splitter at S2 is receiving two groups of polarized photons, from two directions, and each group is opposite the other group.

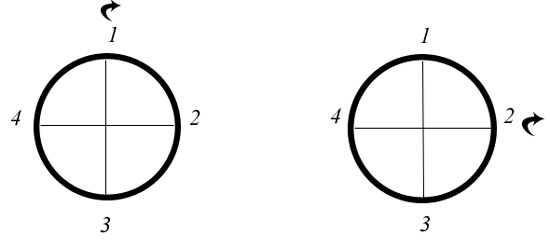
Let us show this in more detail, but still very simply. Let us say photons can either be spinning around a vertical axis or a horizontal axis, relative to the first splitter. In other words, if we simplify the photon into a circle, it is either spinning along a 1-3 axis or a 2-4 axis. All our emitted photons are either 1-3 or 2-4. If they are 2-4, the splitter lets them pass straight through along path B, without deflection. If they are 1-3, the splitter deflects them along path A. But in deflecting them, the splitter turns them ¼ turn, as the magicians on youtube tell us as they read from the internet. This means that the number 2 is leading on both paths. When the particles are turned by the mirrors, they each shift ¼ turn, so that the number 4 is then leading on both paths. The mirrors are opposite in orientation themselves, so we turn the B particle clockwise but the A particle counter-clockwise. But on path A, the particle is still spinning on the 1 axis, and on path B, the particle is still spinning on the 2 axis. So the particles approach the splitter at S2 as shown in the diagram.

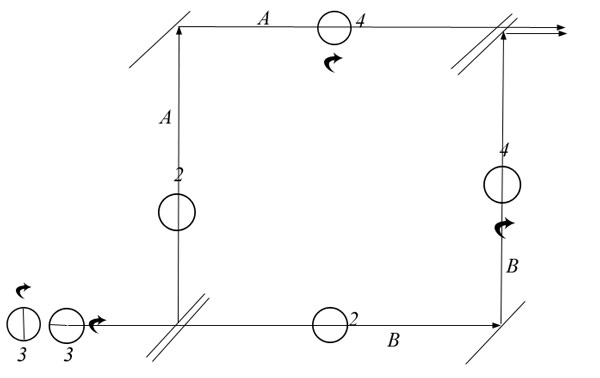
The particles on both paths are now reversed from their original orientations, as you can see. So the splitter reacts to them in the opposite way, turning the B particle and letting the A particle pass.

All the particles on A are the same, so the splitter reads them the same way, letting all of them pass. All the particles on B are the same, so the splitter reads them the same way, turning all of them. Very simple. Not mysterious at all.

Not only is there a mechanical explanation, the explanation is quite quick and transparent, yielding to very simple diagrams. We don't need any interference or doubled particles or multiple paths. The youtube video tells us that the only way to explain loss of detection at D1 is by interference, but I have just shown that is false. The expert on the video also tells you to trust him, but that is very bad advice. Never trust anyone, least of all a scientist. Science is not about trust, it is about a logical and physical explanation.

Of course, this once again destroys the Copenhagen Interpretation and 90 years of physics. Quantum physicists have been assuring us that this couldn't be done. They have assured us that no logical answer could be given, and that no diagrams could be drawn. I have given them and drawn them, as you can see with your own eyes.

Some will complain that my explanation requires spin, whereas the current theory gives the photon a wave, not a spin. My answer is that it doesn't matter one way or the other. I believe the photon is spinning, and have shown theoretical and physical proof of it elsewhere, but my explanation here doesn't require you to believe it. The spin in this explanation simply allows me to show the wave more easily. The standard explanation of superposition comes from Feynman, and it is likely these youtube people are reading something by Feynman off the internet as they make their film. Well, Feynman also invented a thing called the shrink-and-turn method, which I pull apart in another paper. To illustrate the wave, Feynman uses little clocks, much like I have here. That is, he draws a circle with numbers on it and lets that stand for the wave as the photon travels. He doesn't call it a wave, true, but it works just like my wave here. His method works precisely because it mirrors my mechanics here. Well, take the little circles above as waves if you like, rather than spins. Spins create waves in a direct manner, so they are great for illustrating waves even if you don't like spins. If you don't want to assign the waves to spins, fine with me. Assign them to wobbles or leaps or hiccups or to nothing. I don't care. The point is, I solved the problem with diagrams, mechanically, without interference, without ghost particles, without multiple paths, without spooky forces, and without mystification or magic.

And finally, as a bonus, I give you the fact that the current explanation of superposition, using light interfering with itself, contradicts the current explanation of the Sagnac Effect. Wikipedia admits that the Sagnac interference math is the same both before and after Relativity. Classical physics made the same predictions as post-classical physics, regarding this effect. And, since the Sagnac Effect already had a satisfactory explanation and math before quantum physics, it didn't require the sort of explanations that have been devised for superposition. This despite the fact that the two experiments have much in common, as you see, using mirrors and beam splitters (a half-silvered mirror is a sort of splitter) and square circuits. The reason this contradicts the Sagnac Effect is that, to be consistent, we have to take the quantum explanation into that experiment as well. We can't have light interfering with itself in some cases and not interfering with itself in other similar cases, just to suit sloppy theorists. If light takes all possible paths, why doesn't it do so in the Sagnac experiment? If we let light take both paths in the Sagnac experiment, we immediately ruin our math and our explanation. Instead of getting light where we need it, we get light where we don't need it. We have too much light on both paths, and the result is either a total cancellation or a big mess. This is the problem with so many of the current jerry-rigged theories: they are very problem specific, and the magicians just hope you don't try to universalize them, and apply them to similar problems. Because if you do, you find out that they are completely ad hoc, and therefore physically false.

To read more on this, you may go to my paper on entanglement, where I analyze and solve the problem, using a hint from Feynman and my quantum spin equations.

More recently, I have blown apart the CHSH Bell tests, unveiling the terrible mathematical cheat at the heart of these experiments. This leaves entanglement in tatters.

Addendum, July 2011: I was asked by a reader why I didn't set up some experiments to prove my theory here, and my answer was that it is unnecessary. The experiments have all been done already, they just haven't been interpreted correctly. As a further example, we have what is called a quantum eraser, by which interference patterns can be "added back" into an experiment that has "lost" them. This is done by a further polarization or turning of the photons by 45^o. But of course anyone who has understood my argument here will realize that the quantum eraser is more obvious proof of my mechanics. Once we give the photons real spins, we can explain all these experiments without that much effort. To see what I mean, you may want to watch this other video at youtube, where the speaker Ron Garret talks of polarizing individual photons, of up and down photons, and so on. Of course this begs a very big question he never answers or even addresses: How can photons that are point particles in the gauge math, with no extension and no mass, be differentiated? What is up about them, or down about them? How is the polarizer sorting them, especially when they are traveling one by one? In this way, we are reminded that polarization itself is a proof of my mechanics. A point particle cannot be polarized.

I will be told that it is the wave that is polarized, not the particle, but that is just dodging the begged question one more time. Neither the old quantum mechanics nor any of the updates ever bother to tell us how point particles with no radius can create waves, or move in a wave motion. My mechanics explains it, but my mechanics requires a photon with a radius, and with several stacked spins. Without them, mainstream physicists can only rush by this basic question. I have already told you why they do this in about a hundred papers: they are hiding behind the math. If they bring the mechanics back to the front, and let you see all these existing questions in a full light, their famous math begins to melt. Ron Garret calls the squared amplitude in the wave equation a hack, but all the math is hacked from top to bottom, as I have shown.

Again, the thing to take from this addendum is that polarization and superposition are both proof of real photon spin. To create quantum erasers and things like that, each individual photon must have a wavelength. I repeat, not just the wave front, or the wave packet, but each individual photon. This must mean that the polarizers are working upon individual photons, not on wave fronts or fields of photons. And for that to be possible, each photon must have a radius. A photon with no mass and no radius is undifferentiable. In other words, there is no way for a polarizer or other detector or filter to know one photon from another. You cannot tell one point from another. And this means that photons must have mass and radius. And this means that the math of QED, as we know it, comes tumbling down. Ron Garret thinks he deserves a Nobel Prize for noticing that entanglement is a measurement, but he fails to notice that QED needs more than a tweak. It needs a complete overhaul, from the baseboards up. We have to throw out all the math and all the theory and start over from the beginning.

For more on this question, you may now read my paper on Polarizers in Sequence.

*http://www.youtube.com/watch?v=qpQABLRCU_0

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.