return to homepage
return to updates

Three Problems Solved Mechanically:
PARTIAL REFLECTION BY GLASS
THE RIGHT-HAND RULE
AND FEYNMAN'S

SHRINK-AND-TURN METHOD

by Miles Mathis
milesmathis.com

A smith is put to shame,

And learns from the lad he taught;

All the master's lore is useless now.

—Wagner, Siegfried

Abstract: In this paper I will show why Richard Feynman’s “shrink-and-turn” method works. In doing so, I will be able to show a mechanical cause of partial reflection by glass, one that is different from that of Feynman, Newton, Huygens, or anyone else in history. Finally, I will show how the right-hand rule of E/M is caused by the simple motions of photons.

The subject for this paper occurred to me while I was re-reading my recent paper on QCD. There, I mention in a footnote that I followed the emitted photon out through the four spins of the baryon by using a toy dog. I would sit in a chair, holding my plush friend up in front of me, and like Einstein riding his lightray, would imagine the two of us actually making the trip out through the spins. At each intersection of spins, I would turn the dog 90^o to the left or right, and also spin him 90^o. In this way I could compare his final position to his initial position, and find in that way both the correct vector and the correct spin orientation at emission from the z-spin. In re-reading this drole footnote, I realized that my method had somewhat in common with Feynman’s “shrink-and-turn” method with arrows and clocks, which he used to find amplitudes or probabilities. Feynman always considered this method just a trick, and in his book QED he calls it “absolutely ridiculous.”¹ But in my second paper on Feynman, I critique this book, and there I mention that Feynman’s method seemed to me to be very suggestive, a pointer to some real mechanics. I even stated that it was so suggestive that I suspected a cover up. I suspected (and still suspect) that Feynman knew his method implied a particular mechanics, and I suspected that contemporary physicists were resisting Feynman’s method precisely because it had a mechanical flavor to it. Back in the 70’s and 80’s, this shrink-and turn-method was often taught to graduate students, especially on the West Coast, but you don’t hear much about it anymore. In fact, a web search leaves you pretty much empty handed. I take this to mean that the current masters of QED prefer to keep the theory under the heavy mathematical blankets, rather than allow the theory to be taught in visual or faux-mechanical terms. The last thing these physicists want is a rigorous mechanical analysis of QED, since that would bring all their gigantic holes into view.

At any rate, I soon saw that I now had a physical explanation for what I only suspected a few years ago. I now had a way to show exactly why Feynman’s method worked, from a fundamental, kinematic perspective. The “turn” part of the “shrink-and-turn” method was coming right out of my stacked spins.

Before I clarify that connection, though, I want to take a look at the right-hand rule. Both Feynman’s method with the arrows and clocks and my method with the toy dog are connected to the right-hand rule. Once I point it out, this connection is not hard to see, and others may have made the connection before me between Feynman’s turning and the right-hand rule. But until now, no one has been able to say exactly what that connection is.

The right-hand rule is just a rule of thumb for finding the direction of the magnetic field given the electric field (or vice versa). Using your right hand, you curl your four fingers and point your thumb straight up. If you match the direction of your thumb to the direction of the electric current, then your fingers will tell you the direction of the magnetic field. This has been known for a long time, but it has never been explained mechanically using quantum relationships. In other words, until now the right-hand rule has been heuristic or experimental knowledge, not physical knowledge of the field. Up till now, no one could tell you why we don’t have a left-hand rule instead. It is a loss of parity in the field that has been pretty much left in the dark.

The reason we have a right-hand rule is that the charge field is right-handed itself. This is new information, coming out of my field analysis: it is unknown to the standard model and was unknown to classical E/M theory. For pre-quantum electrical theory, the charge field was simply a field of potentials. Neither wave mechanics nor spin had any place in the theory. Faraday’s field was a field of lines, and so was Maxwell’s. The charge field of QM and QED was also not given spin, chirality, or any other non-symmetry. All the spins of QM are given to the electron. To give the charge field spin would have required giving the virtual photon spin or some other heterogeneity, but the standard model has never reached that level of cleverness, even to this day. Quantum Mechanics gave up on mechanics 80 years ago, and any new necessary “degrees of freedom” were given to the math, not to the particles.

But in my field, the charge itself has charge. The first charge is the emission of the photons. Charge energy is transferred by the linear motion of these photons. The second charge is the spin of these photons, since it can either be CW or CCW. The charge field can either be plus or minus, since it creates potentials; but the spin of the field can also be plus or minus, in a way, since we can always assign a plus to CW and a minus to CCW. So the electron actually needs two signs on it, not just one. It needs the first minus sign to signify that it is at a lower potential regarding charge, being on the receiving end of the charge field in all relations with the proton or nucleus. And it needs a second sign to differentiate it from the positron. This sign tells us the spin direction of the emitted photons.

Now, the standard model knows this, in a way. It knows that the positron and electron are opposites in some way, and it often uses a charge sign to designate this difference. But it cannot say what the charge sign applies to, mechanically or physically. It has certainly never assigned this difference to the spin of the photons emitted. It could hardly do so, since the charge photons of the standard model are virtual. Beyond that, they are point particles with no size and no mass. They could hardly spin without size and radius.

The reason the charge field is right-handed is strictly a local phenomenon, decided by a confluence of natural factors beyond the reach of this paper. The charge field can be either right-handed or left-handed or neutral, but on the Earth it happens to be right-handed. Why? Because on the Earth, in almost all cases, the charge field is emitted by matter rather than by anti-matter.

The entire and defining difference between matter and anti-matter is that matter emits a right-handed charge field and anti-matter emits a left-handed charge field. To say it even more clearly, matter emits photons upside-up, and anti-matter emits photons upside-down. Emitted photons are always spinning, so anti-matter emits photons that are spinning “the wrong way.”

Now, the Earth contains both matter and anti-matter, but it contains a preponderance of matter. Contrary to popular opinion, matter and anti-matter do not annihilate one another when they meet. No, their charge fields cancel each other, and the particles therefore have no cushion or protection. They collide, and in collision their outer spins cancel. In this way they loose a large portion of their energy and therefore of their mass. But they do not dissipate into nothing. They dissipate into small non-spinning particles, which, due to this lack of spin, become invisible to detectors. But, given time, they can, through more collisions, develop new spins and new higher energies.

What explains the preponderance of matter over anti-matter in our region is that anti-matter that has been stripped of spin in this way will reform as matter. Say you start with an anti-proton. It collides with a proton and loses all four spins. At this point it is like a non-spinning electron. What is a non-spinning electron? I have shown that a non-spinning electron is nine times smaller than an electron at rest with axial spin, which is what we call an electron. A non-spinning electron is also invisible to normal detection, since ionization detectors and other detectors cannot detect non-spinning quanta. They have no velocity relative to the field and make no tracks.

But very soon these quanta are bumped by other quanta, and they gain both velocity and spin in this way. In most cases, they are bumped by photons, since photons make up the charge field. Photons outnumber everything else by a very large margin, so the odds are very good that this non-spinning electron will gain its new energy from photons. But most of these photons are right-handed photons, so the particle will rebuild as a proton. It gets its spin from the field, and if the field is right-handed, the particle’s new spin will also be right-handed. This means that a normal charge field, as we know it, will turn anti-matter into matter, through this simple process. Over time, all local anti-matter will be turned into matter, and the entire local field and everything in it will become right-handed. Only the fact that the macro-field is not homogeneous, rectilinear, and unidirectional keeps the field from being completely right-handed. Because the field of the Earth is spherical, and receives emission from all directions, it maintains a fraction of anti-matter. It also receives anti-matter via the Solar Wind.

You would think this would be the default case in most situations, but it isn’t. Even in our Solar System, it isn’t the default case. One would think that a balance would be hard to maintain, and once the balance was lost the field would quickly become either left or right handed. But the planets nearest to us, Mars and Venus, appear as proof against this assumption. Both planets are nearly non-magnetic, and I have interpreted this to mean that their overall charge fields are neutral. They lack a magnetic field because their charge field is neither right-handed nor left-handed, and this is due to equal charge emission by matter and anti-matter. The planetary system as a whole on Mars and Venus has not lost its charge symmetry, and therefore the anti-matter has not been turned into matter. I don’t yet have a firm theory for why this is, though it might be that life is a catalyst for loss of charge symmetry. Life on Earth causes an increase in all interactions and events, and this increase may increase overall ionization and collision, which increases the likelihood of imbalance in the charge field. A charge field that mediates fewer events, as on Venus or Mars, may find it easier to maintain symmetry. A symmetric field, in this case, is a non-magnetic field.

By this analysis, it is likely the universe, the galaxy, and perhaps even the Solar System, has many planets where the left-hand rule is correct. There is nothing intrinsically strange about anti-matter, and we could not easily tell the difference between a world made of matter and one made of anti-matter. The only difference would be in rules like the right-hand rule.

As I have shown with my stacked spins, you can build either a proton or an anti-proton from an electron. You do not need to make anti-matter from anti-matter or matter from matter. They are not fundamentally different. Just as you can turn a neutron into a proton, simply by reversing the z-spin, you can turn a proton into an anti-proton simply by reversing the y-spin. You can’t do this just by applying a field to a proton, since you can’t reverse inner spins without affecting outer spins; but you can do it by building the anti-proton from an electron or meson. You simply have to hit it with the right fields in the right order. But my point is, you do not have to build an anti-proton from a positron. So there is no fundamental difference between matter and anti-matter. Anti-matter is not freakish or foreign, it is just emitting photons upside-down compared to “normal” photons, and it is emitting them this way only because of the way its spins stack up.

From this we can see that the non-mechanical nature of both QED and QCD have kept them from answering questions like this. I have argued in many places that the mathematical complexity of QED and QCD and their lack of a physical foundation have made them impervious to understanding, correction, and almost all critique, but the most critical failing of both is their lack of explanatory power. A successful mechanics, once understood, can be exported into other fields and other problems. A clearly stated solution leads to a line of solutions, since one can easily see how to move from problem to problem. But with dense modern theories, connections like this are difficult to make. Nothing is ever a clear pointer to any other problem or solution, so that physics gets bogged down in minutiae and esoterica. Instead of striding boldly from one success to the next, the field becomes stale and academic, and has to be defended from all rigorous analysis and outside influence.

My explanation of the right-hand rule is neither esoteric nor especially creative: it is simply putting together a series of logical steps. In fact, it is much less “inventive” than most things that pass for theoretical these days. But this explanation was made possible by my initial explanation of superposition, in which I first discovered stacked spins. And that explanation was made possible by my insistence that quantum interactions could be and must be explained sensibly and mechanically, with all classical rigor.

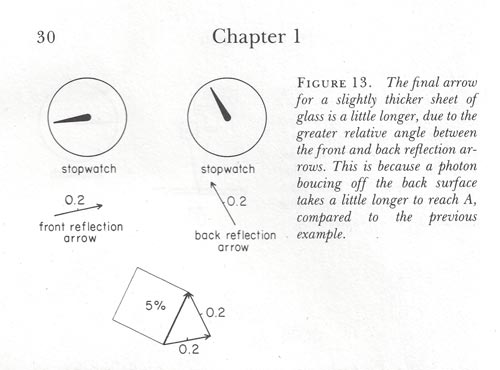
Now let us return to Feynman. Feynman begins his shrink-and-turn analysis in the book QED by analyzing partial reflection by glass. He tells us that it has long been a great mystery: that Newton couldn’t solve it, that Huygens couldn’t solve it, and that wave theory couldn’t solve it. Newton couldn’t solve it, he says, because, despite the fact that Newton correctly chose the corpuscle or particle theory of light, Newton couldn’t explain how the light knew how many reflective surfaces an object had. Wave theory couldn’t solve it because classical waves would be expected to diminish with dimmer light. But the detectors do not detect a diminution with dimmer light. Dim reflected light “clicks” less often, but just as “loud,” and Feynman takes this as proof that light is not a wave.

Feynman admits that QED also has no mechanical explanation for partial reflection by glass, but it is superior, he tells us, because it can supply a very precise math. Of course, Newton also supplied a successful math, but because Newton tried and failed to explain it mechanically, and because QED gives up on attempting an explanation, QED is supposed to be superior. We must suppose that Feynman believes it is better to have never loved at all, rather than to have loved and lost. It is better to refuse to explain a phenomenon, rather than try to explain it and fail.

At any rate, with partial reflection, experiment shows that it is the thickness of the glass that is important. Given a type of glass with an overall reflective index of .04, the real reflection will vary from 0 to .16. Yes, very thick pieces of glass, of just the right thickness, will allow all the light to pass without reflection. And thinner pieces, of just the right thickness, will square the reflection. Other thicknesses give values between these maxima and minima.

The crucial part of Feynman’s method is that he assigns a vector or arrow to each photon. The length of the vector is pre-determined by the reflective index, but the direction of the vector is determined by the how far the photon travels before being detected. Feynman uses a dial clock to measure this distance, letting the second hand move as the photon moves. He lets the photon reflect from both the front surface and the back surface of the glass, and then does a vector addition of the two draws. The angle difference between the two vectors becomes his final amplitude or probability.

Feynman spends a lot of time in this book telling us light is a particle and not a wave, but the turning dial on his clock is acting just like a wave function here, as is clear to anyone awake. And not just like a wave function, but like a physical wave. A turning clock IS a wave, since the numbers come in waves. The number 12 comes with a definite period, of wavelength twelve and frequency 1/12. Feynman’s method works only because his clock is a wave.

But why does this method work? We will suppose that Feynman didn’t know, although, as I have said, it is very possible the masters of QED have known all along that a fairly simple mechanics underlies these interactions. They may have suppressed the mechanics for two reasons: one, the arcane sells better than the simple, and is easier to control; two, the simple explanation could not be made to work with the old electrical field, which QED has kept hidden underneath its mathematical blankets. If we admit that the photon has spin, we have to admit that it has radius, which means it has mass, which means it is not virtual, which means the charge field has mass, which means energy is not conserved in emission, which means that QED has to be rebuilt from the ground up. No one wanted to do that, so it was better to pretend that QED was a big mystery, unlocked only by magicians with blackboards full of math.

Feynman wants you to believe that this problem of partial reflection is very great, as I have already shown—to the point, in fact, that it is physically insoluble. He wants to add it to the list of things you don’t need to try to solve, since Newton couldn’t solve it and neither can he. He stops just short of adding it to the Copenhagen list of things you are forbidden to look at, since they are impossible to solve.

Despite this, I think we can say that Feynman makes some astonishing assumptions. Feynman shows that Newton dismissed the idea that reflection took place at the first surface, because, “how could light reflected from the first surface be captured again when the thickness is such that there was supposed to be no reflection at all?”² This is obviously a good point, but Feynman runs past it without analysis, dismissing Newton’s analysis in toto because Newton then proposes “fits of easy reflection or easy transmission.” Yes, Newton’s idea of these unexplained “fits” is not a good one, but the idea of “fits” is separate from the idea of non-transmission from the first surface.

I bring this up because, as I have shown, Feynman lets his photons reflect only from surfaces. But he does not give any reason for doing so. Why should reflection take place only at surfaces? How can Newton be wrong in his deduction that reflection cannot take place from the first surface? In fact, Newton cannot be wrong about this. Feynman’s method of using front and back surfaces can work only by averaging, as I will now show.

Since molecules exist throughout the glass, and since the light must be interacting either with these molecules or with their E/M field, we must assume that reflection occurs throughout the material, not just at the surfaces. Something special may be occurring at the surfaces, but the main effect must be taking place within the material.

Rather than treat photons as point particles, we will treat them as particles with spin. This spin will immediately provide us with a wavelength, and we will see if that wavelength can explain partial reflection. Feynman tells us that wave theory cannot explain the way our detector works, but that is only in the case that light is a field wave, like sound. If light is a particle with spin, then the wave belongs to the particle itself, and will not diminish with dimming light. In this case, each photon has a wave, and this solves the first big mystery all by itself. The wavelength does not belong to the wavefront or to a large group of photons; it belongs to each photon individually. In this way, the wave can be carried full strength to the detector, even with only one photon.

From this point on, my solution is just a restatement or variation of the wave solution Feynman dismissed. Up to the 19^th century, there existed a wave solution to this problem, as Feynman admits. Since I have already shown that his critique of the wave solution no longer applies, I have already proved my point, and we can resuscitate the wave solution. Feynman says the wave solution can’t be right because wave theory predicts wave diminution. But his critique doesn’t apply to my waves as spins, since the wave is now carried by each particle. My spin theory fills in the holes left by classical wave theory, and the mechanics is fully explained. In this way, Newton, Huygens, and Feynman are all partially correct, and so is Bohr. Light is both a particle and a wave. It has a duality, if you like, although that duality is no longer squishy or undefined. Light is a spinning particle, and the spin creates the wave in a simple mechanical fashion. The wavelength is simply the spin radius. This spin radius is then stretched by the linear velocity of the photon, as I have shown elsewhere in detail.

What does this have to do with Feynman’s clocks? Feynman’s clocks follow the motion of this wave as the photon travels through the glass, telling us where the photon proper is in its spin wave at each dt. Like the electron, the photon must have at least two spins to show a wave and to explain these physical effects. It must have an axial spin and an x-spin, with the x-spin twice the radius of the axial spin. Feynman’s clock measures one spin against the other, and tells us where the body of the photon is in the greater x-spin. The body of the photon cannot inhabit all the space in the x-spin, obviously, since the photon has a radius of 1, say, and the x-spin has a radius of 2. Since reflection is a collision, we need to know where the body of the photon is in the wave. We then combine that information with the molecular structure of the glass, to determine how much space is in the glass, how likely a collision is, and what the deflection or reflection angle must be. Feynman’s clock tells us the first of these variables: where the photon is in its own wave. The length of his vector or arrow is taken from the known index of the glass, and that is second variable here: the molecular structure of the glass. This molecular structure, being structure, then acts as another wave. A sort of standing wave.

It is a standing wave not in any esoteric sense, but only in the sense that any patterned structure is a wave. A cattle guard is a standing wave, in this sense, because its structure is a definite and fixed pattern, one that we can mathematically treat like a wave. Since we have one wave meeting a second wave, we can use pretty basic wave mechanics to predict collisions.

After that, Feynman’s use of front and back surfaces actually has nothing to do with surfaces. It has only to do with limiting the math. Feynman’s method does not happen at these surfaces, it happens between these surfaces. His waves interact between these surfaces, so that he is actually averaging from front to back. Or, to say it another way, he is summing over that width, from front to back. His integral is taken from front to back. If your integral goes from 0 to 1, that does not mean that things are happening only at 0 and at 1, it means that things are happening between 0 and 1.

¹QED,, p. 24.
²QED, p. 23 footnote.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.