return to homepage
return to updates

The Trouble
with Tides

by Miles Mathis

First posted October 7, 2005

Tidal theory is one of the biggest messes in contemporary physics. I will start with tides on the Earth, since they have gotten the most attention and the most theory. We know the ocean tides are caused by the Moon, since they follow lunar cycles. But are they caused by the Moon’s gravity? Let’s look at some numbers. Let’s compare the Sun’s field to the Moon’s field, at the Earth.

a_S = force on the Earth by the Sun
a_M = force on the Earth by the Moon
a_S = GM_S/r²
      = .006 m/s²
a_M = GM_M/r²
      = .000033 m/s²

You can see that the Sun has a much stronger gravitational effect on the Earth, if we look strictly at field strength. We could have guessed this without the math, since if the Moon had a stronger gravitational effect, we would be orbiting it, not the Sun. If tides are caused by gravity, then it seems like we should be experiencing Sun tides that utterly swamped our Moon tides. By the math above, Sun tides would be about 180 times as great as Moon tides, making the Moon tides invisible. They would follow the movements of the Sun overhead.
      Why aren’t we experiencing Sun tides that are stronger than Moon tides? According to an article at Wikipedia, which is following the Standard Model and which is reprinted all over the web,

Gravitational forces follow the inverse square law (force is inversely proportional to the square of the distance), but tidal forces are inversely proportional to the cube of the distance. The Sun's gravitational pull on Earth is 179 times bigger than the Moon's, but because of its much greater distance, the Sun's tidal effect is smaller than the Moon's (about 46% as strong).

F_S = GmM_S/r³
      = 2.4 x 10¹¹ N
F_M = GmM_M/r³
      = 5.1 x 10¹¹ N

These equations, as I have simplified them here, don’t give the right numbers, but we do get 46%. How was this "inverse cube law" derived? According to a University of Washington website¹,

Tidal forces result from imperfect cancellation of centrifugal and gravitational forces a distance L away from the center of gravity of the system and have the form F_t = GmML/R³

Other websites agree. Here is one that is especially funny, considering everything:

So the gravitational attraction of the Sun is 178 times greater than that of the gravitational attraction of the Moon. But how can this be? We all know the moon is more effective in producing tides than the Sun. There is a simple explanation for this, and it is not that we have been lied to! It is only the proportion of the gravitational force not balanced by centripetal acceleration in the Earth’s orbital motion that produces the tides.²

Two major problems here. One, the gravitational force causes the centripetal acceleration. There can be no lack of balance. As for the gravitational and centrifugal forces, although they are caused separately, they cannot cancel, since they both tend to create tides. In fact, most physics books and websites use a summation of centrifugal effects and gravitational effects to create tides on the Moon, as I will show below, since both are tidally positive. That is to say, gravity would create tides even without circular motion, and circular motion would create tides even without gravity. So the two are additive. There is no possible cancellation, in the way that is assumed above. Besides, the Earth is not feeling a centrifugal effect from the Moon, since the Earth is not orbiting the Moon. Even if it were orbiting a barycenter, it still would not be in circular motion about the Moon. Therefore the tides on the Earth could not be an imperfect cancellation of centrifugal forces and gravitational forces, even if these forces were in opposition. There are no centrifugal forces on the Earth directly caused by the Moon, since there is no angular velocity around the Moon.
      Secondly, the math above is dishonest. If we look at the Sun/Earth system, then the center of gravity of the two bodies is so close to the center of the Sun that it makes no difference. The Earth has almost no effect on the Sun. Therefore, the distance L is just the radius R, and the equation is the same as

F_t = GmMR/R³

That is not an inverse cube law, it is an inverse square law in poor disguise. But the author seems to realize that, so he continues to add layers of heavy clothing. He continues:

However, for a spherical object with an average density d and a radius r we can view its mass as the product of its density and volume, so that M = d (4/3πr³). Then the tidal force has the form
F_t = (π/6)GmLd(2r/R)³, so that F_t ~ d (2r/R)³

Beautiful. You don’t see magic like that everyday. The trick here is in losing the L variable. The author needed to get rid of that so that he would not have to cancel it with his R³ in the denominator, bringing it back down to R². So he surrounded it by as many variables as he could. This confuses the reader, who he then hopes will miss the flaw in his quick claim that F_t ~ d (2r/R)³.
      But that last equation is flat wrong. It does not follow from the previous equation, since if you are computing proportionalities, you cannot create a proportionality to distance, and then leave one of the straight distance variables hanging. The last equation is a proportionality between force, density and radius. But L is part of the radius. It cannot be separated out like that and then left behind. I have shown that with the Sun/Earth, L is almost the same as R. Even with the Moon/Earth, L is very close to R. You cannot mathematically just ditch it like that.
      You can see this more clearly if you go back to the equation F_t = (π/6)GmLd (2r/R)³. Remember how he got there. If that equation is applied to the Sun, then L = R and the equation reduces back to F_t = GmM/R². It therefore can’t differ from the force that is 180 times the Moon’s force. It is true that according to the equation F_t = (π/6)GmLd (2r/R)³, the Moon should have a slightly different force on the Earth than the one above. If we take the barycenter of the Earth/Moon to be 4671 km from the center of the Earth, and take R = 384467, then L = 379,740 km
F_t = (π/6)GmLd (2r/R)³ = 1.9 x 10²⁰ N
      All of the fancy clothing didn’t change much of anything. All we did was incorporate the center of gravity of the Earth/Moon, and that did not give us an inverse cube law or lower the force from the Sun. In fact, it only made the problem worse. The Sun tides are now 190 times those of the Moon, instead of 180.
      This has not kept large parts of mainstream physics from accepting the idea that tidal forces are dependent on density or angular size in the sky, and that this density dependence can be given to gravity. The data tells us that the Sun’s force is 46% of the Moon’s, someone throws together a dishonest equation to prove it, and it becomes dogma.

A much better explanation of the inverse cube law is supplied by Wikipedia:

Linearizing Newton’s law of gravitation around the center of the reference body yields an approximate inverse cube law. Along the axis through the centers of the two bodies, this takes the form F_t = 2GmMr/R³

"Linearizing" means differentiating the equation with respect to R, so that this new equation represents a change in the field, rather than the strength of the field. Despite being weaker, the field of the Moon changes more quickly. This causes a greater difference from center to far or near edge. Another way to express this without differentiation is:
a = GM[1/R² – 1/(R-r)²]
      Where R is the distance between objects, and r is the radius of the gravitating object. They tell us this equation is approximately equal to a = GM2r/R³
      Giving us an inverse cube law.

It is clear that the differentiating proves that there would be an inverse cube effect in the tide-producing differentials, supposing that the postulates of this theory are true. I don't know that I would call it an inverse cube "law", since it does not apply to the field itself. It applies to the differential field. It comes from the fact that tides in a static gravitational field are determined by the rate of change of the field, not by the strength of the field. What I mean by static is that this calculation does not take into account the circular motion of the object in the field. Even objects in straight freefall would be subject to this tidal inverse cube law, as Wikipedia and current theory admits. But the Earth is not in simple freefall around the Sun. It is in orbit. We must therefore add a centrifugal effect to the static effect of the field. Once again it appears that this must take the Sun’s effect beyond the Moon’s effect on the Earth.
    To find out, let us actually calculate a force. We know that the centrifugal force varies in a different way from the centripetal force. The centripetal force gets weaker as you go out, since it must be assigned to the gravitational field. But the centrifugal force, in this case, increases at greater radii. This is because the far side of the Earth in its orbit must have a greater orbital velocity than the near side. To calculate this force we must first find the acceleration of different parts of the Earth using the equation a = v²/R.
R = 1.4959787 x 10¹¹ m
v = 2πR/t
t = 365.257d = 31558205s
v = 29784.68322 m/s
R + r = 1.4960424 x 1011 m
R – r = 1.4959149 x 1011 m
v_o = outer velocity = 29785.95147 m/s
v_i = inner velocity = 29783.41297 m/s
a = .00593008 m/s²
a_o = .005930332 m/s²
a_i = .005929827 m/s²
Δa = 2.53 x 10^-7 m/s²
So let’s show the basic equation for the math above:
Δa = [v²/R] – [v_i²/(R – r)]
      = [4π²R/t²] – 4π²(R-r)/t²
      = ω²R – ω²(R – r)      where ω is the angular velocity (= 2π/t)
Δa = ω²r

All that work to get the same number we found at first, way above [.006]. I wanted to show you that the circular motion equation generated the same number as the gravitational equation. This is no accident, of course. Measured from the center of the Earth, the two numbers would be expected to be the same, since it is the acceleration due to gravity that keeps the Earth in orbit, according to gravitational theory. The math above just mirrors the math of the differentiated equations. It is the same in form, but not in output, since the centrifugal field varies differently than the gravitational field, as I have said. Here is the equation for the static gravitational field of the Sun at the Earth:
Δa = GM[1/R² – 1/(R-r)²] = 5.08 x 10^-7 m/s²
      Doing the same math for the gravitational field of the Moon at the Earth, we find
Δa = 1.14 x 10^-6 m/s²
      These two equations yielded the number 46%, remember. But now we have some more tidal effect to add from the Sun. The total tidal effect from the Sun is now
Δa = 2.53 + 5.08 = 7.61 x 10^-7 m/s²
      This does not take us over the effect from the Moon, but it takes our number for Sun tides up to 67% of Moon tides.

The Standard Model, as expressed in Wikipedia and elsewhere, adds the centrifugal effect using this equation:
Δa = ω²mr
      ω is the angular velocity, so, according to Kepler’s law, ω² = GM/R³. This makes the equation equivalent to the math I used. This term ω²mr gives us half of the value of the first term, 2GMmr/R³. In other words, the tidal effect caused by circular motion is half the tidal effect caused by the static gravitational field. On this much we agree, as you can see from my numbers for the Sun [2.53, 5.08]. But the Standard Model goes on to apply the full equation to the tidal effect on the Earth from the Moon:
Δa = ω²mr + 2GMmr/R³
      This equation is equivalent to my math above:
Δa = ω²r + GM[1/R² – 1/(R-r)²]
      But neither equation is applicable, since the Earth is not orbiting the Moon. The first term on the right side cannot be applied, because if you re-expand it, you find that it contains the variable R. Like this, remember:

a = ω²R – ω²(R – r)

This R applies to the Earth-Moon radius. But if the Earth is actually orbiting the barycenter, then this radius R does not apply in the first term of the equation. We must use the number 4,671 there, not 384,400. To get the correct angular velocity, we must use the correct radius. The current equations use 384,400 for R, but the value should be 4,671. That throws off all the numbers, and prevents them from getting the 46% they desire. If we correct the math, we find 67%, as I showed above. But that doesn't match data.

I have had readers answer: "But we are subtracting the R out of the equation, so it doesn't matter what it is." It matters because the value of v and ω are chosen to match that radius. The Earth wouldn't have the same angular momentum around a barycenter that it would have around the Moon, would it? The current equations use a value for ω that implies the Earth is orbiting the Moon; when, at best, the Earth is only orbiting a barycenter.

This means that all the standard model math fails. The mainstream has been publishing false equations. I assume they know they are doing this, since the holes in the equations are so big. Using the wrong radius is a huge error, one that is difficult to explain away as an oversight. It would have to be an oversight of many decades, involving thousands of specialists. I believe it is a purposeful fudge.

[Note added August 2007: Confronted with parts of this paper in late 2005, Wikipedia deleted all its tidal theory math, its tidal theory page, and ordered a rewrite with lots of new illustrations. It appears they are perfecting their propanganda rather than admitting that their math and theory doesn't work. This change affected many other websites as well, since Wiki is linked to a large percentage of online encyclopedic entries. Large parts of tidal theory have gone into hiding since the publication of this paper. One place that is still hanging the dirty laundry out in the open is the department of Oceanography at Texas A&M (ocean.tamu.edu), as I was informed by a reader. All the tidal math there falls to this critique, since it is equivalent to the math that was up at Wiki. It is a pretty variant, but it includes the inverse cube law above, and uses the wrong radius. It is very clever at hiding all the problems, since it hides some variables and refuses to define or assign others. It also hides the barycenter problem, revealed just below.]

Another major problem with tidal theory concerns its use and misuse of the barycenter. The barycenter is the center of gravity of the Earth/Moon system, which both bodies are said to orbit. Feynman was one of the most famous to suggest that the Earth has a non-negligible tide created by orbiting this barycenter. Is this true? Let's do the full math.

R = 4671 km
v = 2πR/t
t = 27.32d = 2360448s
v = 12.43 m/s
R + r = 11042 km
R – r = -1707 m
v_o = outer velocity = 29.39 m/s
v_i = inner velocity = -4.54 m/s
a = 3.31 x 10^-5 m/s²
a_o = 7.82 x 10^-5 m/s²
a_i = -1.2 x 10^-5 m/s²

Δa_o = 4.51 x 10^-5 m/s²

Δa_i = 4.51 x 10^-5 m/s²

We certainly do find a significant effect from the Earth orbiting its own barycenter. In fact, it swamps all other effects. It is 40 times as great as the gravitational effect from the Moon and almost 60 times the total effects from the Sun. However, Feynman was wrong in one very important way. The effect doesn’t just raise a tide on the far side of the Earth from the Moon; it raises an equal tide toward the Moon. Feynman obviously didn’t know what to do with that negative radius. But as you can see from my diagram, it produces a positive tide. You must follow the steps of the math I did previously, and if you do it exactly, you find that you must subtract a_i from a, to achieve the proper differential. As vectors, they are pointing in opposite directions, so you subtract a negative, which is the same as addition.
Δa_i = a – a_i



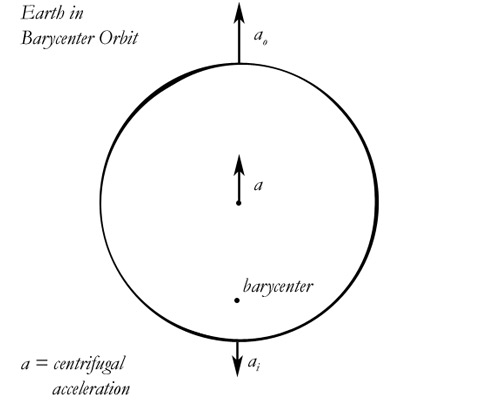
The barycenter falsifies the entire standard analysis, since it would swamp all effects from the Sun and Moon. You cannot include effects from the barycenter, since they cannot be made to fit the given data. And you cannot fail to include effects from the barycenter, since current gravity theory demands a barycenter. This is called a failed theory.

Some have tried to squirm out of this by telling me that since the barycenter numbers are equal forward and back, the tide is a constant and the other tides can just be stacked on top of it. But this is illogical. The numbers show the barycenter tides equal front and back: they do NOT show an equal tide all the way around. The barycenter is a discrete point, and there is a vector pointing from the center of the Earth to the barycenter. This gives the barycenter tide position and direction on the surface of the Earth, just like any other tide. In other words, it would create heaps. That is what my illustration shows. The math and the illustration do not show an equal heaping in all directions. All points on the oceans would not swell equally, and at the same time. Therefore, if we had a barycenter tide, it would be quite obvious. It would create huge swells and it would swamp all other tides. We wouldn't need a list of 388 tidal harmonics, we would need only 1.

To add to the confusion, the National Oceanic and Atmospheric Administration (NOAA) explains tides on its website³ by disregarding fields and differentials altogether. In various places it glosses (very poorly) the effects I have calculated here. It mentions the barycenter effect, the tidal bulges, and so on, if only to mention all the physics thought to be involved. But after outlining and diagramming every possible cause and effect, it resorts to tides as a straight force from the Moon. The author states that the force is not great enough to overcome the gravitational pull of the Earth on the ocean water directly beneath the Moon, but at the tangents the Moon’s effect is unresisted by Earth’s gravity. Gravity does not pertain at a perpendicular. So the Moon tends to draw all the waters of the Earth from the tangents to the sublunar point. The author accepts that water must also “heap” at the antipodal point, but he does not say how an attractive force at the tangents would heap water at the antipodal point. In fact it would not. A force of this sort would tend to decrease the total amount of seawater in the far half of the ocean and heap it all in the near half. There would be no far tide, just a large far depression.

It is clear that there is no mainstream view of what causes ocean tides. Several views are held by different mainstream organizations. The NOAA is in the dark ages, CENPA is publishing some very dishonest math, and other experts are all over the map. Feynman, who no one would call marginal, weighed in on the barycenter explanation, but got it wrong. NASA and JPL appear to accept the inverse cube law, but avoid the issue on their websites. They give only PR glosses for a mainstream audience.
      The Standard Model, or its upper levels, appears to be currently founded on the inverse cube "law," but it is inconsistently applied. It is applied in conjunction with the centrifugal effects in regard to tidal effects on the Moon, but it is not when explaining tides on the Earth caused by Sun and Moon. This is because the current model needs to keep the Sun’s effects low, so that they do not conflict with data. In order to explain spring tides and neap tides, the Sun’s effects must be squeezed to fit data, and 67% is just too high; 45% is about right.
      Regarding the barycenter answer, it has not been accepted even though Feynman liked it. To disregard Feynman, physics has to have a pretty good reason, and I have shown you the reason. If we apply the correct math to the barycenter theory, then we find that if it is true it swamps everything. It gives us two high tides that vary 1/1.22, which we could readily accept. Except that these tides are so huge that all the other variations are lost. The neap tides and spring tides are easily measurable: the data can’t be explained if the effect from the Sun is 72 times smaller than the main effect. Lunar perigee and apogee variations also would become negligible if they were compared to a barycenter tide. All effects from variation in the lunar orbit would be lost.
      All this is a terrible problem. If you accept the postulates of current gravitational theory, then you are led inexorably to the barycenter tide. But you cannot accept it because it conflicts strongly with all data. It cannot be absorbed by even the most creative theory or math. But if you throw out the barycenter tide, then you have to throw out all the bathwater too. We used the same physics and the same differential equations to find the barycenter numbers that we did to find the Solar and Lunar numbers. If the physics and equations are wrong, they must be wrong all the way down. We cannot just go back halfway, taking the numbers we like. We have to throw out all the numbers and start over. Even more, we have to throw out all the assumptions. No matter how we followed the assumptions, we arrived at numbers that did not work. This is called a failed theory.
      Ask yourself why Feynman didn't insist on the barycenter solution. He was in a position to insist, and he was the type to insist if he knew he was right. He didn’t insist because it was only a suggestion, one he couldn’t ultimately make fit the data. He saw correctly that it was the logical answer given gravity, but once it didn’t fit the data, he gave it up. He was always an empiricist, and never let his theory get before the facts. Now, ask yourself why Feynman did not follow up with another theory. Surely he could see that gravity insisted on the barycenter tide. If the barycenter tide does not work, then there is something seriously wrong with gravity. The only way the barycenter tide could be false is if it is itself being swamped by another force field. What could this field be? Feynman obviously hadn’t a clue.

Tidal theory, like so much other contemporary theory, has become a farce. Newton proposed the Moon’s gravitational field as the cause of tides and no one has seen fit to correct him, even though we have data now that makes his theory ridiculous to keep. If Newton had known a mass and distance for the Sun and Moon, he would never have proposed the theory he did (I hope).
      Now, I admit that tidal theory has become very advanced in some ways. New models can predict the effects of tides with greater accuracy. And tidal theory is quite successful in showing how the given forces can create the tides we see. But it has made no progess since Newton in explaining the genesis of the fields themselves. As I have shown here, the foundational theory of tides is little more than a bad joke. The Standard Model tries to keep all this out of sight, and it is amazingly successful in doing so. Most tidal analysis does not mention the relative strengths of the fields of the Sun and Moon, since it immediately explodes the theory. Only places like Wikipedia are foolish enough to hang the dirty laundry in the open air. Most books and websites are long on computer graphics, historical glosses, and advanced mathematics, and very short on foundational theory. We can now see why.

Tidal Effects on the Moon

Now let us look at tides on the Moon. I will start over with my analysis, pretending once again that the reader knows nothing about tides; but in this section I will hit some topics that we missed in the first section. The Standard Model, as glossed in textbooks at all levels, explains tides by showing that real bodies do not behave like point particles. Because they have real extension, different parts of the body must be feeling different forces. If we take the Moon as an example, we can compare three points on or in the Moon. We take the point nearest the Earth, the point at the center of the Moon, and the point farthest away. The point at the center feels a force from the Earth that is just sufficient to make it orbit. That is why, in fact, it is orbiting. It feels no tides of any kind. The point nearest the Earth requires less force to make it orbit than the point at the center, but it actually feels more force. The point farthest from the Earth requires more force to make it orbit, but it is feeling less force than the point at the center. The point nearest therefore feels a resultant force toward the Earth and the point furthest feels a resultant force away from the Earth. This causes a tide that maximizes at the near and far points.
      So far so good. The Standard Model applied to the Moon follows what we have already found regarding the Earth. But before we analyze it again, let’s look at something interesting. Notice how theorists who claim to believe in General Relativity always revert to Newton when it comes time to explain forces in gravitational fields. In the chapters on General Relativity, we are told that an orbiting body is feeling no forces. It is simply following curved space, the “line” of least resistance. We are shown the ball-bearing on the piece of rubber, and the tiny marble orbiting it with no centripetal force. All quite ingenious, except that it does not explain the genesis of the forces at a distance used in tidal theory. How can an orbiter that is feeling no forces achieve tides? Even more to the point, how can an orbiter that is traveling in the curved space of its primary re-curve that space in order to transmit a tidal force to the primary? Is the gravitational field between the Moon and Earth curving convex or concave, relative to the Moon? I would think it must be one or the other. It cannot be curving both ways at once.
      If anyone answers “gravitons,” then I think we can throw out the curved space idea as superfluous. If we have gravitons mediating the force, then the Moon is feeling a force. In which case we don’t need curvature to explain anything.

But the current theory isn’t even that advanced, regarding tides. Graviton or no graviton, the theory reverts to Newton for the explanation. To cover all its bases, the theory gives the situation a sort of double cause. The first cause is given to the gravitational field. Nearer parts of the body will accelerate toward the Earth faster than farther parts, regardless of their weight or mass. Remember that acceleration in a gravitational field has nothing to do with mass. All objects fall at the same rate. Acceleration is dependent only on radius. So the analysis should always be talking about accelerations, not forces. This part of the theory is at least logical, given Newton’s equations. It is true that the static gravitational field would create tides as claimed, near and far. But it would create these tides even if there were no circular motion and no orbit. An object in freefall would experience this sort of tide, as the Standard Model admits.
      Current theory gives a second mechanism, and this mechanism requires an orbital velocity. Nearer parts of the Moon orbit in a slightly smaller circumference than farther parts. They travel this circumference in the same time as the rest of the Moon. Therefore they have a slower orbital velocity. With more acceleration and less orbital velocity, the near tide is increased. Likewise, farther parts of the Moon have less acceleration and more orbital velocity, once again increasing the proposed tide. This analysis is once again (mostly) true, but this second cause has nothing to do with gravity. It is an outcome of all circular motion, whether you have a gravitational field or not. Whirl any dimensionally consistent object and the circular motion will create tides in the object just like these, if you apply the forces in the same way.
      You will say that a spin dryer or a ride at the fair does not cause elongation like this, forcing the object to spread out along the radial line. Just the opposite: a fair ride or spin dryer causes the object to flatten out along the orbital line. But this is because all the force is applied from the back of the object. If we applied all the gravitational force from the back of the Moon, the Moon would also flatten in this way. No tide could be created at the back, since the force would constrain it, just like the wall of the dryer. The rest of the Moon would feel no force and would be totally unconstrained, except by its inner structure. Feeling no centripetal force, it would naturally follow the vector of the tangential velocity until it too was constrained by the force from behind or by internal structure. This is exactly what happens in the dryer or at the fair.
      But if Big Uncle Joe swings you by the arms, you do not flatten out like a towel in the dryer. You flatten out along the radius. The force is applied from the front, and you spread out in a line away from the center, with your legs flying behind you.
      To begin to create the Moon analogy, you would have to have three ropes along the same radial line. Lie on the ground with your head pointed toward Big Uncle Joe. He ties one rope to your hands, one rope to your waist, and one rope to your feet. As he swings you, Uncle Joe wants to keep your hands, waist and feet in the same line, so that your legs don’t lead, and your hands or waist either. From his point of view, he wants to see just your screaming face. Your waist and feet should be in a direct line behind your head.
      If your hands, waist and feet all weigh about the same, then it is obvious that the rope about your feet will have more tension on it. Your feet are going faster to keep up, and they weigh the same, therefore more force. By the same token, the rope on your hands has less force. Of course Big Uncle Joe is not a magician: he can’t swing you at three different rates at the same time. We can imagine the forces being different along each rope, but Uncle Joe is causing your tangential velocity at the same time, through the same ropes. He can’t impart three different torques down the same line. So this example cannot be created. It is a useful visualization however.
      A similar example could be created in the spin ride at the fair, or in a centrifuge. Take three equal weights and tie them to three separate points along the same radial line, at different distances from the center. Get the centrifuge up to speed and measure the forces. The greatest force will be on the one furthest from the center. To see how an object that was a sum of the three weights would react as a whole, subtract the force on the inner weight from the force on each one. The force on the inner one is now zero, the force on the middle one is bigger (middle minus inner) and the force on the outer one is biggest (outer minus inner). The outer weight wants to move away from the center a lot, the middle one less and the inner one even less. This is immediately clear with the outer one. If all three ties were cut simultaneously, then the outer one would move away from the center faster than the middle one. The distance between the two weights would increase. Therefore the outer weight seems to feel a force away from the middle weight. The same is true comparing the inner and middle, although it is a bit less intuitive for some. If the ties were cut the inner weight would move away from the center more slowly than the middle weight. Once again the two weights would increase the distance between them, so that there is a sort of force away from the middle weight once again. If the middle weight is the baseline, then both the outer weight and the inner weight will tend to move away from it. This will make the object deform along the radial line, just like the tides on the Moon.

So, we can add up the effects on the Moon just like on the Earth. We can use the equation
Δa_E = ω²r + GM[1/R² – 1/(R-r)²]
      = .000012 + .000024 = 3.6 x 10^-5 m/s²
Δa_S = ω²r + GM[1/R² – 1/(R-r)²]
      = 6.9 x 10^-8 + 1.4 x 10^-7 = 2.1 x 10^-7 m/s²

The solar tide on the Moon should be 171 times smaller than the terrestrial effect. More importantly, the visible tide on the Moon should be symmetrical front and back. Is this what we find? Not at all. The Moon rotates relative to the Sun, so we would not expect to find a solar effect on the Moon, beyond a tiny constant shift in the crust opposite the direction of this rotation. The rotation of the Moon on its axis relative to the Sun does not cause a further tide from the Sun, or add to the tidal effect, but it acts to shift the tides we have already calculated, just as the rotation of the Earth shifts the ocean tides, causing them to travel. I am not aware of any experiments on the Moon to measure lateral shift of the crust in the direction opposite rotation, to verify the relative strength of the solar tide, although this would be a very useful experiment. However, concerning the terrestrial tide, we have ample visual data. 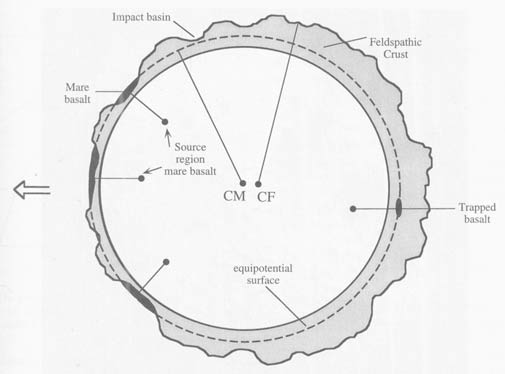This data is not a confirmation, to say the least. The schematic of the Moon (above) will show you that the Moon exhibits no real tide at the back. Even more astonishingly, it has a negative tide at the front, the crust being almost obliterated in places. How does current theory explain this? It can't explain it using gravity or circular motion. This is how it is explained in the Encyclopedia of the Solar System:⁴ "The conventional explanation for the center of figure/center of mass offset is that the farside highland low-density crust is thicker. It is massive enough and sufficiently irregular in thickness to account for the effect." More gobbledygook, in other words. If the farside crust is low-density, this would only add to the problem. To create a greater tide we need more mass over there, not less.

Before I move on to solve all these problems, I have one more thing to say about the orbit of the Moon. In all these analyses, both mine and those of the Standard Model, it has been assumed that outer parts of the Moon can travel faster than the inner parts. The diagram requires it and so we have just taken it as a given. We do not even ask how it is physically possible for different parts to have different tangential velocities and different orbital velocities. The gravitational field cannot be creating them, since it cannot exert a force tangentially. The field creates only radial forces. We need either a mechanical cause of the variance, or we need to show that all orbiters exhibit shearing along the direction of orbit. Orbiters in tidal lock should exhibit strong symptoms of shearing, since the forward part of the object is always in lower orbit and the back part is always in higher orbit. The back part of the Moon should shear in the reverse direction of orbit and the front part should shear in the forward direction. But the data is negative, and we are given no cause for the negative data. The only mechanical cause would be some sort of absolute rigidity of the Moon radially. But this is not true empirically. With current theory, the lack of data is a complete mystery.
      General Relativity can explain it, since according to that theory, the Moon is feeling no forces. A Moon feeling no forces would not be showing any signs of shearing. But you can hardly use GR to explain the tides we don’t see and use Newton to explain the tides we do see. The Moon is either feeling forces or it isn’t.
      The problem was a big one for Newton, even in his own time, since he is the one who postulated that the tangential part of the velocity in orbit was caused by the orbiter's "innate motion". That is to say, the tangential vector is one the object has prior to or independent of the gravitational field. But of course the object could not have a variable innate motion. It cannot speed up outer parts and slow down inner parts just to suit diagrams.
      It is now not just Newton’s problem. Current theory has inherited it and failed to explain it, or even try to explain it.

You can now read my newest paper on tides, More Trouble with Tides. You can also read the first two parts of my Solution to Tides.

¹www.npl.washington.edu/AV/altvw63.html. This site is managed by CENPA, the Center for Experimental Nuclear Physics and Astrophysics.
²www.sanho.co.za/tides/tide_theory.PDF
³www.co-ops.nos.noaa.gov/restles1.html#Intro
⁴Compiled by NASA and JPL, 1999. p. 252.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.