go to homepage
go to updates
go to short calculus paper

Trig Derivatives found
without the old Calculus

now including a disproof the chain rule

by Miles Mathis

First written October 2006, extended greatly June 2015

Be sure to read the addendum, where I show the current proof for the derivative of (sinx)² is fudged. I show that the mainstream long ago pushed the proof via a misuse of the chain rule.

Since I first published my very long paper on the calculus several years ago, I have gotten many angry emails like this one:

You are wrong! Mathematics is a science about numbers. Graphs, plots are for illustration—you can prove nothing from them.

y = sin x

y' = cos x

How do you prove that by your method?

Yuri

Even my mother, who is a professional mathematician, has failed to see how I can incorporate my table into an analysis of all functions. She never got angry, but she has used my silence as proof that my method has limited use.

Now, I said in a footnote to that paper that my method applied to all of calculus and all functions, not just differentials or polynomials. It applies to trig functions, logarithms, integrals, and so on. I assumed that anyone who understood my argument would see that immediately. I didn't even bother to write a follow-up paper on integration, it seemed so clear to me that anyone could just read up the tables instead of down. I was busy with other important problems and decided to let that paper hang, along with any paper that specifically addressed trig functions. Frankly I had hoped that someone might come along and see my point, and that they would do the dirty work of advancing my theory into these other alleys. Once I have solved a problem, I tend to get bored, and stating the obvious does not really inspire me to write.

However, I now see, years later, that I was mistaken in assuming that my initial paper would penetrate into the mathematical community. It has been turned down for publication in all the top forums, for what I think are political reasons. So I have recently gone back and simplified my argument, self-publishing a shorter and simpler paper, argued in what I consider to be an extremely transparent manner and language. I hope that this paper may eventually make some headway in the mainstream, even if I continue to be blocked by the higher-ups.

Beyond that, I have decided to publicly solve Yuri's trig problem for him, knowing full well that it won't be the further miracle anyone needs. No matter what I do or how I do it, I now expect most of the status quo to find a way to dismiss it out of hand. They weren't bothered by the fact that the current equation has been hanging from skyhooks for 350 years, and so they won't be impressed to see the equation finally grounded. Anyone who studies my table and doesn't undergo an epiphany is someone who is pretty much unreachable, and solving this trig problem with the table won't reach them either. But here goes.

So, Yuri, watch closely, my friend. I will do it so quickly and so easily, you will no doubt think it is nothing. I will show you how to do it without limits, without going to zero, without infinite series, and without the current derivation of the calculus. I will do it using only my table of exponents and the constant differential.

We start with this equation, which is one of the defining trig equations:

y = sinx = ±√(1 - cos²x)

Notice that we are still dealing here with exponents. The cosine is squared and that is the important fact here, not the fact that we are dealing with trig functions. From a rate of change perspective, the trig function is meaningless. A sine or cosine is just a number, like any other. It is written as function of an angle, but that does not affect the rate-of-change math at all. The cosine of x is a single variable, and we could rewrite it as b if we wanted to, to simplify the variable for the rate of change math. Likewise, we could rewrite sin x as a, if we desire. All we have to do is make sure we don't confuse sine and cosine, since they vary in different ways, but we can mark them anyway we want.

Let a = sin x

b = cos x

Therefore, we could rewrite the equation as

y = a = ±√(1 – b²)

Square both sides

y² = 1 – b²

Since sine and cosine are co-dependent, we can differentiate either side, or both sides, starting with either side we like.

Let z = 1 – b²

z = y²

Δz = z' = 2y (from my table of integer exponents)

Δ(1 - b²) = 2y

Now switch sides and differentiate again

2y = Δ(1 – b²)

2Δy = 2y' = 2b (once again, straight from the table of exponents)

y' = b = cos x

[For a slightly more expanded proof in the same vein, you may wish to consult my new paper on the derivative of sin5x. It may clarify some of the steps above for some readers.]

You will say that I just followed normal procedure (a kind of chain rule), but I didn't, since whenever I use the equation nz^n-1 = Δzⁿ I pull it from my table of exponents and constant differentials, not from current sources, which I have shown are all faulty. I prove this equation using a constant differential, not a diminishing differential or a method using limits. My table shows that with the exponent 2, you only have to go to a third sub-change in the rate of change chart in order to find a straight line, or a constant rate of change. This means that you aren't anywhere near zero, and aren't anywhere near an infinite series of any kind. You are two steps below the given rate of change for this problem (which is an acceleration or its pure math equivalent) and two steps is two steps, not an infinite number of steps. In any rate of change problem, we simply aren't dealing with infinite series, points, or limits. We are dealing with subchanges, and we are seeking a line of constant differentials. Not a point, a line. This is why my method is so important.

It does not matter in this problem that the curve was created by sine or cosine. The way the curve was created does not concern us in calculus. All we need is at least one dependence. If we have that dependence then we can use the definition of exponent and integer to create the table, and that table will straighten our curve out in a definite and finite number of steps—the number of steps being absolutely determined by the exponent itself.

An infinite series is only created by an infinite exponent. But an exponent signifies a change, and a change requires time, so that an infinite exponent would imply infinite time. We do not need to solve equations concerning infinite time, not in physics and not in mathematics. Therefore we have no need of infinite series in rate of change problems.

Now to briefly answer Yuri's other concern (from the first paragraph). If you will remember, he ridiculed me for studying graphs and real-world situations in trying to understand math. Hopefully you know see that my analysis of the Cartesian graph (in my long paper) was necessary to discover the problems within the calculus, and that therefore this analysis certainly transcends "illustration". I never claimed that calculus was all about graphs, or implied that the graph was the central feature of either calculus or of my argument. But I would never have discovered what I did without an in-depth analysis of the graph and the way the curve is created there, and I could never fully explain my method without using the graph to make it clear. Trying to understand the calculus without looking at graphs and real motions would be like trying to understand trigonometry without looking at triangles.

[Addendum, June 8, 2015: I just got a complaint from a person claiming to be a highschool student, accusing me of an error here. I don't believe the complaint was really from a highschool student, since she seemed entirely too sure of herself ( and nasty) for someone that age. But I will address the complaint nonetheless. The complaint was that I seem to be implying that the derivative of (sinx)² is 2sinx, when of course it isn't. In an intermediary step, I differentiate y² to find 2y, and y² is supposed to be equal to sinx. Although the mainstream currently does exactly the same thing in the first part of the chain rule (see below), she told me I have broken a rule of math. I tried to explain to her the difference between differentiating and finding a derivative, but she wasn't listening. She was so sure I was wrong, I have to wonder why she wrote me to ask for my response. She didn't want a response, so why write? But I will see if anyone else out there can comprehend the difference. I expect that few will, since the difference is not taught in any school I know of.

To start with, I send you to the current and mainstream proof for the derivative of (sinx)². To find this derivative, one normally uses the chain rule. To apply the chain rule, you are instructed to first “take the derivative” in the disallowed way. In other words, you just drop the 2 down in front to find 2sinx (which I was told was disallowed above, in my proof). Next, you find the derivative inside the parentheses. Since the derivative of sinx is known to be cosx, we multiply that by what we already have, obtaining the final result 2sinxcosx. Curious, isn't it, that the mainstream can use multiple steps in its chain rule, but I can't use multiple steps in my own method? What is stopping me from making the same complaint against this proof that was made against mine above? Why can't I just pause the mainstream proof after step one and complain that the derivative of (sinx)² isn't 2sinx? To avoid that complaint, the mainstream normally (or often) doesn't call that first step taking a derivative. Although it is exactly the same manipulation, they just call it the first step in the chain rule. Because they have given it a different title, you aren't expected to notice it is exactly the same manipulation.

But back to my proof of the derivative of sinx. Notice that to “find a derivative” here, we have to “differentiate” twice, in both directions. That should seem odd, since normally when we have a function to the power of two, we only need to differentiate once to find a derivative. We only have to look at one rate of change, right? Well, you aren't taught it that way, but that is what is happening. But in this functional equation we are looking at, we have both sine and cosine, and both are to the power of 2. We don't just have one function, we have two interdependent or co-dependent functions, and both are squared. And that is why we have to look at rates of change on both sides.

Now, admittedly, that is not the way these problems are normally solved. But I am not claiming to solve these problems in the normal ways, am I? I am claiming to solve them in a new way. So complaining that I do not follow old rules is sort of missing the point. I am showing that the old rules are sometimes wrong and sometimes unnecessary. Yes, sometimes they are necessary, especially if you don't know what is going on with the rates of change. In that case, you are best to stick to the old rules. But if you know the difference between slopes, derivatives, differentiation, and rates of change, you can simplify the math considerably.

To see this in another way, notice that I never claim that the derivative of (sinx)² is 2sinx. I only claim that you can differentiate y² to find 2y, even while y = sinx, provided that do not stop there. You must also differentiate in the other direction, because if you don't you will not have related the two rates of change to one another at the same time.

In other words, I am not claiming that the derivative of (sinx)² is 2sinx. I am claiming that the rate of change of (sinx)², taken alone or in isolation, can be written as 2sinx. But since sinx is, in fact, never found in isolation, to find a derivative you have to keep going. You have to find the rate of change of cosine simultaneously, you see. Which is why I differentiate in both directions.

What my critic is doing is stopping the proof between the two differentiations, and saying that because my first differentiation didn't achieve the known derivative, I have cheated. But that is to completely miss my point. Of course the first differentiation wouldn't find any known derivative, since it is only half a manipulation or half a relationship.

Let me continue. My critic might say, “Well, if that is so, why can't you just insert (sinx)² into the basic derivative equation to find the real derivative? Why exactly is it allowed in this interior differentiation, but not allowed in that direct way?” Because if we are seeking the derivative of (sinx)², we aren't just seeking the rate of change of sinx by itself. We can only drop the 2 down like that in cases where we are dealing with one rate of change. But as we have seen, sine and cosine are fatally linked at all times. We saw it in the very first equation, sin²x = (1 – cos²x). And we see it after we find the derivative of sin²x, which is 2cosxsinx. That just tells us that whether you are given both or only one of the two, you have to monitor both rates of change. If you were to just drop down the 2, you wouldn't be monitoring both rates of change, and you would get the wrong derivative. But I am not doing that in my proof, am I? No, I am explicitly monitoring the rate of change in both directions (albeit in a somewhat compressed manner). Which is why I get the correct derivative at the end (or the absolute value, at any rate—the negative sign can be found by monitoring the relative directions of change)*.

This analysis is borne out if we look at the current proof that the derivative of sinx is cosx. Unlike the proof for (sinx)², the proof for sinx cannot be found by any chain rule, obviously. The proof is actually extremely long and unwieldy, as you see if you take that link or study any other similar site. Strictly, it is exactly as complex as the proof of the calculus itself, since it relies on the same basic “identity”—an identity that itself relies on the infinitesimal h. It is precisely this reliance on infinitesimals that I am trying to skirt with my new method. At any rate, in this proof you can see that sinx can never be monitored by itself. Every proof of sinx must include cosx, and the reverse. They aren't just dependent functions, they are interdependent functions. Both have to be monitored at the same time, because the slope of one is always determined by both functions.** Which is why I started with the equation stating their interdependence, and why any proof of the derivative of either function must start with an equation that includes both.

I will argue that the chain rule (used in the current way) is the fudge, and that my method is the correct one. I hope you can see that applying a chain rule in this way to trig functions is actually very slippery. You are being to taught to basically make two different manipulations on the same entity, but not being told why. There is no chain here. There is only one link, that being sinx. Or, if you wish, we have two links, but both of them are sinx. We see that if we write the square out in long form:

(sinx)(sinx)

Why would you take the derivative of one of those terms, but not the other? It appears to me that we are actually taking the derivative of one of them, then multiplying by a term that is not really the derivative of both together. Why on earth would we wish to do that?

To see what I mean, notice again that when I solve these trig functions for derivatives, I make sure to manipulate both sine and cosine at the same time. But when they apply the chain rule to (sinx)², they aren't doing that, are they? They aren't looking at cosine at all. They are trying to differentiate sinx twice, in two different ways, which is why I could immediately see they were pushing the proof.

We see that again by the fact the chain rule was meant to apply to a functional relationship inside a functional relationship, as in the equation

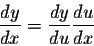
Or the equation

The derivatives of simple trig functions don't fit that form, as we can see even more clearly when they try to use the chain rule on a term like sin5x. They write it as sin(5x) and then try to use those imported parentheses to convince you they suddenly have a chain of functions. They tell you g(x) is 5x and sin(x) is h(x). But that is an obvious push, since to split the term that way implies sin5x can be written as two numbers. It can't. The sin5x is only one number or one variable. One number can't give you two functional relationships. There is no real “interior” and “exterior” here, since the sin signifier as written is neither a power signifier nor any other sort of multiplicative signifier. Sin with its variable is one term, and it cannot be split into two sub-functions. So the proof is just a fudge from the get-go.

Actually, the only reason you are being taught this faked mainstream proof is that it works. It is a push that gives you the correct result. And they have to push the proof because they don't understand what is really happening.

I will now tell you what is really happening, and it has nothing to do with a chain rule (or not the given chain rule, at any rate). To discover it, we have to go back to my proof above, starting with the equation

(sinx)² = 1 – (cosx)²

Since we are seeking the derivative of (sinx)² instead of sinx, we need to start by differentiating the right side instead of the left. That gives us

Δ(sinx)² = -2cosx

But, as we have seen, that can't be the full manipulation, since we have found a rate of change of cosx but not of sinx. We have monitored cosine for change but not sine. So what we need is the rate of change of (sinx)² with respect to sinx. Or, to say it another way, we need to compare Δsin² to sin. That is a sort of chain rule, but it is a very different chain rule than the one you are taught. To do that, we don't even have to differentiate: we simply divide the left side by sine, which gives us this:

Δ(sinx)²/sinx = -2cosx

That fraction, by itself, tells us how one term changes relative to the other. That is what a fraction is, in this case. You may think of it as one of those “with respect to” fractions if it helps you, but even that isn't really necessary.

We can then move the sinx over to obtain this:

Δ(sinx)² = -2cosxsinx

Since we know the rates of change are opposing*, we can use that knowledge to drop the minus sign, giving us

Δ(sinx)² = 2cosxsinx

Since in this case, my Δ is indicating the same thing as the current derivative (both are indicating a rate of change), my proof is complete. I have matched the finding of the mainstream without using their fudged chain rule.

Also notice that I have explained each step. When have you ever been given a reasonable explanation of the chain rule as applied to this proof? There can be no reasonable explanation of the current chain rule as applied to this problem, because, as we have just seen, they totally ignore cosine in the proof. They manipulate sinx twice, in completely illogical ways. Cosine comes into the current proof only as a manipulation upon sine. In other words, they don't currently monitor any slope of cosine in order to solve. That cannot work, since to solve any trig derivative or slope, you have to monitor both sine and cosine.** In my proof, I monitor the change of sin² against both cosine and sine, as you see.

I also draw your attention to the fact that the 2 actually enters the last equation above with the cosx, not the sinx. Which again proves the chain rule was a fudge in this case. We also see that the sinx in the equation isn't the derivative of anything. It wasn't found by taking a derivative or by differentiating. It is just a straight relationship, as in any other fraction. You could say it that it is found by a form of calculus, since the relationship of sin² to sine here is a “with respect to” relationship. But what I mean by saying it isn't the derivative of anything is that we don't have to manipulate powers in any way. We just write the relationship as a fraction.

[You may consult my next paper for clarification of the above proof. There, I make clear what some may already comprehend: I am basically scaling my solution to sinx. So although it may look like I am illegally dividing only the left side by sinx, that isn't what is happening. I am scaling a completed equality to an external function.]

So while it may seem I have broken some great rules in my first proof of sinx, I actually haven't. I have just used the given and longstanding manipulations in a more direct manner. In doing so, I have greatly simplified the old proof. Ironically, the ones who have broken rules are those who try to insert sinx here in the middle of my manipulation, claiming I have found the wrong derivative for its square. But since I am finding the rate of change of sinx in isolation in that step, not its derivative, this entire argument against me is another strawman argument. As we have seen, they manufacture that strawman to use against me, but do not use it against their own chain rule.

More importantly, we have found that the mainstream is making up fake chain rules to suit themselves, and that they have been doing it for centuries. Although I am not making a blanket argument against the chain rule here, I have certainly shown the rule is fudged in this particular proof. [We will see it is fudged in other trig functions in upcoming papers, so this is not an isolated case.] A bastardized form of the chain rule was used here to push this derivative of (sinx)² to the known number. But, as we have seen, both manipulations in the chain rule were manufactured. In neither step were the proper relationships between functions discovered, and the 2 was completely mis-assigned.

It would be interesting to see who first fudged this proof of (sinx)², and how long ago. I suspect it has been sitting out in the open since the time of Euler, but I could be wrong. Someone else will have to do the research in this case, since I have other more pressing things to attend to. But it is just more proof that both math and physics have been unmoored for a very long time. What we had been sold as bedrock is actually just a cardboard foundation cast over a vast abyss.

To sort of bookend this addendum, I will answer one last question. I will be asked why I can differentiate (sinx)² to find 2sinx (as in my first proof), but the mainstream can't. Haven't I claimed their method was a fudge, and that it was a fudge due to the fact that the chain rule requires a chain of correct derivatives? No, I never said that. I said the chain rule was misused with this trig function, but not for that reason. It is fudged not because that is a fake derivative, but for several other reasons, including the fact that the mainstream is creating a fake chain by misreading the parentheses, and the fact that they are failing to monitor both sine and cosine.

I suppose I should be grateful for this latest email, since it gave me an idea of the many ways I am being misunderstood. It appears that some readers are coming to this paper without making an effort to read and understand my longer paper on the foundations of the calculus. That doesn't really surprise me, since I get these isolated strawman arguments against many of my ideas, always from people who have made no effort to comprehend what I am trying to do. They tell me I am breaking their teachers' rules, expecting me to be chastened, but that just means they haven't even comprehended my titles or my basic intent: that is exactly what I am trying to do. I am breaking all the old rules on purpose, because I have proved the rules are false or faulty. I don't really understand why those who are content with all the current rules would even click on my papers. If they are so confident in what they have, they are welcome to it. It isn't working worth a damn in the real world (see physics), but they have never been too concerned with that, as we know.

More than that, I should be thankful for this latest email, because it made me angry enough to return to this paper and extend it into an even stronger argument against the status quo. This pulling apart of the proof of (sinx)² was long overdue, and I might never have done it without the prodding of this clueless schoolgirl.]

*Some won't understand what I am doing there, so I will clarify it with a simple diagram.

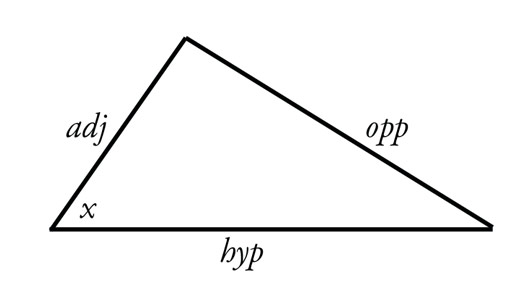
Cosine is defined by that adjacent leg of the triangle, while sine is defined by the opposite leg (both relative to the hypotenuse, of course). If we draw the hypotenuse flat to the horizon, then we can “see” the relative slopes of sine and cosine. If we think of those upper legs like a roof, one slopes up while the other slopes down, right? You may ask, how do we know which is which? Aren't “up” and “down” relative terms? Well, we have to put the triangle in some sort of Cartesian graph, which specifies a direction. Once we do that, with right indicating positive direction, say, then if one leg slopes up, the other slopes down. Although this visualization is, as usual, a simplification, it is useful when trying to understand sine's relationship to cosine.

**Now, to find the slope of the opposite leg, say, rather than its length, you can't just monitor sine alone. You can't build a triangle with two sides, as the old saying goes. You also have to monitor cosine. Why? Because if you are just given a term like sinx and asked to differentiate, you don't actually have enough information to solve. And I don't mean solve as in find a specific number. I mean you can't solve because you don't have enough information to build a real derivative equation or find a general slope equation. You don't, because you aren't given the length of the hypotenuse, for instance, or even a variable for it. Without information about the length of the hypotenuse, one leg of the triangle with its angle isn't enough to tell you any possible slope of sine or cosine. Just consult the image above. Say you are given sinx. That gives you possible values for x and for the length of the opposite leg, right? Now, if you also have a possible value for the length of the hypotenuse, you could write an equation for the slope of sine, since you then have enough information to build your triangle. Given all that information, there is only one way you could draw in the adjacent leg to fit. In that case, for each value of x and sinx, there is only one value of cosx. But if you are not given any possible value for the hypotenuse, you can't solve, since the adjacent leg could be any length. And its length will then determine the slope of sine.

That is why I started with the equation sinx = ±√(1 - cos²x) in this paper (in both proofs), and why any proof of the slope or derivative of either sine or cosine must start from an equation that includes both.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.