return to homepage The Difference between The deeper I get into all these problems, including the problems of General Relativity, Quantum Mechanics, calculus, and basic physics, the more I realize that one of the most fundamental problems beneath all these is an ignorance of what acceleration really is. Historically, the concept of acceleration has been foggy and its definition has been incomplete, and that is true to this day.
return to updates
Squared Velocity
and Acceleration

I didn't realize the extent of this until last year. In studying the textbook solutions for “variable” acceleration, it became clear that the authors themselves didn't know what they were solving, either as a matter of mathematics or as a matter of definitions. More recently, this became clear when I delved more deeply into the difference between squared velocity and acceleration. I thought maybe someone somewhere could tell me a physical difference. They have different dimensions, so they should be physically different. However, in studying the historical texts, the modern texts, and in asking around, I found that no one really knows or ever did know. Sometimes they are treated as different and sometimes they are treated the same. If you search online, you will find absolutely nothing.
I came up against the problem in a recent paper, when I couldn't get my dimensions to cancel, using both accelerations and squared velocities. I knew I had the right answer, but I couldn't justify my dimensions to myself or my readers. Finally it occurred to me that this was because the current dimensions simply weren't correct. Once I figured it out, I tried to point this out to my readers in that paper very quickly, but it didn't work. The explanation requires a paper to itself.
The primary problem was that I was multiplying a meter times a meter, in the dimensions, and this was giving me a square meter, of course. In the same way, a velocity times a velocity is now considered to be a squared velocity. But does that make any sense? In looking closer, I saw that it didn't make any sense at all.
To start with just the meter: a meter is a distance, so when we multiply a distance times a distance, what do we get? Assuming we are in a straight line, we can only get another distance. That is, if the two initial distances are vectors in the same line, then the quotient can only be a distance. It cannot be a square distance. What the hell is a square distance? If we are in a line, it is meaningless. The only time that a square distance can have any meaning is if the two initial distances have an angle to them. In that case, our answer may be an area, which is a square distance. For instance, if they are orthogonal, then the “square distance” is telling us that we have two distances in two unequal dimensions. We have to keep track of both vectors, with angles or in other ways. But if both distances are in the same line, then they are in the same dimension, and in that case “square meters” just means the same thing as “meters”. The “square” part of that has no content. In a line, there is no such thing as a square meter.
In the same way, if two velocities are in the same line, then when you multiply them together you will get an acceleration. An acceleration is two velocities in the same line, multiplied together. An acceleration is currently defined as a change in velocity, but what does that mean, as a matter of mathematical symbols? Well, it doesn't mean that two velocities are added, because if you add two velocities you get a bigger velocity, not an acceleration. No, you have to integrate the two velocities, and, if you do it right, an integration can be represented by a multiplication.
This means that a (power 2) acceleration is two velocities integrated over time. An acceleration is the motion of a velocity, which means it is the velocity of a velocity. In the end, an acceleration IS a squared velocity, as a matter of dimensions. But we are correct to drop one of the meters in the numerator, since the velocities have to be in a line.
As it turns out, all power 2 accelerations are in line. To create a curve, you have to have three velocities, and therefore a power 3 acceleration [see my break down of the orbital curve in my paper on π, or see below]. Because the velocities are in a line, the meters are in a line and cannot be “squared.”
You will scream at me that an acceleration, even to power 2, is always a curve on a Cartesian graph; but while that is true, it is not to the point. A Cartesian graph is a simplification of reality, not a full representation of it. What curves on the graph will not necessarily curve in real life. Just think about it for a moment. Say you are given two velocities, and you are given that they are not in a line. First, let us add them. Do we get a curve? No, we get a line, as below.
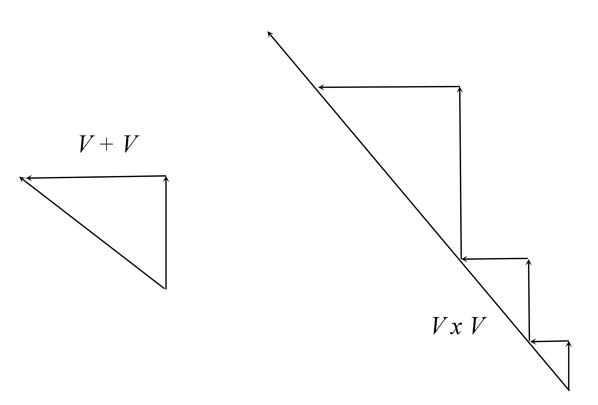
Now, instead of adding, we multiply the vectors. What does that look like? It looks like the second figure. Still a line. An accelerating line in length, but not a curve. As I said, to get a curve, you have to have three integrated velocities, plus at least one angle. The circle or orbit is three velocity vectors integrated. Yes, I have shown in great detail in other papers that the orbit is actually a cubed acceleration, with three t's in the denominator.
This means that, at its simplest, an acceleration is just a squared velocity where both velocities are in the same line. We then drop the extra meter in the numerator, since it isn't needed. In fact, it is false. The dimension is a length, not a squared length. There is no such beast as a squared length.
But, as I just showed in the second figure, an acceleration can also be a squared velocity where the velocities are NOT in a line. The only additional problem there is that to get the right number for the magnitude of that acceleration, we have to keep track of the angle between the two velocities. We have to know it and we have to put it into the equations. But even then, the acceleration will not have a square meter in the numerator. Once we correctly integrate the velocities using the angle, we can drop the extra meter.
Therefore, every time we have a velocity times a velocity in the same line, and we are integrating the velocities, either by using actual integration, or by indicating the integration by the proper multiplication, we can drop the extra meter. This also applies to velocities that are not in a line. If we are integrating them properly using the angle, then we can drop the extra meter. A square meter indicates an area, and if we aren't calculating an area, then the square meter is both meaningless and false.
In my paper on v=at, I used this example of integration, to show we have the same dimensional problem with integration:
∫(2x + y)dx = x(x + y)
We integrate a sum but get meters squared. I pointed this out, but I don't think anyone understood me. The value (2x + y) is a length, is it not? If x and y are lengths in the same line, then the sum is also a length. Well, if we integrate a series of lengths, we can only get a larger length. It doesn't matter if this series of lengths is infinite or not. That integral must be a length. In which case the dimensions of x squared will just look curious.
I am sure that many readers reading that first paper looked puzzled and wondered if I was crazy. The integral is commonly interpreted as the area under a curve. And of course an area does indeed have square dimensions. But that curve and area are both on a Cartesian graph, and with the Cartesian graph, x and y are orthogonal. They are at 90o. In that case, yes, the integral will be an area, and the square dimensions make sense. But in physical problems, x and y do not have to be orthogonal. Descartes put the two dimensions at 90o in order to make many relationships clearer. If we had both x and y in a line, numbers would overlap and it would be confusing. So the graph is a convenience. But it is not a necessary representation of the physical world. In fact, in all cases the Cartesian graph is a falsification. The amount of the falsification only varies depending on the problem. If x and y really are orthogonal, then the Cartesian graph is only a slight falsification. If x and y are in line in the real world, then the Cartesian graph is a serious misrepresentation.
You will now say that x and y are orthogonal, since they are usually defined as width and depth or something. They are assigned to orthogonal vectors in the real world. Yes, often they are. But not always. We have to remember that x and y are just variables, and no angle between variables is assumed in integration. For example, say we are studying the growth of whales. We assign x to the length of the head of the whale at birth and y to the length of the body. We separate them out this way because, perhaps, we are also interested in how much bigger the heads of baby whales are, compared to adult whales. We get a chart of values for x and y over a span of years. Obviously, the numbers will be changing in the same line. Later, for some weird reason, we might want to integrate (x + y), or some other combination of the numbers. We might want to measure the distance to the Moon using the lifespan of the whale. Who knows, scientists are weird. Well, in that case, the integral will be a distance, not an area. You can't get an area from two numbers in a line.
If we apply this to my muon problem, in which I was applying the equation v = v0 + at, we find that the motion of the muon and the motion of the gravity field of the Earth are in line. There are no angles between the velocity of the muon and the acceleration of the field. The muon is traveling straight down to begin with, and the Earth is pulling straight down. No angles, and no areas. Therefore, when we integrate the velocity with the acceleration, we get too many meter dimensions in the numerator. This is not because we need to add tricky constants in order to correct the dimensions. No, it is just because we need to dump some of those extra meter dimensions. Every time we multiply a velocity and a velocity that are in line, we have to dump one of the meter dimensions. We do that because two velocities integrated are just an acceleration, and an acceleration only has one meter in the numerator.
Therefore, my dimensions in this equation do resolve:
vf = v0 + 2v02t + av0t2
Since we have only one meter dimension in each numerator, each term resolves to a velocity. A squared velocity is an acceleration, so 2v02t reduces to a velocity. And a velocity times an acceleration is a cubed acceleration, of the form m/s3, so the term av0t2 also reduces to a velocity.