return to homepage The Third Wave
return to updates
A Redefinition of Gravity
Part V
The Aberration
of Starlight
and other problems
by Miles Mathis
milesmathis.com
mm@milesmathis.com
The aberration of starlight was historically considered the most convincing data in support of Einstein's curved space hypothesis.* He is said to have predicted it, have given us a number for it, and it was found to be so. It must be noted that Newtonian physics also implies the bending of starlight, once light is known to be a particle. Newton’s gravity will affect light just as much as General Relativity. Newton said so explicitly. You don’t need curved space for the aberration of starlight, you only need light to have a mass equivalent. Eddington even did the math and found his own number for this.
However, it most be noted that Einstein originally got the wrong number for both the bending of light by the sun and the precession of the perihelion of Mercury. In his first equations, he found less than half the known amount for Mercury and exactly half the correct amount for the sun. He corrected his number for Mercury up, to match the known number, so this was not a prediction. It was a postdiction. This correction to the field equations doubled his prediction for the sun. This might be considered a true prediction, in a way, since the number for the sun was unknown at the time. But it is important to realize that this "prediction" was mathematically linked to the postdiction on Mercury. If Einstein had not known the number for Mercury, he would never have known that he needed to correct the math. It is interesting to realize that his underlying theory allowed either number--either his first number or the doubling of that number. So his claim that his math evolved perfectly out of unquestionable axioms is completely false.
Both Newton and Einstein postulated the existence of a field produced in some mysterious way by the sun. Newton thought matter in the field felt a tug; Einstein, that matter followed a curved path, without a tug. In my paper on General Relativity I offer a third view, a view that turns both "fields" inside out.
In my paper on Celestial Mechanics I showed that the production of an ellipse with a ball and a rubber band produced a field that was inside out. It was backwards. The force on the rubber band must be greater at apogee than at perigee, which is the opposite of a gravitational field. The "field of the rubber band" varied with the inverse square law, but it got stronger with greater distance, not weaker. Now I refer you to Einstein's chapter [ch. XX] on gravity in his book Relativity. After showing the equivalence of gravity and acceleration (with his elevator car in space), he said, "Now we might easily suppose that the existence of a gravitational field is always only an apparent one." But, he continued, "It is impossible to choose a body of reference from which the gravitational field of the earth vanishes."
Einstein’s elevator car is the thought problem that led me to work seriously on expansion theory. I asked myself, can we explain the gravitational field of the sun as caused only by motion, and can we explain the bending of starlight by this motion? Einstein said no, because he didn't want to propose expansion. I have changed that answer to yes to see if I could answer all the questions that arose. So far I have done well. So let us continue and see if we can explain aberration.
It turns out that aberration is among the simplest things to explain with expansion. Let us say we have data before us that shows that light from a star on the far side of the sun has not arrived on earth in a straight line. It has curved in getting to us. How do we come to that conclusion? Simple. Before the light from the star got to the sun, it was travelling in line x, the line it always travels in when not affected by the sun. From the sun to the earth, it was travelling in line y, roughly. The difference in the lines is the angle of refraction. Now let us ask, is there any other possible movement that could explain this "refraction." There is one other, though no one has ever put it forward: Something besides the light has moved. You will say, what? What else could have been refracted?
Well, nothing else is in a position to be refracted or bent, but there are a couple of other movements that could explain the appearance of a bending of starlight. At first I thought that the expansion of the sun would explain it most easily. I soon decided against that. But I will let you see the steps that led me to my final explanation.
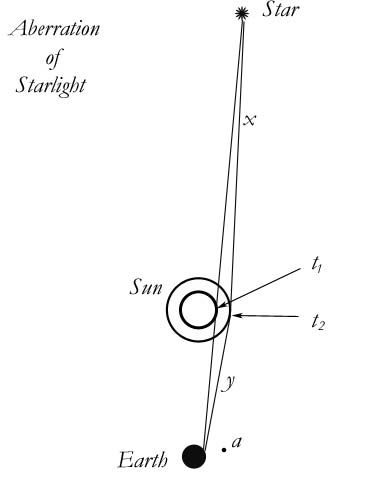
I have diagrammed an expanding sun here. Look at the starlight arriving at the earth. From the vicinity of the sun to the earth you have "seen" it move from right to the left. You expected it at point a, it arrived at point b, on the earth. Therefore you conclude that it must have been refracted. But now go to the background of this movement. What is the beam of starlight refracting relative to? What is the light moving with regard to? The sun, of course. Either the beam of starlight has moved from right to left, or the right edge of the sun has moved from left to right. In other words, the sun has moved into the space that the beam of light just passed. The light was not refracted, the background moved. The sun is the background, and it moved.
The aberration of starlight is either 1) the sun was still and the light moved to the left after it passed the sun, or 2) the light traveled in a straight line and the sun moved to the right after the light passed it. History has chosen 1). I choose 2).
Obviously the right edge of the sun cannot move by itself. The sun cannot just shift to the right for no reason; nor can the sun bulge on the right side and leave the left side standing. So what I have theorized is an expansion of the sun, as a whole, in all directions. From the time the starlight hit the vicinity of the sun until the time it reached us, the sun grew a tiny bit. This “bit” is the same bit that the starlight is supposed to have refracted.
Some scientists have looked quickly at my figure above and said, "That won't work. According to your diagram, we should see the star with the sun as its background—meaning, not at all. It would be lost in the sun. Or, during a total eclipse, we would see your star within the circle of the eclipse! You are saying that the light from the star is not curved or refracted; that there is no aberration. You are saying the light is arriving from the star to the earth in a straight line. Therefore, if we follow your line back from the earth to the sun, we hit the bigger sun. This means that your star would be invisible—not because it is behind the sun, but because the sun is behind your vector, drowning it out. Or, in a total eclipse, your vector would be incident with the moon."
I admit that it is a difficult situation to construct in your head, but these scientists are wrong. They have not done a thorough study of the diagram or the problem. Imagine we are studying the problem at a total eclipse, and have our telescope trained on the edge of the sun. We photograph the star just beyond the edge of the sun. We know it is a star that should not be there. According to our charts, it should be behind the sun. So far, so good. But now we have to analyze the operation of photographing the star. The light that has developed our photograph is coming from the star and the sun. The light from both travels the same speed and covers the distance from the sun to the earth in the same time. Therefore, our photograph is a photograph of the starlight just as it passes the sun. We are looking at a situation that existed in the vicinity of the sun around eight minutes ago. Therefore, all we know is that eight minutes ago, the light from the star was just wide of the edge of the sun, seen from the earth.
If this is true, then my opponents have no argument. If you follow the line back from the earth to the sun in my diagram, as they did, you do not hit the sun at t2, you hit the sun at t1—the smaller sun. This is because as you follow the line away from the earth, you must go back in time a bit. When you reach the sun, you are eight minutes in the past: t1 is eight minutes in the past; t2 is when the light hits the photographic plate. Therefore my starlight is not drowned out by the sun anymore than theirs is. Nor is it within the eclipse.
It is at this point in my explanation that I recognized a flaw. If the sun is eight minutes in the past on a photographic plate, then all our measurements of the sun must be eight minutes old. Specifically, when we measure the optical width of the sun to determine its size, we are measuring a sun that is eight minutes old. Therefore, when we used our star charts to determine which stars should be obscured by the sun, we were using a sun that was eight minutes old there, too. And this means that we cannot go eight minutes in the past in order to find a smaller sun—one we can make our starlight pass in a straight line. We are already in the past, regarding all current measurements on the sun. The sun may be expanding, but if so, it is expanding after our photograph was taken. Its expansion thereby cannot be part of our data in this problem.
It might appear that I am beaten, but there is another body expanding in this problem: the earth. If the earth is expanding at 9.8 m/s2, then after eight minutes it will have moved over a million meters in every direction.
s = at2/2
= [(9.8 m/s2)(499s)2]/2
= 1,220,105m
At t1, the time the photograph was taken of the eclipse, the earth was represented by the smaller circle and would have been blocked from the light of the star unless it was bent. But at t2, eight minutes later, the right side of the earth will have moved far enough to the right to capture the starlight with no bend.
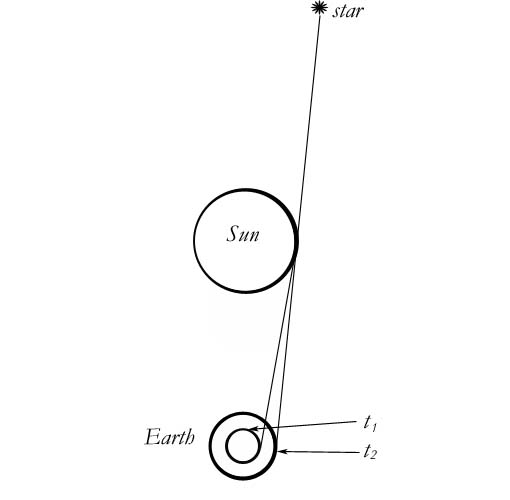
This means that it is the expansion of the earth that is responsible for the appearance of aberration, not the expansion of the sun.
Notice that I am using Einstein's theory to surpass him. I need relativity to make my new theory possible. It is relativity that allowed me to notice that the time of the sun and the time of the earth are not equivalent. A distance separation implies a necessary time separation. The fact that our photographic plate of the eclipse is a picture of the vicinity of the sun eight minutes ago is crucial to my solution. That eight minute gap allows the earth to expand enough to capture starlight that it is not predicted to be able to capture. The prediction fails because it was based on an earth that was the same size at t1 and t2.
This explanation allows me to make a very important prediction of my own. Eddington confirmed Einstein’s prediction only because his telescope was positioned on the correct side of the earth. You can see from my second diagram that only the right side of the earth would be in a position to capture the starlight. In fact, a telescope positioned on the left side of the earth looking at a star on the right side of the sun would find just the opposite “bending”. Rather than seeing stars it was predicted not to see, it would not see stars it was predicted to see. The sun would seem to be blocking even more starlight than it should. And a telescope positioned in the middle of the earth would see the sun blocking (almost) exactly what it was predicted to be, since that position would benefit least from the expansion of the earth during the eight minutes. I encourage astronomers to put this prediction to the test during an eclipse, comparing the aberration from different positions on earth. If expansion theory is true, then they will see very different outcomes from what current theory predicts.
In fact, I can provide a number for my prediction, using very simple math. I can use my number above for the expansion of the earth in 499 seconds to calculate a maximum apparent bending. We must correct the number 499 a bit in order to fit it into the calculation. The light from the star would intersect the sun at a tangent, therefore we must add the radius of the sun to the distance to the sun in order to find the length of that line. Which gives us an extra 2 seconds for the light to reach the earth. Which changes our expansion of the earth to: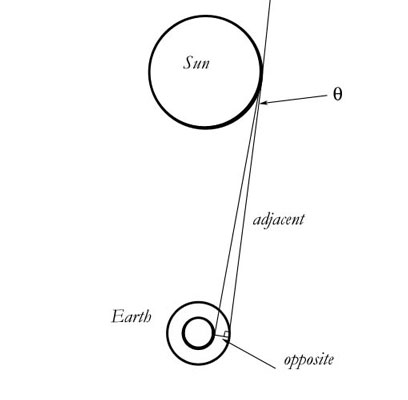
s = at2/2
= [(9.78 m/s2)(501s)2]/2
= 1,230,000m
Now, if the telescope is positioned on the earth as far right in my diagram as it can go, then the angle at the sun would be:
tanθ = 1,230,000m/1.51 x 1011m
θ
= 1.68 seconds of arc
[To see why this number does not match the current number 1.75, go here. I show that gamma causes the current equations to fail. The number 1.75 is an outcome of the current equations, not of the newest measurements.]
Telescopes positioned further toward the middle of the earth would find less bending, and telescopes on the left side of the earth would find stars obscured that shouldn't even be obscured by the solar disk.
Notice that I have found a number that is absurdly close to Einstein's first number (1.7s) without General Relativity or Newton. It makes one wonder if Einstein's numbers were not finessed in order to match the math I have done above. My math is simple and straightforward and does not require any curved fields, transforms, or tensors. It does not require non-Euclidean geometry or a host of new assumptions. It only requires applying the number for the gravity of the earth to a real acceleration of the earth outwards. You can see for yourself how blindingly easy the calculation is.
In comparison, let us look at Einstein’s math. In 1911, he provided this equation in his paper On the Influence of Gravitation on the Propagation of Light:
a = (1/c2)∫(kM/r2)(cosθds)
where the integral is taken from θ = π/2 to θ = -π/2.
Unfortunately, this equation gave him .83 arc seconds, a number that history has conveniently forgotten.
In 1916, in The Foundation of the General Theory of Relativity, Einstein got serious with his math. He gave us this equation:
B = ∫(∂γ/∂x1)(dx2)
Where the integral is taken from +∞ to -∞, and
γ = √(-g44/g22)
So we have an integral of partial derivatives, one of which is the transform gamma expressed as the square root of the negative ratio of two tensors. From all this Einstein gets the number 1.7 arc seconds.
I get the same number from this equation:
θ = tan-1(gt2/2)/d
Where g is the acceleration of the earth and d is the distance to the sun. You tell me which equation you would rather teach to students, or supply a full derivation for, or develop a theory to contain. The so-called free data in Einstein’s equations is considerable. There isn’t a speck of free data in my equation. My "field strength" is 100%.
No doubt you will say you would prefer to teach an equation that is correct. But even if expansion theory is not true, it is highly interesting to see that the correct number can be achieved in such a direct manner. In my first paper on General Relativity, I stated that the Gaussian fields were unnecessary to the theory. I said that whatever physical form the field actually took, one could construct a Euclidean sub-field beneath it in which to do simpler math. This means that even if the actual physical field is non-Euclidean, the math does not have to match the field. Modern mathematicians have been famous for claiming that you can apply any math you want to a problem, as long as you do it in the right way. And they are correct. Minkowski answered his critics by saying that his fields were a mathematical convenience: he did not need to prove their physical reality, he only needed to get the right answer. In this, he was right. Any math that does not contain false postulates is as good as any other math.** But modern mathematicians have used this as an excuse for test-driving all sorts of esoteric maths. I turn the tables on them by showing a simple algebraic solution, in a Euclidean field, that undercuts their tensor calculus.
All I have done to achieve my solution is reverse the acceleration vector of gravity. This creates a square flat field and allows me to do all my math in a simple way. Once I achieve my final number, I am then free to leave the field as it is or to take it back to the way it was. If I believe in expansion theory, then I leave the vector pointing out from the center of the earth in this problem. If I believe in Newton or Einstein and want to return to a curved field, then I reverse the vector and take it back to pointing at the center of the earth. This changes my theory but does not affect the math at all, as you can see. I have proved my claim from my earlier paper: I have solved a complex problem of curvature—a problem that Einstein used tensors to solve—without Gaussian coordinates.
A Prediction for Jupiter
My prediction above is so broad that it doesn’t have to wait for an eclipse. It can be decided tomorrow by pointing a large telescope at Jupiter and comparing starlight on the left side to starlight on the right side. Jupiter is 2097 light seconds away from earth, which gives the earth more than four times as long to expand. Let’s predict a maximum aberration:
θ = tan-1(gt2/2)/d
= 7 seconds of arc
This is a major deviation from Einstein, since he predicted .02 seconds of arc for Jupiter, based on the gravity of Jupiter. I have dismissed the gravity of Jupiter as a consideration, requiring only the distance to Jupiter from the earth. This means that we should be able to see way around Jupiter, provided that we take our picture off the right edge of Jupiter from the right side of the earth. If we take a picture off the left edge of Jupiter from the same telescope, we will find many stars obscured that should not be. An additional 7 seconds of arc (roughly—the tangent there will not be exactly 180 degrees from our first tangent, but close enough) should be obscured by the left edge.
Of course, the number 7 seconds of arc applies only when the earth is closest to Jupiter. I have used 4.2AU as the distance to Jupiter, which is the earth's nearest pass (roughly). Even greater apparent aberration could be achieved by placing earth at different positions relative to Jupiter. Let us put the earth sideways to the sun, for instance, and do the math.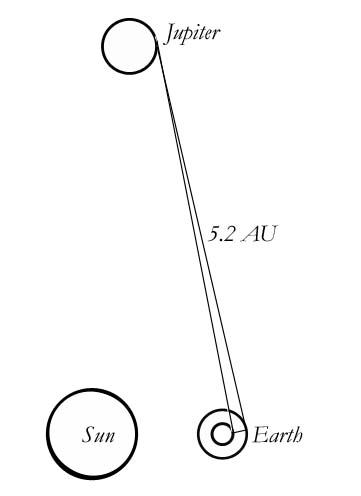
tanθ = 3.3 x 107m/7.80071 x 1011m
θ = 8.76 seconds of arc
Positions of the earth much further than this away from Jupiter will not be experimentally feasible, since Jupiter will be up only during the day.
From my diagram, it is clear that viewings of Jupiter (or the solar eclipse) must be done as close to the horizon as possible. Only in this way can the astronomer be sure that he is positioned as far to the edge of the earth, relative to Jupiter, as possible. I am aware that this brings other factors into play, but it is unavoidable.
As one final peculiarity of the experiment, notice that the scientist will actually be studying the top and bottom edges of Jupiter, as he sees it on the horizon, not the left and right edges. I have positioned the telescope on the far right edge of the earth relative to Jupiter, in my diagram. But if we imagine a little man standing on the earth at that position, his head must be pointing due right also. If we rotate the whole diagram so that he is standing up like we are, then he will be studying the top and bottom edges of Jupiter as he sees it. The top edge will give him the number for theta above, allowing him to see around Jupiter a bit; the bottom edge will obscure stars that he expects to see.
The experimental difficulties of this viewing would make it unlikely to yield results, except that there is such a huge difference from edge to edge. Also notice that it can be measured from the same location—we don’t need to travel or to compare data from different telescopes. And it doesn’t even require great precision. The clumsiest measurements will show a variation from side to side, if it exists as I predict. Seven or eight seconds of arc can be seen by medium sized telescopes, even on the horizon, provided the location and atmospheric conditions are optimal. The only thing that takes special care is in choosing the location. A telescope positioned near the middle of the earth, relative to Jupiter, will show almost no aberration and therefore almost no variation.
Now that we have thoroughly explored this problem both mathematically and theoretically, we are in a position to see why Einstein’s prediction has never been completely verified by data from eclipses. After Einstein’s fame had already been achieved by Eddington, Eddington’s method was called into question. It was found that he had pushed his data strongly in the direction of Einstein. New experiments in the 20’s and 30’s failed to verify the number 1.7, and all experiments since have been inconclusive. It is now easy to see why. Given the current explanation of aberration, scientists have not expected that the position on earth of their telescopes was important, except as regards normal considerations like clarity. They never factored in what I have shown must be the main consideration, if my theory is true. Different positions on earth must give us radically different numbers, from +θ on one edge to zero in the middle to –θ on the other edge. The variation in Eddington’s numbers at the two different locations can now be explained as (mainly) a difference in longitude. Brazil and the west coast of Africa are about 30o apart, and could not possibly see the same aberration.
As I have already pointed out, the expansion of both the sun and the earth is not as counterintuitive as it first seems. Most of us already accept the fact that the universe as a whole is expanding. Due to redshifts it is generally accepted that on large scales, objects like galaxies are fleeing one another. We accept macro-expansion. Furthermore, it is commonly believed that the center of the universe is everywhere. If this is true, it implies that expansion is not just going on "out there," billions of miles away. It is going on right here, in our own solar system. And macro-expansion implies micro-expansion. Large areas are made up of small areas. Large areas can hardly expand without the expansion of the small areas they contain. Therefore absolute expansion—or the expansion of the universe at all levels—should not be so difficult to accept. It would be more surprising, I think, if the universe were only expanding at a macro-level. That would require a greater explanation than expansion regardless of scale.
Most physicists will reply that it is assumed that the Big Bang is the cause of macro-expansion. Micro-expansion has not been seriously considered because up to now it was thought that at smaller scales gravity had caused clumping. That is, within galaxies, and especially within solar systems, Hubble-type redshifts had been overcome long ago. In order to create smaller structures like galaxies, the initial Big Bang explosion has had to be overcome somehow. Galaxies fleeing eachother, or other larger redshifts, are just leftover expansion that gravity could not touch.
All of this is pretty much unexamined theory, though. No one but Dirac, that I know of, ever hypothesized absolute expansion, and he never tied it to gravity. The feasibility of micro-expansion—within existing matter—has never been put to the test. Besides, micro-expansion does not really contradict current cosmological theory, as a whole. As a cosmological mechanism, micro-expansion works in precisely the same way as gravity, as you see. It clumps. The great qualitative difference is that it implies that there is a continual "banging" in the universe. The Big Bang was not a one-time event, in the past. It is happening right now. Every point in the universe, or at least those inhabited by matter, is expanding spherically.
Beyond this, I have already reminded the reader that current theory contains an expansion theory, although it does not tie it to existing matter. Einstein’s Lambda is an expansion of space, an expansion that is now being assigned by various theoretical physicists to new types of matter. Einstein never proposed a mechanism for the expansion of space—using it mainly as a fudge factor—and newer theory also has no mechanism. Even the avant garde theories like string theory do not explain how their new particles, strings of particles, or relationships create the space expansion given to Lambda.
Those who do not believe in the Big Bang will say that my analogy to large-scale expansions may fail, but even if it does, this failure will not much affect me. It is convenient to tie micro-expansion to macro-expansion, but this connection is not a necessary one. A universe that is not expanding at the macro-level only tells us that galaxies are not fleeing one another. Galaxies can be in equilibrium with or without the expansion of matter. You could even theorize a shrinking universe with expanding matter. The expansion of matter fits equally well into any known cosmological theory. Every theory contains some equation for gravity. Expansion is just a different explanation of the genesis of that equation, not a different final number. My theory is explained in a single step: turn the acceleration vector (due to gravity) around. Once you do that, you will still have to explain why galaxies do or do not flee one another.
In summation, you will have noticed that according to my theory, light is not bent. Its aberration is only apparent. Gravity is a motion, not a force field, so that it cannot affect the path of light. Therefore light must always travel in a straight line. In one sense this brings us back to Newton. In many other ways, you will have seen that I have gone well beyond both Newton and Einstein. Neither man had the theoretical stomach for the real expansion of matter. I doubt that Newton ever seriously toyed with the idea. I suspect that Einstein did, but he preferred to give an expansion to space. Space expansion is just avant garde enough and esoteric enough to slip under the radar, especially if you tag it with Λ or "the cosmological constant". But the expansion of matter, which implies the expansion of the earth, was too avant even for Einstein. You can steal a man’s watch, but beware of stealing the ground beneath his feet. He may applaud the former as a miracle of prestidigitation; he will likely find the latter a sacrilege.
Go to my Experiment on the Outer Planets where I show how I proved that my theory here is true.
Gravity at the Quantum Level
The (claimed) zero size of gravity at the quantum level is more proof of my theory. We are told that at the quantum level, the size of gravity is on the order of 10-40. But this is not strictly true. This number is arrived at by a complex calculation that takes into account the strength of gravity at the macrolevel and the relative size of the quantum level. But empirically, no interaction of gravity at the quantum level has ever been found. In experiment, there is no gravity at the quantum level.
We are told that this is because 10-40 is so very small. We would have to be able to measure to an accuracy of something like 34 decimal places in order to be able to discover it relative to other forces at that level. But of course our inability to measure it might also be explained by the fact that it is not there in the form we expect.
In part 2 of this series on the Third Wave, I showed that the atomic orbit was explained by a combination of the acceleration of the mass of the nucleus and electron outward and by charge. I have replaced gravity by the acceleration of mass, so you can see that gravity is there at the quantum level, in some form. But notice that in my theory it is not a force. It is motion.
Currently the orbit is explained completely in terms of charge. If either gravity or expansion is a partial cause of the orbit, then its effect will be unseen by current theory.
Current theory finds no gravity at the quantum level because it is looking in the wrong place. It proposes that the nucleus is somehow attracting the electron, despite using the E/M field, which is an exclusionary field. Current theory cannot explain the mechanism of this attraction (with an exchange of particles, for instance), but if the electron is attracted to the nucleus by charge, then there will be no use for any other “force” to create the field. In short, by trying to explain the orbit only with charge, current theory has overlooked the place of gravity at the quantum level. Gravity at the quantum level exists in the form I have given it—as a real expansion outward of both the nucleus and the electron.
In the final analysis, my theory says that the expansion of mass exists at all levels, but it exists most fundamentally, and most simply, at the quantum level. This would put an analogue of gravity at the quantum level. But, this analogue of gravity is not a force. Therefore it does not require any unification with other forces or fields, at least not in the way that was previously thought.
As the basic motion in the universe, it intersects the E/M field and all other known and unknown fields. Only in this way can it be unified with other interactions. I have already shown in this series of papers that at the quantum level it combines with the E/M field to create the orbit. In subsequent papers I have shown that the strong force can be replaced by gravity at the quantum level, and that the acceleration of gravity at the quantum level can be calculated from known numbers, giving us a field that is actually 1022 more powerful than now thought.
In fact, let us now calculate the force due to acceleration of mass, and see if it is of a proper size to fit the strong force. Here is the value I calculated for the proton:
a = 6.06 x 10-13m/s2
F = ma = 1 x 10-39v4
At first this seems way too low for the strong force, and would appear to be proportional to macro-gravity. It is what is predicted by current theory for gravity at the quantum level, and does not begin to explain the strong force as predicted by QCD. However, the reason that the strong force is thought to be so strong is that it has to overcome the electric force. But I have proposed that nucleons don’t have any E/M exclusion inside the nucleus, due to the way protons and neutrons stack. If this is true, then the strong force would not have to overcome it.
You will say, "But this contradicts the charge on the nucleus. You cannot turn off the E/M field to get rid of the strong force and then turn it back on to explain the charge on the nucleus." Yes I can, as long as I propose that the E/M field of the nucleus is external to the nucleus. The E/M field does not permeate the inner spaces of the nucleus. The nucleus repels the electron, it does not repel itself. Protons in a nucleus do not repel eachother or nearby neutrons. Their joint field sets up around them. The spins of the individual protons and neutrons do not create radiation within the nucleus; only the summed spins create radiation and therefore the E/M field, which field surrounds but does not penetrate the nucleus. This is quite easy to propose and diagram, as you can see by following the last link.
The Perihelion of Mercury
Since I accept the basic postulates of both Special and General Relativity (other than curved space), I also accept the explanation of the precession of the perihelion of Mercury. I have shown that gamma is incorrect, due to mathematical mistakes in derivation. But I have derived new transforms that are very close in output, so that it is not necessary for me to do a mathematical analysis of the Mercury problem here. Once again Einstein’s math is overly complex and slightly flawed in some places, but he (nearly) obtains the correct final answer. It is therefore pointless to use this problem as a theoretical difference between current theory and my gravitational theory. There is no difference between my theory and Einstein’s regarding the cause of the precession of the perihelion of Mercury. Einstein accepts a centripetal vector, or its mathematical equivalent, so that you can, if you desire, apply the tensor calculus to my field just as you do with Einstein’s field. The only difference is the genesis of the centripetal component of the tensor. Turning the acceleration vector around does nothing to the mathematical field by itself, as Einstein admits with the equivalence principle. Later I will show some small variations between the two maths, but they are caused by specific mathematical operations, not by a difference in theory. What I mean is that, as in the case of gamma, I am forced to correct some strictly technical errors of current math. But this does not conceptually impact the Mercury question, so I will not get into it here. [To see a full mathematical and mechanical analysis of the perihelion of Mercury, go here. It is worth reading, since I show a 4% error in the field equations of the Sun, as well as a nearly 90% error in the actual amount of precession (80 instead of 43).]
Levels in an E/M Field
I will now be asked to explain why the different planets exist at different distances from the sun. So far I have acted as if an orbiting body were sitting on the bubble of an E/M field. But we have eight or nine planets and thousands of other objects in the solar system, all orbiting at different levels. How can I explain this using the E/M field as the main generator of exclusion?
I will limit myself to a broad answer here, and a suggestion for further research. I don’t feel compelled to give a precise answer, since current theory has no precise answer for this that I must compete with. Using gravity as the sole generator of orbits, current theorists cannot begin to explain why the planets have the orbital distances they do. I can do a bit better than that, at least. I take the orbits of electrons as my pattern. Quantum scientists accept that electron orbits are caused entirely by the E/M field, and they also accept that multiple levels are achieved. If they accept this at the quantum level, I do not see that it is any more difficult to accept at the macro-level.
I would suggest that an orbiting body is affected by all orbiting bodies beneath it and above it. Therefore, to build the solar system, we would need to know which orbits formed first. These bodies will create E/M patterns that future bodies entering the system must conform to.
Chance plays a part, as current theory also believes. A major cause of orbital distance is probably the distance a new body happens to intersect the solar field.
Where my theory departs most from current orbital theory is in the suggestion that orbital relationships can best be understood by looking at the intersecting E/M fields. The first field to study in this regard would be the field of the moon. I suggested in a previous paper that the orbital distance of the moon was not an accident based on initial trajectory or speed, but that it could be explained as a function of the E/M field of the moon and of the earth. If this is true, then it applies to all other orbits as well, planetary as well as those of satellites. For instance, Mercury and the smaller planets can exist in nearer E/M shells to the sun, for the simple reason that they are excluded less strongly. Jupiter and Saturn must orbit at greater distances simply because their own E/M fields are bigger. We add the exclusionary force of the sun to the exclusionary force of the planet in order to get a first approximation of the orbit.
[I have now done the math explaining the orbital distance of Mercury as the conjunction of the E/M field with the gravitational field].
[I have now also done the math explaining Bode's Law in full.]
Of course other factors must be considered. In the case of Uranus and Neptune, I think we have planets intersecting the solar field after the stabilization of Jupiter and Saturn. Their orbital distance is therefore not determined only by the field of the sun. If they had predated Jupiter, they would have settled lower than him. As it is their orbital distances are determined by an additive field of sun+Jupiter+Saturn. Uranus and Neptune aren’t orbiting the sun as much as they are orbiting the trio. Newer small planets suffer the same fate. They cannot find a place under Jupiter, so they accumulate only above Neptune, in various levels of the Kuiper belt.
But again, I do not think it is necessary for me to explain the form of the solar system, since no current theory claims to be able to do so. It is undeniable that an E/M field allows for various levels of orbit. And it is undeniable that a study of intersecting E/M fields should help to explain the motions of bodies within those fields. It is my belief that the E/M fields within the solar system are a much richer source of information on orbital distances than so-called gravitational fields. The “field” created by expansion in my theory constrains all orbits on the outside, but almost all other relationships are explained by the strengths of the E/M fields at work.
*It is now most commonly called bending or deflection of starlight, but I call it aberration, since I will show that is what it is.
**Minkowski’s math contains several false postulates, as I show elsewhere. It contains the false postulates of Einstein (like x = ct) and it adds to them the false postulate that time travels at a right angle to x, y, z.
Click here to go to Part VI of the Third Wave
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.