Where R is Rydberg's constant,

Every decade, basic physics and mechanics is plowed under by more and more needless math.

Feynman's question should have been, what is the relationship of the electron's mass to its charge, or what is the relationship of the electron's energy to the photon's energy. He and his colleagues couldn't answer these questions because they had already buried them under so much math, but I can answer them quite easily. To do that, we first have to dig Planck's constant out of the rubble and show what it really is.

---

If we go to the Wikipedia page on Planck's constant and scroll down to the section called “origin of Planck's constant,” we find that Planck himself had no idea of the value of the constant. He was working, like Newton before him, with proportions. In looking at Wien's displacement law, Planck proposed that the energy of the light was proportional to its frequency, and then simply made up the equality with his constant. In other words, he had no idea where the constant was coming from. Planck did not develop the equation from mechanics, he developed it from experiment: specifically, the experiments at the turn of the century on black body radiation.

That Planck had no idea where his constant was coming from is understandable, but that later physicists could not figure it out is beyond belief, especially after Einstein gave them the equation E=mc². Planck's constant is now taught as a conversion factor between phase (in cycles) and action. But action is an old feint: a longstanding blanket over mechanics. So we can ignore that. The constant is expressed in eV seconds, erg seconds, or Joule seconds, all of which are unhelpful mechanically, so we can ignore them as well.

I will now show that Planck's constant is very easy to derive mechanically, which makes it astonishing that the derivation is not on the Wiki page or in any textbooks. Once you see how easy it is, you will agree that this information must be hidden on purpose. There is no way that a century of particle physicists could have been ignorant of what I am about to prove, so we must assume they were hiding it with full intent to deceive.

We take Einstein's famous equation and apply it straight to the photon. We don't need the transform gamma: gamma applies to everything except light. Light is a special case, remember? Einstein's postulate 2? So we can apply the equation as is, with no transform.

E = mc²

c = λν

E = m( λν)²

h = m λ²ν

Now, take a common photon like the infrared photon, with a wavelength of about 8 x 10^-6 m. In that case λ²ν = 2,400. So,

h = m(2,400)

Planck's constant is about 2,400 times the mass of the photon.

You will say, “But the photon doesn't have mass!” And I say, that is what they want you to think, which is why they never use Einstein's equation on photons. Giving the photon mass, or even a strict mass equivalence, would bring down the entire structure of QED, so they can't let you go there.

You will reply, “But your math is just circular. You haven't explained anything mechanically.”

Not yet I haven't—in this paper—but I send you to my paper on photon motion, where I develop a mass for the photon without using Einstein's equation. I will do it again here. We start with the difference between the mass of the electron and the mass of the nucleon, which is called a Dalton, and which is about 1821. I have already shown that this number comes from the stacked spins on the electron, and I developed an equation that yields not only the Dalton but all the meson levels as well. In other words, I gave a mechanical explanation of the number 1821, with simple math and simple motions. In the paper after that, I showed that this same quantum equation will give us the photon mass as well, by assuming the photon inhabits a fundamental level of the equation, just like the electron, nucleon, and all the mesons. This fundamental level is 1821³ beneath the proton level, or 1821² beneath the electron level. All we have to do is multiply the proton mass by 1/1821³, which gives us:

1.67 x 10^-27(1/1821)³ = 2.77 x 10^-37 kg

That is the mass of the photon, derived without Einstein's equation. So my math is not circular.

But is it the correct math? Let's see. If we multiply that mass by 2,400 we get 6.63 x 10^-34 kg, which is, sure enough, the number value of Planck's constant.

I have proved my point. Planck's constant is hiding the mass of the photon.

But how does this answer Feynman's question? We have to go back to the fine structure constant and remove all the fudge.

α = 2πke²/hc

I have shown in other papers that k and π are ghosts, and in this paper I have shown that h and α are ghosts, so we have to dump them. We will use their numerical value to absorb them into the equation.

e² = hcα/2πk = 2400mc(.0073)/5.65 x 10¹⁰ = .091m

e = .3√m

e = 1.602 x 10^-19 C

1C = 2 x 10^-7 kg/s (see definition of Ampere to find this number in the mainstream)

e = 3.204 x 10^-26 kg/s

e = 6.08 x 10^-8[√kg)/s](√m)

So, Feynman's question becomes “How do we explain this numerical relationship of m to e?” Well, we can't do it from these equations, as you now see, since these equations are not giving us a number relation between m and e. They are giving us a number relation between m and e². To get the right dimensions for e, the dimensions for that last constant must be √kg)/s. Since there is not a 1-to-1 relationship between s and √kg, even that last number is not telling us what we want to know.

We have more work to do. Let's look first at that number for e in the next to the last equation, which is the current one. I have expressed it in kg/s, and this brings a lot of things to light. Remember that the electron has a mass of 9.11 x 10^-31 kg. According to this equation the electron is emitting a charge every second that outweighs it by 35,000 times. The electron is emitting the mass equivalent of 35,000 electrons every second, or 1.16 x 10¹¹ photons per second. So it is not just my charge field that has mass. The standard model charge field has a huge mass, it is just hidden by these dimensions like the Coulomb. Ask yourself why the standard model and textbooks never write the fundamental charge as kg/s. Textbooks tell you that charge is mediated by virtual photons, but they don't tell you that the electron emits 35,000 times its own mass of these virtual photons every second, just to create charge. You see, if they told you this, they would have to field your next question, which is, “How can the electron emit so much mass and not dissolve? How does this conserve energy?” In my theory, I put that question out in the open and try to answer it, but the standard model prefers to dodge it with all their sloppy math and undefined constants and complex dimensions like the Coulomb and Ampere and Volt. [Go to my papers on Galactic Rotation and the Bullet Cluster to see how I use this math to solve longstanding problems in astronomy.]

What allows us to solve this easily is the loss of the constant k. Remember that I said k is a scaling constant, and we don't need it here. The reason is because in these equations we are comparing quanta to eachother: no scaling is involved. For the same reason, we can import a trick I used in my quantum gravity paper, where I showed that as long as we are staying at the quantum level, and not scaling, we can use a very familiar number for gravity at the quantum level. If we are measuring gravity at the quantum level from our level, then we have to scale down using the radius as the scaling transform. But if we are not scaling, we can use 9.8 m/s² as the number for gravity. I showed that if the quanta measure their own gravity, this is the number they would get. It sounds crazy, I know, but I will show how it works again here. We just find a unified field force for the proton, using its mass and its acceleration.

F = ma = (1.673 x 10^-27 kg)9.8 m/s² = 1.639 x 10^-26 N

Multiplying by two to represent the vector meeting of the fields of both electron and proton gives us 3.279 x 10^-26 N. Amazingly close to our bolded number above for e, isn't it?

You will say “Yes, but you have a pretty significant difference, 7.5 x 10^-28 N. You also have the wrong dimensions. The elementary charge is in kg/s, and your number is in N.”

Let's look at my margin of error, first. If we divide, we find my error is about 2.3%. But I have already shown in my papers on the Bohr magneton and Millikan's oil drop experiment that the Earth's charge field is skewing all experiments done on the Earth. It is responsible for the .1% difference between the Bohr magneton and the magnetic moment of the electron. It was responsible for Millikan's error. And so it must also be responsible for a .1% error in computing quantum masses. The proton's mass is determined in experiments done here on the Earth, and physicists have never included the effect of the Earth's charge field, since they don't know it exists.

You will say, “Your error is 2%, not .1%”. First of all, it is not my error: it is the standard model's error. And the error enters this problem in multiple places. Just as in Millikan's oil drop experiment, we have a confluence of errors. Let's look at the mass spectrometer, used to “weigh” the proton:



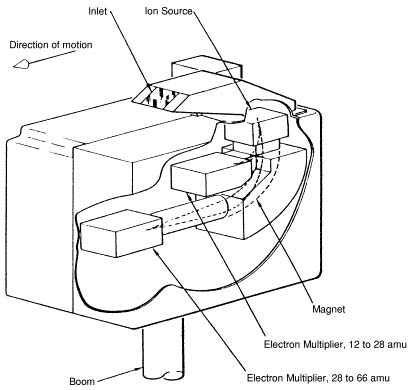
As you can see, the spectrometer must suffer the same problems as the oil drop experiment, since the magnet is in the plane of the Earth's charge field. The ions are moving straight down to start with and have a downward vector throughout the experiment. This can't work. The magnetic field is also rather weak, so it has no chance of burying the error simply by field strength

But even if the machine is turned 90^o, so that all motion is horizontal instead of vertical, the problem will remain. Unlike Venus, the Earth is both electrical and magnetic. If the experiment is done vertically, the electrical field of the Earth interacts. If the experiment is done horizontally, the magnetic field interacts. Both fields have the same strength, as produced by the charge field, so you are damned either way.

Although the mass spectrometer, either horizontal or vertical, must encounter the Earth's charge field, it does not encounter it precisely like the oil drop experiment did. Millikan set up the his electrical field in vector opposition to the gravity field, and included gravity in his calculations. But the math of the mass spectrometer attempts to ignore gravity, as an experimental constant. Masses in mass spectrometers are not calculated from gravity (in the experiment), they are calculated relative to eachother. Wikipedia admits that “there is no direct method for measuring the mass of the electron at rest,”² and this is also true of the proton. You can see that the proton must be moving in the spectrometer, and its path must be bent by a field. The relative bend then tells us the mass.

At any rate, gravity is present throughout the experiment, and though it can be ignored as a matter of relative mass, it cannot be ignored mechanically. Because it is present, it must be included in any correction. Both it and the induced magnetic field are affected, but because they are not in vector opposition we don't treat them the same as we did with Millikan. With Millikan, we applied the charge field correction directly to his electrical field, since he aligned them. Here we halve the correction and then take the square root to square the effect. We halve the correction because the motion of the particle in the curve goes from (nearly) all gravity to (nearly) all induced magnetic field. Look at the curve in the diagram. At the end of the path, the particle is not moving down at all. So we go from “gravity is the entire cause of motion” to “gravity is almost no cause of the motion.” If we sum that path, from all to none, all being 1 and none being 0, then the average will be about ½, given a smooth curve. So we only get half our error during the experiment. We only get half of it, but we still have to take the square root, since the error affects both the gravitational field and the induced magnetic field. Two effects will give us an increased total effect.

The charge field of the Earth is .009545 m/s², which is .0974% of gravity. Half that is .000487, and the square root is .0221 or 2.21%. Above, my error was 2.3%, so I am now within .0009. The rest of that error is probably due to my math alone, since, as a theoretician, I almost never carry my calculations past the thousandths place. I will let those who love precision fine tune my math.

Now let's look at the dimensions. I have a force; the standard model Coulomb reduces to kg/s or Ns/m. But remember that the standard model is not too picky about its dimensions. The cgs system is still used, and in that system charge was kg or Ns²/m. Yes, before SI, charge used to reduce to mass, although they never promoted that fact. So the dimension changes with the system. It changes again with my system, so that charge is a force, not a mass. I can change the dimensions without changing the number, because s/m reduces to one in my mechanics. Charge is the mass of the photon field, but a mass cannot give us a strength of interaction or a force by itself. You need a mass and a velocity, as I have shown elsewhere. This will give you a field strength, which will give you a force. Well, velocity is m/s. If you multiply s/m by m/s, you get one, and the field dimension reduces to N.

---

But what does all this mean for the fine structure constant? It means that the number for the fine structure constant comes from misusing Coulomb's constant in quantum equations. In the equations we looked at above, k should never be used, so the defining equations for the fine structure constant are just garbage. The only way to understand what the fine structure constant is, is to look at the impact parameter equation of the Rutherford formula. If you take that link you will see that the fine structure constant is just a transform or scaling constant between mass and charge. Mass and charge have been defined in two different ways, by two different sets of field equations, but they are actually equivalent. The fine structure constant just takes us from one to the other. But again, if we didn't have the constant k fouling up field equations at the quantum level, we wouldn't need the fine structure constant at all. My own unified field equations rewrite all charge as mass, jettisoning the redundant field equations of charge. Of course this allows me to jettison k and the fine structure constant as well. That is what I showed you above, by finding the correct numbers using Newton's equations like F=ma instead of electrostatic or quantum field equations. To make the unified field equations completely mechanical and transparent, we have to jettison all mention of the old charge equations, since they weren't mechanical. All classical and quantum E/M equations quickly devolve or dissolve into virtual fudges and finesses, and I have swept all of that out the door forever. All E/M field theory, quantum and macro, has to be rewritten in terms of volume, density, and real particles with real size, and that is what I have done.

---

Conclusion: The elementary charge is not a charge, it is a unified field force. The standard model believes that forces at the planetary or astral level are all gravitational and at the quantum level are all E/M, but this is false. The forces at all levels are unified field forces. The elementary charge includes gravity. For this reason we can use Newton's equations at the quantum level. Newton's equation is a unified field equation, and if we use it correctly, we can use it at any level. The measured masses of quanta are unified field numbers. All masses are unified field numbers, since they represent compound motions and forces. Quantum masses are hiding both fields, and this allows us to calculate “charges” straight from masses, without Coulomb's equation and without Planck's constant.

The elementary charge is not only a unified field force, it is a compound of emission by both the electron and the proton. Even when we are measuring the charge of the electron alone, the field will be composed of proton and electron emission. You cannot study electron charge alone, or proton charge alone, since you cannot go anywhere in the universe where the charge field is unipolar. Even on the surface of the proton or electron, you will find a bi-polar field. The charge field is everywhere, and it its strength is everywhere determined by compound emissions.

For the record, this is also why you can't have a magnetic monopole in the real world. There are no walls: the charge field is everywhere, and it is everywhere created by both protons and electrons (and anti-protons and positrons).

For a different and slightly simpler explanation of where the fine structure constant comes from, you may also consult my paper on Rutherford's scattering equations, where I show that the atomic world is about 137 times larger than we think.

For a more recent update on the fine structure constant, you can read my newest paper, where I show that the fine structure constant is a mass to charge transform, and tie it to other important charge numbers.

¹QED, p. 129.
²http://en.wikipedia.org/wiki/Planck%27s_constant

---

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.