|
|
return to
homepage
return to updates
How
my Unified Field solves
the Galactic Rotation Problem
and
how the dark matter math is fudged
by
Miles Mathis
Abstract:
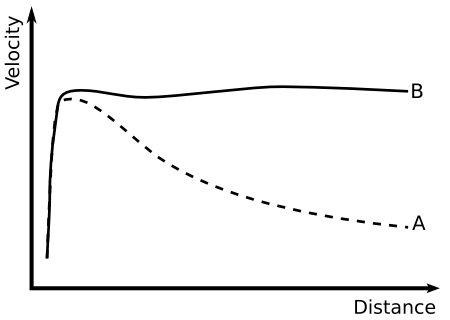
I show that in addressing the Galactic Rotation Curve, MOND is a
hint in the right direction, despite being only an added
function. I show that my unified field fills in all the holes of
MOND. Then I show the gigantic fudge in the math of the dark
matter hypothesis. Adding mass cannot solve galactic rotation,
except by magically redefining Newton's variables. Then I show
the unified field equation for velocity that solves the entire
problem, in one line of math. Finally, I show why "normal"
matter is only 5% of the total, deriving the 19 to 1 ratio by
simple math, directly from current equations.
In
a long paper on the Allais
Effect, I mentioned several modified Newtonian fields of the
past, including those of Quirino Majorana and others. Once we are
familiar with these older (and failed) modified Newtonian fields,
we can see the newest modified field in the same light. I am
speaking of course of MOND, the Modified Newtonian Dynamics of
Mordehai Milgrom [from about 1983]. While this MOND is preferable
to the theory of dark matter, and while it does move slowly in
the right direction, it is woefully incomplete (as I think even
Milgrom would admit). Lee Smolin has put it this way:
MOND
is a tantalizing mystery, but not one that can be solved now.
He
means by that that MOND seems to point to some new field, but
that it is not a field we know about. Smolin is both right and
wrong. MOND is tantalizing, in that it implies a new field; but
the mystery has already been solved: the “new field” is
simply the charge field. MOND is pointing directly at my unified
field.
The problem is that Milgrom's new function μ is
physically and mechanically unassigned. It is basically just a
fudge factor or a hole filler, a piece of raw math with no
theoretical or field underpinning. In other words, we are never
told what causes it.
The form of Milgrom's math is also a
clear problem, since, like Majorana and the others before him, he
adds the field outside of Newton's equation. In MOND, the
rotational velocity is found by this equation
v = 4√GMa0
As you see, his
constant is separate from G and M.
But I have shown that
Newton's equation is correct, as written. This is why I do not
call my unified field a modification of Newton. I have not
modified Newton's equation, I have pulled it apart and
interpreted it more fully. You see, the trick is that the
necessary variations are already contained within G and M, so we
do not need any new functions or constants. We just have to
understand what G and M really stand for, and how they work
mechanically.
This is why the solution has been so
difficult to see. It was hidden in the constants and variables we
already had.
Let me gloss my
unified field one more time. The
Universal Gravitational Constant G is the key, since it is
not a naked constant, but a scaling constant between two fields.
Newton's equation, as written, already contains the charge field,
and G scales between charge and gravity. All we have to do is
write each mass in the equation as a density and a volume, giving
the volume to the gravity field and the density to the charge
field. G then scales between them, taking the atomic size down to
the photon size. This is necessary because gravity is
relationship between atoms, or things made of atoms, while charge
is relationship between photons and atoms. For charge to work,
photons have to collide with atoms or ions, and this requires a
scaling between the two particle sizes. I explain this much more
fully elsewhere.
Once Newton's equation is interpreted in
this way, we find subtle changes in the field. I have already
uncovered many of these changes in
other papers [see especially the two-mile problem], but in
this case the change becomes quite large and obvious. The
velocity divergence in outer arms of galaxies is very large, and
is not what anyone would call subtle. This is why I found this
problem so interesting, and why I had to leap on it instantly. It
is solved immediately not by tweaking the equation, but by
recognizing the variation in the field. Put simply, the charge
field variation from center of galaxy to outer reaches is very
large. Since all matter emits charge, there will be much more
charge near the center of the galaxy.
The mainstream has
missed this obvious field variation for many reasons. One, they
give charge to the messenger photon, which is a virtual photon.
Since virtual photons do not take up any space in the field, they
could not provide any drag. Two, even if they began giving the
charge field to real photons, their real photons also do not take
up any space in the field. Since they are point particles in the
math, they cannot take up space or provide drag in the field.
Three, all mainstream theories have ignored the charge field
completely. They have tried to solve this problem with gravity
alone, or gravity plus relativity, or gravity plus unassigned
functions. They have not seen that Newton's equation must include
the charge field. Nor have they seen that if Newton's equation
includes the charge field, it must cause both subtle and unsubtle
variations in the field mechanics.
I will be told that my
solution requires more than just a re-interpretation of Newton's
equation. It also requires a re-interpretation of the photon.
Newton's equation, by itself, has nothing to say about the
photon. True enough. However, it may be worth pointing out that
Newton did not think the photon to be virtual or to be a point.
He agreed with me since he agreed with Descartes on this
question: anything that exists has extension. The photon exists,
therefore it must have a radius. If it has a radius, it takes up
space. If it takes up space, it must provide drag.
The
mainstream should know this, since they admit that the photon has
momentum and energy. A thing with energy and momentum could
hardly be “invisible” in the field. It could not act as a
ghost, regarding drag. A photon could not be capable of knocking
electrons out of atoms, but incapable of taking up space in the
field. A mathematical point cannot knock an electron out of an
atom. This is because scattering could be thought of as a kind of
drag. Both would be caused by real collisions. You cannot propose
that the same particle can cause scattering, but cannot cause
drag.
The reason Milgrom's MOND was so tantalizing is
that he had the right variation, in a way, and also the right
explanation of it. He said that his function did not cause
measurable variation in the solar system because gravity is so
strong here, near the Sun. That is not precisely correct, but it
is a good hint. It is not because gravity is so strong here, it
is because the Sun is the only major body acting as the central
mass, making the velocity follow the inverse of the radius (see
below).
This is why the solar system seems to follow
gravity alone, while the galaxy seems to follow charge. The
unified field relates gravity to charge, and this makes Milgrom
nearly correct. The density variation in the solar system acts to
diminish the charge field variations due to the sphere, causing
the bodies to follow classical equations pretty closely. This is
just one more reason charge has been invisible to us.
This
is also why globular clusters show much less charge variation,
and therefore much more velocity variance, than galaxies. It is
simply a matter of density distribution. Globular clusters are
known to have much higher star densities than galaxies, and, as
with the solar system, this density tends to flatten out the
charge variation. Less charge variation means greater velocity
variation, as we will see in the equations below.
But
first, let us look at the dark matter hypothesis for a moment.
Initially, it was said that around 50% of the matter of a galaxy
must be in a galactic halo, completely outside the visible
galaxy. This number is now about 95%. Yes, a big problem required
a big solution, and this tells us how large the velocity variance
from prediction really was. I should think the theory has long
since gone past the point of absurdity, just based on that
percentage, but I will look more closely at it anyway. If you
visit a place like Wikipedia, you find dark matter proposed as
the solution to velocity variance, but you get no math or theory.
How does dark matter in the halo, even at 95%, cause a flat
velocity? If the answer were clear, you would think Wikipedia
would take the time to gloss it. It shouldn't take long, should
it? This is a big clue. Wiki usually likes to cloak the theories
with math, but here we get nothing. That must mean the math is
really pathetic.
You only have to do the baldest math to
see that extra mass out there can't solve the problem. Remember,
the mainstream math doesn't have my charge field, so they are not
using charge to flatten the field as I will. They are adding mass
but not charge. If you simply add mass to a halo, you cannot
increase an orbital velocity. This is because orbital velocity
has nothing to do with mass. It has to do only with distance from
center. a = v2/r,
remember? No mass variable there. The dark matter hypothesis is
not any type of MOND, so it is not claiming to modify Newton at
all. Well, according to Newton's equations, the orbital velocity
is determined by distance and nothing else. Jupiter's orbital
velocity is not determined by its mass, and if we took the Earth
out to the distance of Jupiter, it should have the same orbital
velocity as Jupiter.
The dark matter hypothesis needs to
tell us more than “dark matter.” It needs to tell us how dark
matter can cause greater orbital velocities. Say there is
a huge amount of dark matter
in a halo around most galaxies. How will this affect the velocity
of shining matter that we can measure? Well, it would tend to
suck all the matter out of the galaxy toward the halo, but it
wouldn't affect the orbital velocity of that matter at all
(unless it decreased it—see below). This is because, according
to both Newton and Einstein, gravity has no force at the tangent.
A gravity field cannot apply a tangential force, only a
centripetal force. Therefore, a large halo could only pull out on
matter inside it. It could not pull sideways. According to both
Newton and Einstein, gravity can neither cause nor increase a
tangential
velocity. It has no mechanism
to do so. According to the explicit math of Newton, an orbital
velocity is the compound of a centripetal force of gravity and an
innate motion of the orbiter—this innate motion being the
tangential or straight-line velocity. Since gravity and the
innate motion are independent, gravity can never affect the
innate motion. Therefore gravity cannot cause the tangential
velocity, much less change it. It can only determine the radius,
given the innate velocity.
The mainstream* try to get
around this by using this equation
v2
= MG/r
Whereby, if you
increase the mass you increase the velocity. Unfortunately, that
is gigantic fudge, since M is the mass of the center, not the
mass of some body in orbit. That equation comes from solving
these three equations
F = ma
F = GMm/r2
a
= v2/r
M is explicitly defined as the large central mass causing
the field, not the mass in orbit. In the case of a galaxy, it
would be the mass of the galactic core, not the mass of the
galaxy as a whole or of a body orbiting the galactic core.
Therefore, their math is completely upside down. They have
“solved” only by ignoring the explicit definitions of the
variables in the equations. At the Duke University website linked
below, the author states
M
= mass lying within
stellar orbit
That
proves my point, since that means we are talking about the
galactic core here. Since the core is not a discrete object in a
galaxy, all the mass inside the radius can be called the core. M
is the central mass, not the orbiting mass. This is crucial,
since the mass and the velocity both increase as r increases. An
increase in M doesn't just increase velocity in the outer
reaches, it increases velocity everywhere proportionally, like an
increase of a.
To say this another way, the dark matter
people want to re-interpret Newton in a very unorthodox way. They
want to take my sentence, "the mass and the velocity both
increase as r increases" and interpret it to mean that if we
add more mass at radius r, we can increase the velocity at that
distance. So they do just that. They add more and more mass as
the radius increases, to force this mass to offset the normal
workings of Newton's equations. Unfortunately, that is not what
Newton's variable assignments and equations tell us. M in the
equation above does not stand for mass at that radius, it stands
for mass inside
that radius, as Duke
University admits. This makes the velocity at all radii greater,
but does not make the velocity at all radii equal.
This
means that the dark matter math is also a type of modified
Newtonian dynamics. It is modified in that it takes the
definitions and turns them upside down. We could call it a FFAND:
a falsified and fudged Newtonian dynamics.
What this
equation of Newton v2
= MG/r is actually telling us
is that if we increase the mass of the galactic core, we can
increase all the orbital velocities, at all radii. But it is not
telling us that we can flatten the field in any way. And if we
increase the mass of a halo, we have thereby relatively decreased
the mass of the core, which must DECREASE all orbital velocities.
Dark matter would make the problem worse.
Another major
problem with the dark matter solution here is that a halo with
that amount of matter could not remain undetectable in
our own galaxy. We
always hear of dark matter supposedly found here and there, as
WIMPs or whatnot, but of course the best place to look would be
in our own halo, would it not? If 95% of the mass of the galaxy
is in a halo, then it cannot be invisible to all detection, dark
or not. Remember, we are in an outer arm of our galaxy, and
therefore we would be quite near this halo. Unless we are looking
toward the core, we are looking through this halo whenever we aim
our telescopes into space. With a mass nearly equal to the entire
galaxy, this halo must have an appreciable density. Why doesn't
it affect our extra-galactic views? We can't detect it even
indirectly, as it shifts or distorts or tamps down incoming data.
It doesn't really matter if it is baryonic or non-baryonic: if it
is real, it must have density, no matter what it is made of. It
cannot have mass and lack density, can it? A thing can have mass
and lack density only by changing the definition of mass or
density. That is what all the larking about with non-baryonic
matter is: the attempt to convince you, by some sort of
speechifying, that matter can have mass but no density. WIMPs and
axions and hidden sector particles are all "heavy"
particles with no density. They are heavy ghost particles, in
other words. If you can imagine heavy ghosts, good luck to you.
The fact is, "heavy" and "weakly interacting"
are mutually exclusive adjectives. A thing can interact weakly
only if it is small or diffuse, and if it is small or diffuse, it
cannot be heavy. Once more, this is just the sad attempt to
change the definitions of words. As the void is now a thing, and
as virtual particles now cause motions, we have heavy massive
particles that are both weakly interacting and undetectable. It
is so pathetic it truly defies belief.
I believe in some
dark matter. The earth is a bit of dark matter, of course. But
these theories of weakly interacting massive particles could not
be more silly. The fact that anyone takes them seriously is a
sign of the nadir. We don't need WIMPs, we need to understand
that photons have mass and radius. All these ridiculous problems
and theories are caused by refusing to let the photon be a real
particle.
Remember that I have shown that charge
is equivalent to mass. But the standard model has not gotten
that message. They have forgotten to weigh all the charge in the
universe and to include it in their energy totals. They don't
even include the weight of the E/M spectrum in their totals,
telling us that photons have no rest mass. In other words, they
don't include the mass of visible photons, much less the mass of
invisible photons that we already know about, like infrared
photons and so on. The few models that do include normal photons
in the mass of the universe only include a small fraction of
them. For instance, I
have shown that every proton is emitting a charge each second
that outweighs it by 35,000 times (see math below). All that
charge is unweighed by the standard model, and is not included in
their totals. That is why they need dark matter and dark energy
in the amount of 95%. Dark energy is mostly charge. It is charge
photons. This charge is also what is causing drag in the inner
parts of the galaxy, creating a flat velocity line.
With
this under out belts, we can return to the MOND equation for
velocity.
v = 4√GMa0
Once
again the problem is with the mass variable M. Milgrom created
MOND to compete with the dark matter math, but he accepted their
definition of M. The fudge I uncovered at Duke has been embedded
in the galactic rotation problem almost from the beginning.
Milgrom does not use a capital M here by accident. He just took
their math and varied it, using his new functions and constants,
as is clear from this equation. Therefore, he has inherited their
fudge. His mass is misdefined, so that his equation cannot prove
what he hopes to prove. Because his mass M is the mass of the
central body (galactic core, in this case), his equation is
flawed at the ground level. An increase in that mass will
increase the velocity, yes, but it will not flatten the graph. It
will increase all velocities proportionally. To do what he wants
it to do, the mass would have to be re-assigned, as with the dark
matter math. But you cannot do that without cheating. To do that
would not be a modification of Newton, it would be a complete
refutation of Newton and his variables.
The form of
Milgrom's equation also makes it impossible for him to solve this
problem. As you will see from my math, what we need is a
differential, but Milgrom's velocity equation is too simple. Both
G and a0 are constants, so that v can be a constant
only if M is. But M cannot be a constant, as we saw with the dark
matter math. M is the core, which in a galaxy is anything below
radius r. This means that as we increase r, we increase M. So M
is changing in Milgrom's equation. This means that v will also
change, and the velocity is not flat.
On the other hand,
if Milgrom defines M as the mass of a constant core, he is guilty
of another cheat. He has rigged his equations so that the radius
cancels, which means we don't know the radius for the velocity he
is finding. He simply states that the equation is good for all
radii, but his derivation doesn't show that. To the contrary, his
equation requires a radius, and it is saved in the current
form (to a small degree) only because mass will vary as radius
does. If he redefines the mass as a constant, however, he has
just contradicted his own derivation.
So
let me now correct all this bad math and theory. As a first
question, we may ask how dense the matter field, and therefore
the charge field, would have to be in order to begin causing
photon drag. Well, we know that the charge field is dense enough
in the solar system to cause axial
tilts and variations from Bode's
law and perturbations and torques and magnetospheres
and so on, so the charge field here is already dense enough to
cause drag. All charge field phenomena could be called drags of
one sort or another, and if the charge field can cause
perturbations it can cause velocity variances. It is not lack of
a charge field in the solar system that causes the planets'
velocities to follow the inverse of the radius, it is something
else entirely, as I show below. Therefore, a matter density such
as we find in the vicinity of Neptune is more than enough to
create the required photon density. If it were not, then the axis
of Neptune could not be turned by the charge field.
[Addendum,
June 2015. I have been told in response to this paper that
photons have no drag. But that is now known to be false. Yes, it
has been predicted that photons have no drag, and that has been
taught for decades—mainly to protect the gauge math. But the
mainstream is now being forced to admit that photons do have
drag. See this
recent experiment reported at Phys.org confirming it.]
But
again, how dense is the charge field? I
have shown that the proton is emitting about 35,000 times its
own mass every second as charge. You will say, "Hold on
there! I won't bother taking that link, since that is
ridiculous." But I took it right out of current
definitions:
e
= 1.602 x 10-19
C
1C = 2 x 10-7
kg/s (see definition of Ampere
to find this number in the mainstream)
e
= 3.204 x 10-26
kg/s
If the proton is
given a charge of e,
that's 35,000 electrons masses per second. And it comes out to 19
protons per second. If
the charge photon has an average mass of around 2.77 x
10-37kg,
then that is around 1.15 x 1011
photons per second. 11.5
billion photons per second, by each charged baryon. Which is an
average density of .03 kg/m3/s
inside the Bohr radius. We will make good use of that density in
later papers.
So why don't we measure the charge field
when we weigh things? Because the charge field is completely
uncontained and cannot be weighed. It is traveling c in all
directions, and has no rest mass. Despite that, its mass must be
included in all totals. If standard model totals are correct, and
95% of the total mass is unaccounted for, then it would appear
that photons outweigh everything else by about 19 to 1. After
doing the math above, that is not hard to believe at all. In
fact, the math just above generates the number 19. That is why
the mainstream is getting a figure of 95%: 95% is the same as 19
to 1. Current physicists have the right number but the wrong
explanation. It is the charge field that outweighs baryonic
matter by 19 to 1, not dark matter.
Some have read these
equations and dismissed the 19 to 1 ratio as a coincidence, since
my equations include a time variable. But it is no coincidence.
My exposition of these equations shows exactly how mass is
already time dependent itself. Since I have shown elsewhere that
mass is actually a motion, mass must also be time dependent.
Motion is always time "dependent," since time is in the
denominator. This would mean that nothing is really time
independent. Another way to say that is that the current 19 to 1
ratio of "dark matter/energy" to baryonic mass already
includes a time variable, without anyone being aware of it. Since
the time variable always used is the second, my new equations
match the numbers of mainstream equations. The only difference is
that my equations include the second explicitly, and theirs
include it implicitly. Since the charge field is an emission
field, it has to include time. Not that time varies as we move
from past to future, but that emission is a thing that happens
over time. Emission is a process, not a static fact. That is why
my equations include the second. The mainstream equations don't
include the second, because they are equations of mass or charge,
and it is thought that mass and charge are static when they are
not. They may be STABLE, but they are not static. Mass and charge
are both motion, and all motion includes time, by definition.
Some will say, "That implies that the mass of the
proton is not really measured in kilograms, it is measured in
kilograms per second. You can't mean that." Yes, I do mean
that. The current notation is fine in most circumstances, since
we drop the time in almost all equations. It only comes up in
problems like this, when we see clearly that charge is an
emission, and an emission happens over time. That is clear
enough, I think, but since I have shown that mass and charge are
dimensionally the same (and always have been, in mainstream
equations), if charge is time dependent, mass must be also. For
more on this, reread my paper
on charge, especially where I show why charge is sometimes
expressed as mass and sometimes as mass per second.
All that
was an interesting diversion, but we don't need to count up
photons or weigh them in order to solve this problem. We can take
some shortcuts, the biggest shortcut being G. We know that if the
charge field drag is ignored or if it is constant, a spherical
field can be simplified to v = √(ar). But let's rewrite that to
get a mass in it
F = GmM0/r2
F
= ma
a = GM0/r2
v
= √(GM0/r)
That mass is the central mass, or the mass inside the
radius r. If we let M0
be the mass of the entire
galaxy and r equal the radius of the entire galaxy, that equation
gives us a velocity of about 390 km/s for stars at the edge our
own galaxy, which is close to the current value of 220 km/s. But
this remaining difference indicates appreciable charge field drag
even at the outer edge of the galaxy. It also indicates that the
current numbers are wrong, since we don't have enough mass in the
outer reaches to make up that much difference.
But now we
have to include the charge field drag, to create a differential
equation. In the above equation, we have the charge field
included in the scaler G, so that the equation is already a
unified field equation, but we have not indicated a charge
presence in the field as size, so that the photons can create
drag. As written, the equation only indicates the energy of the
charge field relative to the gravity field, allowing the charge
field to collide with matter and create the E/M field. But the
equation does not include the separate but related ability of the
charge field to create resistance or drag. To do that, we have to
create a separate term in the equation, and subtract it from the
first term. Like this:
v
= √[(GM0/r)
– (Gmr/r)]
This second mass is
defined as the mass at radius r, rather than the mass inside
radius r. This solves the problem of previous maths, which did
not include both variables. This second term represents the
density of the charge field at a given radius and allows us
subtract it out as a sort of drag. Because the mass at that
radius is multiplied by G, it becomes the emitted charge field
instead of the matter field. In the first term, G scales between
two fields, both fields being represented in the term. But in the
second term, G is simply taking the matter field and turning it
into the charge field. In this way, the second term is able to
represent the drag of that field. Many would have tried to solve
by creating a drag equation, but this is a much simpler method of
solving, as you can see.
Once we study the equation, it
becomes clear why it gives us different slopes for the galaxy and
for the solar system. This equation is actually the correct one
for all systems, but in the solar system we approximate by
ignoring the second term. If you insert some numbers, you find
that the reason it doesn't create a flat line in the solar system
is that the mass inside r is always about the same. With only
small variations, the mass inside r is just the mass of the Sun.
So M0
doesn't change with different
values of r, and this makes v change with r inversely. But in the
galaxy, M0
changes greatly with different
values of r. All the mass inside r counts as the core, so it
increases substantially as r increases. And as the first term
gets larger, the second does too, which means the differential
tends to remain nearly constant due to the density distribution
of spiral galaxies.
Some will say that this new equation
can't be right, since it gives us too large a variance in the
second term for planets in the solar system. And if we apply the
equation to the orbit of the Moon about the Earth, the variance
becomes even larger. Am I really offering this equation as a
general equation? Yes, I am, since these problems are easy to
solve. First of all, the variance isn't that great, due to the
square root, even with the Moon. And we also have other factors
we are ignoring. Remember, in the solar system and Moon system,
we have a charge field inside
a greater charge field. In the
case of the Moon, for instance, the equation would be existing
inside the much greater equation of the Sun's field. The Sun's
charge field is much greater than that of the Earth, so it tends
to tamp down the charge variations between the Earth and Moon.
This also applies to the solar system, since the solar system is
not only in its own charge field, it is in the greater charge
field of the galaxy. Nonetheless, this new equation will help us
fine tune all the velocities in all orbits. It will also force us
to recognize the field presence of the photon, not only as charge
but as resistance. This is the correct equation, and always has
been. Historical and current equations are only attempts to
derive this full unified field equation.
Yes, this is my
relativistic unified
field equation, in its velocity form. In an earlier paper, I
developed the relativistic unified field equation, as a force, by
a completely different method. Here, I developed the velocity
equation from first postulates again, not using my UFT force
equation. Fortunately, the two equations match, confirming both
papers and both equations. You may study an even
more recent paper to show how the two equations resolve.
Now, the form
of my new equation is crucial, and it should look familiar to
you. As a differential, it should look similar to the Lagrangian.
In fact, it is just a variant and corrected form of the
Lagrangian, solving for v instead of L (energy). In
other papers I have proved that the Lagrangian is already a
Unified Field Equation and that it has always included the charge
field. So to solve this Galactic Rotation Problem, physicists
should have applied the Lagrangian to it, rather than the
equations they did. But even if they had thought to do that, they
could not have applied it in the correct way, since they don't
understand what the Lagrangian really is or how it can be used.
Because they believe the T term is kinetic energy, they
completely misunderstand the mechanics buried beneath the
Lagrangian. But the T term in the Lagrangian only mimics the form
of kinetic energy. In reality, it is neither kinetic nor
potential. Nor does it stand for the charge field or the EM
field. Both terms in the Lagrangian are and always have been
unified, with the T term being a correction to or extension of
the other term. The V term is Newton's gravity equation,
which—though roughly correct in most uses—is actually
incomplete as a field equation. The T term completes the field
equation, basically expressing the variation caused by the size
incompatibility between the charge field and the matter field.
Along with the scaler G, it allows us to combine both fields in
one Unified Field Equation, expressed as a differential.
Other
critics will point out that we have done experiments showing that
photons coming to us from long distances are not affected by any
ether, field, or "foaminess" of space. NASA recently
published a video
showing just this, in a long anticipated experiment. Shouldn't
this disprove my equation and my theory? No, since the photon
field is not affecting photons in this paper. The photon field is
affecting matter here. I am proposing that photons have drag on
matter, not that they have drag on other photons. I have never
proposed that the charge field affects the linear speed of
photons, or that it would affect small wavelengths more than
large wavelengths. I have shown that it would change wavelengths,
but not that it would change some more than others. Therefore,
the NASA experiment and other experiments have nothing to say
here.
From all this, we see that the problem has been
that contemporary physicists do not understand Newton's gravity
field. They don't even comprehend the variable assignments, and
nothing is more basic. I have shown that this applies to both
sides of this argument. It also applies to the non-symmetric
gravitational theory of John Moffat, since Moffat just tries to
hide behind tensors, and the conformal gravity of Philip
Mannheim, who hides behind Riemannian curves. We do not need
curved math or tensors to solve this. We just need to understand
the variables and constants in Newton's equation.
Conclusion:
we do not have to propose any modification to Newton or Einstein
to solve the galactic rotation problem. Nor do we need dark
matter. We simply have to recognize the charge field, which
already resides inside Newton's equation. Once we do this, the
problem evaporates.
Addendum: I am told that the bullet
cluster killed MOND and proved dark matter, but I have now
published a
refutation of the Clowe et. al. papers from 2004 and 2006
that all refer to when saying this. In it, I show that once again
bad math, poor logic, and unproved assumptions are standing in
for real physics.
Postscript, September 2011: my editor
Joe Hyde just sent me this
link from University of California Santa Cruz and the
Institute for Theoretical Physics Zurich, where they are claiming
to have finally modeled a spiral galaxy. This was considered
impossible before now, since using the current gravitational
theory they couldn't get enough mass into the arms. They solved
it by using three supercomputers, including NASA's Pleiades
computer, on which alone they logged 1.4 million processor hours!
This was just part of over nine
months of
"number crunching". This is supposed to impress the
reader, but I remind you of a little thing called Occam's razor,
which they like to trot out whenever it suits them (and hide
whenever it suits them). Look above, where I solved the same
problem in one day, in my head. It doesn't require "number
crunching", as you see, or any number of supercomputers. It
requires a minor correction to the old faulty equations. Not a
push, but an actual correction. The difference between a push and
correction is that the push has no theory attached, only reams of
computer paper. My correction above includes all the mechanics,
as usual, since I show you the physical cause of each
mathematical step. They didn't need a lot more fancy math or
computer time, they needed to recognize that the charge field
existed inside their gravity equations. As I have shown, their
own equations—which go back centuries—were already telling
them this.
Postscript 2, October, 2011: Those who have
proposed charge or electromagnetic solutions to cosmological
problems have been shouted down for almost a century, assured by
the mainstream that E/M plays no part in the math of celestial
mechanics. Unfortunately, data from their own colleagues has long
conflicted with this assurance, and it is conflicting louder and
more often with each passing year. As just one example, I send
you to this new paper [ArXiv**
and AjP] by researchers at Los Alamos National Laboratory, who
have obtained “for the first time, a direct determination of a
galactic-scale electric current (~ 3 × 1018
A) , and its direction away
from the AGN. Our analysis strongly supports a model where the
jet energy flow is mainly electromagnetic.”
*http://www.phy.duke.edu/courses/055/syllabus/lecture24.pdf,
p.4
**http://aps.arxiv.org/PS_cache/arxiv/pdf/1106/1106.1397v2.pdf
If this paper
was useful to you in any way, please consider donating a dollar
(or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me
to continue writing these "unpublishable" things. Don't
be confused by paying Melisa Smith--that is just one of my many
noms de plume. If you are a Paypal user, there is no fee;
so it might be worth your while to become one. Otherwise they
will rob us 33 cents for each transaction.
|