return to homepage
return to updates
An Update on Weight
in which I falsify F=GMm/R2
by Miles Mathis
Abstract: In the first part, I show in more detail how my compound field works mechanically to create mass and weight. This solves a few problems left over from Part VII of my gravity papers. In the second part, I use a new thought problem to pose a question neither Newton nor Einstein has answered, or can answer. In answering it, I show that F=GMm/R2 is incomplete; that in certain situations it is, in fact, false: it gets the wrong answer. In compressing two fields into one equation, Newton unknowingly left certain information out of this equation, and this information is needed to solve a specific set of problems in dynamics.
In Part VII of my Third Wave papers, I spent some time talking about weight, but a clever reader may have found an apparent inconsistency there (I haven’t actually gotten any complaints, so hopefully no one has noticed this so far except me). There and in many other places I define the total force field, and therefore weight, as a differential of two fields. Specifically, I have shown that Newton's equation is a compound equation, comprised of two fields. The problem is that in this expanded equation, I have put the two fields in vector opposition. That is to say, taken together, the gravitational vector points in and the E/M vector points out. This appears at first to be a problem, since I state outright that the E/M field is a bombarding field. It causes a real repulsion. If this is so, then my lead cube in the example in that paper should actually weigh less than the empty cardboard box. The two are the same size, so according to my new theory they should have the same gravitational field. And the lead cube is emitting a much denser foundational E/M field, therefore it should propel itself away from the Earth. If it does so, it would seem it must weigh less, in the unified field of the Earth.
As an apparent confirmation of this contradiction, I state in my second paper on G that a denser Earth would cause objects on it to weigh less, not more. It would do so precisely because it is bombarding them with a denser E/M field, offsetting the apparent gravitational attraction.
Well, I stand by that assertion, concerning the denser Earth. But I have a simple explanation that resolves the apparent contradiction of the lead cube. I confirm that the lead cube has a denser bombarding field than the cardboard box, and I confirm that the force and therefore the weight of the lead cube is a function of the differential field. But I do not confirm that the lead cube should weigh less. I could hardly do that and remain sane. To resolve this, we simply have to study the meeting of the fields of the Earth and the lead cube. All things are emitting the foundational E/M field, according to my theory; therefore the Earth and lead cube must both be emitting. The problem is caused by jumping to the conclusion that the total field of the two is found by adding repulsions. That is not how it works.
We have two real fields here, made of real particles, so nothing esoteric or strange is going on. It is simple mechanics. If the two fields were able to dodge each other, then we would just add their effects together. The Earth would repulse the lead cube with a field density of x, the lead cube would repulse the Earth with a field density of y, and the total repulsion would just be x + y. But, precisely because the fields are real, they are not able to dodge each other. One is moving in one direction, which we will call z, and the other is moving in the other direction, which we will call -z. If we assume the two fields interfere, then the total repulsion will be x - y. The field of the lead cube actually tamps down the field arising from the earth. And this is precisely what we should have expected, given real particles acting in a strictly mechanical fashion.
You will say that in my recent paper on the charge field, I said that two protons must repel each other with a greater force than one proton repelling. Isn’t this another contradiction? No, since the mechanics aren’t equivalent. We must assume that two protons have equal fields, so that even with interference of the fields, we would expect a total field that was greater than either field alone. In order for this not to be true, each field would have to destroy half the other one. That would be a very dense field indeed. I am not proposing a field nearly that dense at the quantum level. But in the example here, with a lead cube on the surface of the Earth, our two fields are not equivalent. Due to surface curvature alone, we must expect the Earth’s field to be much denser than the lead cube’s field. The Earth is not as dense overall as the lead cube, but it has much more mass backing it up and less curvature to dissipate the field density. This means its E/M field density must be greater than the cube’s. Since we have a denser field meeting a less dense field, we assume the denser field will annihilate the less dense one. If we call the two fields x and y, as before, the total field at collision will actually not be x - y, it will be x - y - y. The y-field will be destroyed, and it will destroy y-amount of the x-field. But if the y-field is small compared to the x-field, then my initial equation will stand, as a limit or approximation. There won’t be much difference between x - y and x - 2y, you see.
If we now do a comparison with the cardboard box, we find the E/M field of the cardboard box is able to tamp down the field of the earth much less than the lead cube was able to. Therefore the earth levitates the cardboard box more than the lead cube. The earth is accelerating gravitationally at the lead cube and the cardboard box at the same rate, therefore the lead cube weighs more. My differential field gives us precisely the same final effect as the standard model explanation. Denser objects weigh more on the earth.
[To sum up this strange discovery: 1) a denser object in a gravitational field weighs more, but 2) a denser central object, with an unchanging radius, will create a weaker total field, and therefore less weight in objects on or near it. If, all other things being the same, we increase the density of a lead cube sitting on the Earth , it will weigh more; but if we increase the density of the Earth, the lead cube will then weigh less. A change in one object is not equivalent mathematically or theoretically or mechanically to a change in another object. This means that Newton’s equation is incomplete once again, since he never discovered this subtlety. For Newton and the current model, an increase in density of either of the two masses should and must cause a greater force of attraction.]
You will say that it is convenient that my example with the lead cube, once clarified, mirrors current expectations; but that it does not really give you any reason to prefer my explanation over the standard model. True as far as it goes in this particular example. But beyond this example, I have given hundreds of mathematical and theoretical reasons to prefer my explanation of gravity, not the least of which are the many problems I have solved with it, including assigning the value of G, the dimensions of G, the proton mass limit in accelerator, the optical size of Sun and Moon, the cause of the Metonic Cycle, the correction to the perihelion of Mercury, the correction to the bending of starlight by the planets, the explanation of planetary and satellite torques, the explanation of the lack of angular momentum in the Sun, the explanation of orbital differentials, a resolution of renormalization, an explanation of charge, an explanation of the double slit experiment, an explanation of the mass deficit, an explanation of the Allais Effect, an explanation of Cavendish, an expansion of Newton’s equation, an explanation of tides, and on and on. Even with no way to change the density of the Earth to check my latest assertion, my theory is not short of predictions, proofs, evidence, data, or math.
But even here, I can give you a reason to prefer my explanation. I have said that a denser Earth must make all objects on it weigh less, not more. This is a difficult prediction to confirm, since no one has yet developed a method for varying the density of the Earth, simply to verify “wild” statements. Beyond that, we have already landed on our twin planet, Venus, and found nothing to shock anyone regarding weight or mass, so why should anyone take my claim seriously? They should do so since the Moon already gave them cause for alarm decades ago. I will return to Venus in a moment, but let’s look at the Moon first, to show how difficult it is to shock those who aren’t paying attention.
The total force on the Moon, which we now give only to gravity, has been found to be 1/6th that of the Earth. We did not know that for sure until we landed there and measured it directly. But how do we get that number only from the known parameters, without a Moon landing? The easiest way is to multiply the radius differential and the density differential, as I showed in The Moon Gives Up a Secret. 3.67 x 1.65 = 6.05. That makes perfect sense with my unified field, since in my theory one field is a function of the radius alone and one field is a function of the density. We can get a total force differential by just multiplying them together, never worrying about a thing called mass. But given the standard model, this equation doesn’t make much sense. According to the standard model, mass is density times volume, and gravity is supposed to be a function of mass. Therefore, if we had never landed on the Moon, and we wanted to predict gravity on the Moon using standard model equations and known data, we would look at volume and density differentials. The volume of the Moon is 1/50 that of the Earth and its density is .606. Therefore we would expect its gravity to be .012 or 1/81 the gravity of the Earth. This is not what we found, but no one did me or Newton the favor of being shocked by this. They should be shocked because it means that gravity is not a function of mass. Mass is a function of volume and density, but the Moon’s gravity is a function of its radius and density. Volume and mass don’t appear to have anything to do with it. Why is no one shocked by this? It completely annihilates the assumptions of Newton and the standard model, but people accept all three and go on with their business.
A standard-model apologist will say that gravity is dependent on mass and distance, as in the equation F = GMm/R2. But that distance is a distance between objects, not a radius. The standard model elides from one to the other with no rigor, but they aren’t the same. According to that equation, radius is of no concern; but we have just seen with the Moon that radius must be of concern [more on this below].
According to my theory, even the radius and density equation is a mirage. It gets the right answer but implies the wrong mechanics. In my differential field, we get the right answer by looking at density, but not the density of the molecules in the Moon. No, to understand what is really going on, we should look at the density of the foundational E/M field on the surface of the Moon, since that is the actual cause of the mechanics. In Newton’s equation, I have shown that G is the transform that gives us the density of the foundational E/M field, given the density of the atomic or molecular field. But here I will show you another direct method.
In this method, we need only a surface area. The Moon has 1/13.22 the surface area of the Earth. So with an equal density of emitting particles, the Moon would have 13.22 times as dense a foundational E/M field. To find the total number of emitting particles in a body, we multiply the density and the volume. This also gives a thing called mass, since density times volume is mass. But in my equations, it is not the mass that this number really represents; it is the total number of emitting particles in the object. We don’t care how much each particle weighs, or a total mass, we only care how many of these particles we have emitting the E/M field. Another way to look at it is that all the particles in the object are emitting, not just the ones on the surface. So to find the emission at the surface, we divide the total emission by the surface area. This turns out to be equivalent to dividing the mass by the surface area, which gives us 81/13.2 = 6.1.
Notice that I have just solved without looking at the gravitational field. We get a force differential between the Earth and Moon (1/6) without looking at gravity at all. We look only at the force from the emitted E/M field, and we get the number 1/6 directly. We were able to solve this way, since we are finding a force over a dt, or over one defined interval. And the way I have defined gravity or expansion, we cannot have a gravitational acceleration over one interval. An acceleration requires a series of intervals. Over one interval, you can only have a velocity. In my equations above, we are not comparing velocities, we are comparing bombarding forces. These forces will certainly cause accelerations over any series of intervals, but in comparing the relative sizes of the two total fields, this was not a concern.
You will say I used the radius to find both the surface area and the volume, so I cannot say I ignored it. True, but I did not use it to compare gravitational fields. I compared E/M emission fields only, and got a force directly. In order to achieve that last number 6, I did not look at gravitational numbers at all!
You may think it is a trick, or just a coincidence concerning the Moon, but it works with Venus, too. The Earth is 1.227 times more massive than Venus, and has a surface area that is 1.109 times as great, which gives us a surface gravity of 8.86m/s on Venus, according to my equation. That is the accepted figure.
What about the other equation, density times radius? The Earth’s radius is 1.053 times that of Venus. Its density is 1.059. That gives us a surface gravity of 8.8m/s. Not an exact match, but very close.
This should continue to astonish us, both that mass over surface area is a better predictor, and that mass over surface area is equal to density times radius. Neither Newton nor Einstein nor any of the current standard model equations can account for this in any way. They can juggle equations in similar ways, yes, but they cannot tell you what is happening mechanically, in real fields with real motions. The experimental numbers we are finding in the solar system do not support the standard-model theory, since these numbers are telling us it is the radius that determines the field, not the volume. If gravity does not change as the volume, it does not change as the mass. If gravity changed as the mass, or as the volume and density, then the Moon’s gravity would be 1/81 that of the Earth. It is not, and so the standard model is once again out in the breeze.
Our apologist for the standard model would answer that I am misdirecting from the beginning, with my field comparison equation R x D = 3.67 x 1.65 = 6. He will say that the real equation used for this purpose is
g = GM/R2
That is the normal way to estimate the Moon’s gravity, “using known parameters.” And in that equation we do have a radius. I have been saying that the force wasn’t a function of radius, but here it is. It is a function of mass and radius. With a sphere, a radius automatically tells us a density. So, I will be told, in this equation we have mass, density, radius, and volume.
All true, but all not to the point. My points are all unanswered by this standard reply. First of all, I draw your attention once again to G: the standard model has never been able to say why G is there. It is completely left out of their mechanics and their theory. It stands here only as fudge factor. I have told you precisely what G is, both the number and the dimensions. I have placed it firmly in the mechanics and in the fields. Beyond that, you can see that little g varies with mass and radius squared here. Our apologist wants to divert us by showing us that radius does matter, contra my argument above. But I can turn the tables on him. In my equation R x D it makes perfect mechanical sense. Here it doesn’t. Here the acceleration is a function of radius squared. Doesn’t that seem odd to you? It should. Because what it means is that, given two objects of equal mass, the larger one will have a weaker gravitational field. And it will have a weaker gravitational field at all distances. If you are two miles from the center of object A and two miles from the center of object B, and they have the same mass, but A is bigger than B, you will move toward B.
Can the standard model explain that, using gravity as an attraction, and gravity as a function of mass? Can Einstein explain it? What curves the space: the object as a whole, or each quantum in the object? At two miles out, how does the space know the difference between the two objects? Given equal masses, the curvature at equal distances should be equal. Why isn’t it? Or, returning to Newton, same questions: how can an equal mass or an equal number of quanta create different fields at equal distances? According to this equation, you don’t just need mass; you need mass and radius. Not the distance of the second object from the center, but the radius of the central object! Even with equal central masses, and equal distances of separation, we have found unequal gravitational fields, using the last equation above.
This should also be a problem, in that it contradicts Newton’s other equation. By that I mean that g = GM/R2 contradicts F = GMm/R2. The second equation tells us that the force of attraction varies with the two masses and the distance of separation, and nothing else. The first equation tells us that the gravitational field, which is responsible for the force of attraction, varies with the mass and the radius of that mass. The second equation tells us that the radius doesn’t matter; the first tells us it does. They both cannot be correct. Applied to the same problem, one equation will give you a different answer than the other one. And yet the first was derived from the second! How is it that no one else sees this as a problem? How has this remained in the shadows for 350 years? This is not difficult math. This is high-school algebra, for pity’s sake.
Our standard model apologist will reply that g only applies to the acceleration at the surface of the gravitating object. I answer, Newton’s equation F = ma is supposed to be a general equation. In the equation F = mg, g is the real acceleration of the object, so g = a. Why can’t we use the substitution at other radii than the surface? If my two-mile example above fails, why does it fail? The standard model can’t tell us why it is true if it is true, or why it is false if it is false. One begins to doubt if they know. Neither Newton nor Einstein has any mechanics that will settle the question one way or the other, so we must rely on experiment and observation, and airy explanations after the fact. Pretty sad, after more than three centuries.
Another way to state the problem is to show that the standard model divides the equation F = GMm/R2 by m to get a = GM/R2, but defines R as distance between objects in the first equation and as the radius in the second. This is mathematically disallowed. You cannot redefine a variable in the middle of a derivation. It would be allowed only if the second equation were generalizable in the same way as the first. That is, it would be allowed only if the second equation worked for any distance. But we are told it only works on the surface of the object. We need an explanation of all this, not just rules, and the standard model doesn’t give us one. An explanation would require some mechanics, and neither Newton nor Einstein has any mechanics to offer us, only equations.
Also notice that in the equation F = GMm/R2, the distance of separation is labeled R (or r) although it is not a radius. This trick allows for the fudging when we divide by m to find a = GM/R2, and R does become a radius. Physics is full of little visual tricks like this, to keep you from asking important questions. If the distance was labeled “d” in the first equation, as it should be, then people might balk when we divide by m, and magically get a radius. As it is, no one bothers to even study it. They think, “It is in a book, and has been for centuries: why look at it?”
The standard model is damned if they do, damned if they don’t. If g does depend on radius, as in my two-mile example, then Newton’s two equations contradict each other, as I said. If g does not depend on radius, then it must depend only on mass. In which case we are back to my previous criticism. If it depends only on mass, then we should be surprised that the Moon has 1/6 the gravity of the Earth, instead of 1/81.
Instead of talking about g, let us talk about field strength at any given distance from the center. In this way we can get beyond the “only at the surface” dodge of the standard model. My entire previous criticisms, in both forms, can be boiled down to this: the standard model includes an inverse square law to match observation and data, but has no way to explain that law. It also flubs from distance to radius, with no apology except that it works. A law should be the necessary outcome of a transparent mechanics, but the inverse square law of gravity is only the outcome of observation. The law would only make sense as part of a real field, made up of real particles, but neither Newton nor Einstein has that. Neither does graviton theory, since a real field of that sort would have to explain attraction, and no possible field can explain attraction. Real fields made up of real particles can only be bombarding or repulsion fields.
I am the only one who has solved this problem mechanically, since it requires a compound field. In this compound field, we do have a real field made up of real particles, and it is a bombarding field. It creates a real repulsion. This is the E/M component of the newly expanded unified field (formerly known as the gravitational field). This part of the field explains the inverse-square nature of the compound field, since a spherical field must dissipate with distance, in a straightforward manner. The other part of the compound field is a pseudo-field created by expansion, with no mediating particle and no inverse-square law (except Relativity, see below). In this way, we have attraction and an inverse-square law, but it turns out that the inverse-square law and the attraction are separate phenomena. It is not just that Newton’s equation can be expanded into two basic motions or interactions; it is that the qualities of these motions can also be expanded and separated. It is not only the variables or the nouns that can be separated, it is the adjectives that go with the nouns. We had always thought that we were looking at a single field, and that all attributes must go to that field. But no: some attributes are qualities of one field, and some are attributes of the other. The inverse-square attribute applies to the E/M field but not the gravitational pseudo-field. An apparent attraction applies to the gravitational pseudo-field, but not to the E/M field. The E/M field is never attractive, not even between protons and electrons.
The Two-Mile Problem
Let us return to the most important visualization and thought problem in this paper, the two-mile problem from above. Let us see how my compound field solves this problem mechanically. In doing this I will be able to clarify all my arguments up to this point.
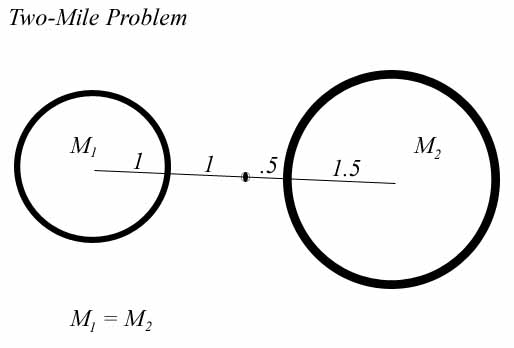
To repeat, let us say that we are two miles from the center of two objects of equal mass. One object has a radius of one mile and the other has a radius of 1.5 miles. This puts us one mile from the surface of one, and ½ mile from the surface of the other. According to Newton’s equation, we should feel equal forces from both. We cannot apply the g equation, since we are not on the surface of either one. What does my mechanics have to say about it? Since I have shown that gravity—as a solo field—is dependent on radius only, one object should be “attracting” us 50% more than the other one. As a ratio of fields strengths, gravity is dependent on radius and radius alone. But beyond the surface of the object, this gravitational acceleration must fall off, and it falls off due to Relativity. As I show in a lengthy proof in Part III of my gravity papers, all accelerations obey the inverse-square law, due to time differentials. Even linear accelerations—ones not produced by spherical bodies—diminish with the inverse-square law. This means that our larger body will be attracting us 1.5 x 22 or 6 times as much as the smaller one.
But both objects are also emitting the foundational E/M field, so we must include that also. Using the surface area and mass equation that I developed mechanically above (to find the density of the E/M field), we find the first object with a field at the surface of
M/SA = 1/4π R2 = 1/4π
and the second object with a field of
M/SA = 1/4π (1.5)2 = 1/9π
So we see that the bigger object is moving at us faster, but bombarding us less. However, we must look even closer. It is bombarding us less, but we are twice as close to it. We are ½ mile from the surface of the larger object and one mile from the surface of the smaller. Beyond the surface of the objects, the E/M field drops off by an inverse quad law, since this is a real field of dispersing particles. As such it must diminish by an inverse-square law due to the spherical shape of the field—which we can now see comes right out of the surface area equation; but it also obeys the inverse-square law of Relativity, just like the gravitational acceleration. The two together give us 1/d4. This makes the comparative field of the second object 24 x 1/9π = 16/9π. So the larger object is bombarding us 7.1 times as much as the smaller.
Can we solve with just this information? We have an attraction that is 6 times as much and a repulsion that is 7.1 times as much. But no, we can’t solve without knowing the relative strengths of the two fields. And I have shown in other papers that the relative strength of the two fields is not constant. As your objects get smaller in size, the gravitational field gets smaller but the E/M field gets larger, as a fraction of the total. With the Earth and Moon, I have shown that the gravitational field is stronger than the E/M field. With the Earth, the gravitational field is 1000 times stronger; with the Moon, it is 2.5 times stronger. But with a 1” lead ball in a Cavendish machine, it is 1.86 times less strong. So we must take the sizes of our objects into consideration, in order to solve.
Here we have objects one mile and 1.5 miles in radius, so from the previous examples, we should expect the two fields to be about equal (one mile is between 1” and 1738 km, and so the field ratio will be between 2.5 and 1/1.86 or .538). I don’t need to calculate the precise ratio here. It is enough to show that if the field strengths were exactly equal, then we would move toward the smaller object. The larger object is repulsing us more than it is attracting us, therefore we move away from it. Given equal masses, we move toward the denser object.
However, that is not a general answer. Notice that if we make our objects the mass and size of the Earth, the answer is different. Let the radius of the first object be 6378 km and the radius of the second be 9567 km. In this case the two fields do not have the same strength. On the Earth, the gravitational field is 9.816 and the E/M field is -.009545. The E/M field is therefore swamped, at any and all distances, and we look only at the gravitational field. The larger object is “attracting” us much more than the smaller, therefore we appear to move toward it. It will be repulsing us more, but that won’t matter, since the repulsive force will not play a significant part in the equations. In this case, given equal masses, we move toward the less dense object.
So you can see that the answer varies depending on the sizes of the objects. In one case we moved toward the smaller object; in the other, we moved toward the larger.
This is a direct contradiction of Newton and Einstein, since Newton’s equation completely ignores this subtlety. The equation F = GMm/R2 cannot solve these problems; or, if it does, it gets the wrong answer. According to Newton, the answer is always the same: we don’t move toward either object, since they have the same mass and we are the same distance from the centers of both. As I have shown, that is the wrong answer.
Same goes for Einstein, since Einstein only added time differentials to Newton. Einstein did not answer any of these subtle questions embedded in gravity theory. General Relativity cannot provide the distinctions I provide here, since it doesn’t have the mechanics I have. You have to have both fields in order to solve in this way, and GR doesn’t have them.
You may think my math and theory is very difficult to prove, since we cannot test the two-mile problem or anything like it. We don’t have planets or moons of equal mass we can go park between and collect data. But it would be quite easy to test my theory using only our own Moon. The standard model, using Newton’s equations (or Einstein’s), believes that the field of the Moon would be 1/81 that of the Earth, provided you were one Earth-radius out from the center of the Moon. Equal distance from center: therefore the mass determines the field, and nothing else. But this has never been tested. The Earth is so close to the Moon that we are always measuring a compound field. Combining the two fields always skews the findings, since even if the subtotals are false, the correct total will convince the engineers that they have the right equations. I say the standard model is getting the right total, but it has the wrong subtotals. I say the Moon’s field is not 1/81 that of the Earth’s, at one Earth-radius, and I have a way to prove it. Using current theory, there is no place to go where you could test my hypothesis, since gravity is not blockable. But using my fields, there is a place you could go to test this theory. Simply fly a satellite to the dark side of the Moon, in as slow an orbit as possible, at one Earth radius from the center of the Moon. Data must be taken while the Moon is totally eclipsing the Earth, from the point of view of the satellite. This means that the Moon is blocking the E/M field of the Earth. In that position, the satellite will be measuring the Moon’s field with as little interference from the Earth as possible. And in that position, the measurement will not be 1/81, I predict.
To find what it must be, we will solve as above. My gravity pseudo-field obeys the inverse square law, but only due to Relativity. So the apparent attraction at one Earth-radius will be 2.68 times 1/3.672, or .198 m/s2. The E/M field drops off with 1/d4, however, so if the distance increases by a factor of 3.67, the field will decrease by 3.674 or 181.4 times. Since I have shown in another paper that this field has an acceleration of 1.051 at the surface, at one Earth radius it will have an acceleration of .0058. We subtract that from the expansion pseudo-field to get .1924 m/s2. That is 1/50 that of the Earth, which is roughly the volume ratio, not the mass ratio.
Which is to say that the standard model believes the number will be about .12 in that situation. 9.8/81 = .12. I predict it will be almost .2.
The same applies to the Earth, of course. Let us put a satellite 1.5 Earth-radii, or 3190 km above the surface of the Earth, and calculate the total field acceleration. According to Newton and Einstein, the acceleration should be 9.806/1.52 = 4.3582. According to me, the acceleration should be 9.816/1.52 — .009545/1.54 = 4.3608. Close, but not the same. However, it is possible we are now capable of making measurements that exact at that altitude, and I recommend just this sort of test. It should be done away from the Moon, of course, preferably when the Moon is being eclipsed by the Earth, from the point of view of the satellite.
In conclusion, let us return to my first manipulation of numbers from the Moon. I showed that the Moon’s gravity could be estimated simply by multiplying the radius differential and the density differential. The standard model may call my R x D shortcut misdirection, but I can predict g of any body with it, without using G. That is more than they have ever been able to do. You would think it would be taught as basic physics, but I have never seen it. I have never seen M/SA to predict g either, although it is at least as useful and at least as transparent. My personal belief is that these things are purposely kept in the dark, to keep people from asking just the questions I am asking here. Modern physicists want you to shut up and calculate, but only if you are doing their busywork. They don’t want you taking a calculator to simple numbers from the Moon or Venus.
Let us continue to calculate, but continue to talk through the problems as well. We know that the radius differential between Earth and Moon is 3.67. Therefore, according to my theory, the gravitational differential must be 3.67. Gravity is dependent on radius and radius alone. So we have half our field right there. The other half of the field is caused by the foundational E/M field. I have shown above that over any dt, this field by itself is 1/6th that of the Earth’s. But in my paper The Moon Gives up a Secret, I show that this field creates an E/M acceleration that is 110 times stronger on the Moon than on the Earth. I also use this acceleration in my tidal papers. So which is it? 110 or 1/6? The answer is: both. Above, my method gave us an “instantaneous” field density, and over this “instant” the gravitational acceleration cannot be expressed. To get the number 110, we have to look at the field over successive intervals, to create an acceleration. Since the gravitational acceleration is proportional to radius alone, the Moon’s acceleration must be 2.68 m/s2. In one second, the Moon will expand 1.34 m. During the same second, the Earth will expand 4.9 m. In other words, the emitted E/M field must be dispersing within the expanding gravitational field. The two fields are working together, so any acceleration must take into account both motions simultaneously. The Moon’s gravitational field is expanding more slowly than the Earth’s; therefore it’s E/M field will be more compressed over one second, even if it is emitted at the same density.
To calculate the relative field density over time, we let the E/M field disperse into this new volume, created by expansion. The added volume of the Moon is just the total volume after one second minus the original volume.
[4π (1,738,000 + 1.34m)3/3] - 4π (1,738,000m)3/3 = 5.086 x 1013m3.
And we do the same with the Earth
[4π (6,378,000 + 4.9m)3/3] - 4π (6,378,000m)3/3 = 2.556 x 1015m3.
And we find this sliver of volume on the Earth is 50.26 times as large as the one on the Moon. We should have known this from the basic volume ratio of 50, but I wanted to do the full math anyway. If the volume ratio is 50, then any sub-volume ratios will also be 50, and any extra-volume ratios will also be 50. This last is because my expanding universe is expanding proportionally. Things stay the same relative size, despite gravity or expansion, so mass and volume ratios don’t change.
So, to sum up, we found above that the E/M field density on the Moon is 1/6th that of the Earth. But that density applies only to any small patch on the Moon. As a comparison figure, it is applicable only locally, not as a whole. If we want the acceleration that field creates, we must look at larger areas and larger times, since an acceleration cannot be calculated at an instant, an infinitesimal, a limit, or over one interval (length or time). If we want to do that without calculus or difficult equations, we do it as I am doing it here. We start with the local field density, we sum it out to the entire field, then we look at the volume it is filling. This gives us the relative field strength, as an acceleration.
1/6 x 13.22 x 50.26 = 110
In this way I have shown that although the local E/M field density of the Moon is 1/6th that of the Earth, this field creates an E/M acceleration in the compound field that is 110 times that of the Earth’s E/M field acceleration*.
*For more math on this problem, go to The Moon Gives up a Secret.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.